1 . 已知双曲线 过点
过点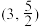 和点
和点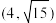 .
.
(1)求双曲线的方程.
(2)过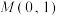 的直线与双曲线交于
的直线与双曲线交于 ,
, 两点,过双曲线的右焦点
两点,过双曲线的右焦点 且与平行的直线交双曲线于
且与平行的直线交双曲线于 ,
, 两点,试问
两点,试问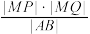 是否为定值?若是定值,求该定值;若不是定值,请说明理由.
是否为定值?若是定值,求该定值;若不是定值,请说明理由.
 过点
过点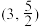 和点
和点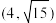 .
.(1)求双曲线的方程.
(2)过
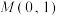 的直线与双曲线交于
的直线与双曲线交于 ,
, 两点,过双曲线的右焦点
两点,过双曲线的右焦点 且与平行的直线交双曲线于
且与平行的直线交双曲线于 ,
, 两点,试问
两点,试问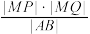 是否为定值?若是定值,求该定值;若不是定值,请说明理由.
是否为定值?若是定值,求该定值;若不是定值,请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 已知等轴双曲线C: 的左,右顶点分别为A,B,且
的左,右顶点分别为A,B,且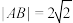 .
.
(1)求双曲线C的方程;
(2)过点 的直线l交双曲线C于D,E两点(不与A,B重合),直线AD与直线BE的交点为P,证明:点P在定直线上,并求出该定直线的方程.
的直线l交双曲线C于D,E两点(不与A,B重合),直线AD与直线BE的交点为P,证明:点P在定直线上,并求出该定直线的方程.
 的左,右顶点分别为A,B,且
的左,右顶点分别为A,B,且 .
.(1)求双曲线C的方程;
(2)过点
 的直线l交双曲线C于D,E两点(不与A,B重合),直线AD与直线BE的交点为P,证明:点P在定直线上,并求出该定直线的方程.
的直线l交双曲线C于D,E两点(不与A,B重合),直线AD与直线BE的交点为P,证明:点P在定直线上,并求出该定直线的方程.
您最近一年使用:0次
2023-10-16更新
|
608次组卷
|
4卷引用:甘肃省武威市天祝藏族自治县2023-2024学年高二上学期第二次月考(12月)数学试题
名校
解题方法
3 . 已知双曲线 的右焦点为
的右焦点为 ,且点
,且点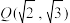 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)过点F的直线与双曲线C的右支交于A,B两点,在x轴上是否存在不与F重合的点P,使得点F到直线PA,PB的距离始终相等?若存在,求出点P的坐标;若不存在,请说明理由.
 的右焦点为
的右焦点为 ,且点
,且点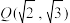 在双曲线C上.
在双曲线C上.(1)求双曲线C的方程;
(2)过点F的直线与双曲线C的右支交于A,B两点,在x轴上是否存在不与F重合的点P,使得点F到直线PA,PB的距离始终相等?若存在,求出点P的坐标;若不存在,请说明理由.
您最近一年使用:0次
2022-12-29更新
|
1349次组卷
|
9卷引用:甘肃省张掖市某重点校2022-2023学年高二下学期5月月考数学试题
甘肃省张掖市某重点校2022-2023学年高二下学期5月月考数学试题广东省部分学校2022-2023学年高三年级12月大联考数学试题河南省2022-2023年度高三模拟考试数学(文科)试题河南省2023届高三模拟考试理科数学试题辽宁省辽阳市2022-2023学年高三上学期期末数学试题湖北省襄阳市第一中学2022-2023学年高二上学期期末数学试题(已下线)专题10 圆锥曲线综合大题10种题型归类-【寒假分层作业】2024年高二数学寒假培优练(人教A版2019选择性必修第一册)专题04 双曲线15种常见考法归类(3)(已下线)专题7-4圆锥曲线五个方程型大题归类-2
名校
解题方法
4 . 已知双曲线 的右焦点
的右焦点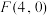 到渐近线的距离为
到渐近线的距离为 .
.
(1)求双曲线 的方程.
的方程.
(2)过点 的直线与双曲线
的直线与双曲线 的右支交于
的右支交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点 ,使得点
,使得点 到直线
到直线 的距离相等? 若存在,求出点
的距离相等? 若存在,求出点 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由.
 的右焦点
的右焦点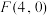 到渐近线的距离为
到渐近线的距离为 .
.(1)求双曲线
 的方程.
的方程.(2)过点
 的直线与双曲线
的直线与双曲线 的右支交于
的右支交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点 ,使得点
,使得点 到直线
到直线 的距离相等? 若存在,求出点
的距离相等? 若存在,求出点 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由.
您最近一年使用:0次
2022-10-27更新
|
1401次组卷
|
12卷引用:甘肃省兰州市第二中学2022-2023学年高三上学期第二次月考文科数学试题
甘肃省兰州市第二中学2022-2023学年高三上学期第二次月考文科数学试题湖南省部分学校2022-2023学年高三上学期10月联考数学试题广东省多校2023届高三上学期10月联考数学试题山西省三晋名校联盟2023届高三上学期阶段性(二)数学试题山西省忻州市2023届高三上学期10月联考数学试题甘肃省兰州市兰州西北中学2022-2023学年高三上学期期中数学(理科)试题河南省创新发展联盟2022-2023学年高二上学期第二次联考(期中)数学试题(已下线)第04讲 圆锥曲线综合(练)湖南省湘潭市第一中学2022-2023学年高三上学期期中数学试题辽宁省大连市第十五中学2022-2023学年高二上学期期中数学试题河北省沧衡八校联盟2022-2023学年高三上学期11月期中考试数学试题新疆维吾尔自治区喀什地区疏附县2022-2023学年高二上学期11月期中数学试题
名校
解题方法
5 . 已知F1(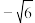 ,0),F2(
,0),F2( ,0)为双曲线C的两个焦点,点
,0)为双曲线C的两个焦点,点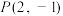 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)已知点A,B是双曲线C上异于P的两点,直线PA,PB与y轴分别相交于M,N两点,若 ,证明:直线AB过定点.
,证明:直线AB过定点.
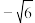 ,0),F2(
,0),F2( ,0)为双曲线C的两个焦点,点
,0)为双曲线C的两个焦点,点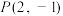 在双曲线C上.
在双曲线C上.(1)求双曲线C的方程;
(2)已知点A,B是双曲线C上异于P的两点,直线PA,PB与y轴分别相交于M,N两点,若
 ,证明:直线AB过定点.
,证明:直线AB过定点.
您最近一年使用:0次
2022-07-10更新
|
1709次组卷
|
10卷引用:甘肃省白银市靖远县第四中学2022-2023学年高二下学期6月月考数学试题
甘肃省白银市靖远县第四中学2022-2023学年高二下学期6月月考数学试题甘肃省白银市第九中学2023-2024学年高二上学期第三次月考数学试题安徽省阜阳市界首第一中学等2校2022-2023学年高二上学期11月月考数学试题广东省汕头市金山中学2024届高三上学期阶段性考试数学试题湖南省长沙市周南中学2021-2022学年高二下学期期末数学试题(已下线)专题28 双曲线(针对训练)-2023年高考一轮复习精讲精练宝典(新高考专用)(已下线)2.8直线与圆锥曲线的位置关系(1)(已下线)3.2.2 双曲线的几何性质(2)第三章 圆锥曲线的方程 讲核心03(已下线)专题3-4 双曲线大题综合10种题型归类(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)
名校
解题方法
6 . 已知双曲线
 的左顶点为
的左顶点为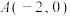 ,右焦点为F,点B在C上.当
,右焦点为F,点B在C上.当 时
时 .不垂直于x轴的直线与双曲线同一支交于P,Q两点.
.不垂直于x轴的直线与双曲线同一支交于P,Q两点.
(1)求双曲线C的标准方程;
(2)直线PQ过点F,在x轴上是否存在点N,使得x轴平分 ?若存在,求出点的N的坐标;若不存在,说明理由.
?若存在,求出点的N的坐标;若不存在,说明理由.

 的左顶点为
的左顶点为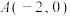 ,右焦点为F,点B在C上.当
,右焦点为F,点B在C上.当 时
时 .不垂直于x轴的直线与双曲线同一支交于P,Q两点.
.不垂直于x轴的直线与双曲线同一支交于P,Q两点.(1)求双曲线C的标准方程;
(2)直线PQ过点F,在x轴上是否存在点N,使得x轴平分
 ?若存在,求出点的N的坐标;若不存在,说明理由.
?若存在,求出点的N的坐标;若不存在,说明理由.
您最近一年使用:0次
2022-03-17更新
|
1412次组卷
|
2卷引用:甘肃省张掖市2021-2022学年高三第二次全市联考(3月)理科数学试题
名校
解题方法
7 . 已知双曲线 ,离心率为
,离心率为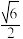 ,
, ,
, 为其左右焦点,
为其左右焦点, 为其上任一点,且满足
为其上任一点,且满足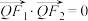 ,
, .
.
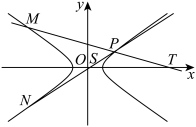
(1)求双曲线 的方程;
的方程;
(2)已知 ,
, 是双曲线
是双曲线 上关于
上关于 轴对称的两点,点
轴对称的两点,点 是
是 上异于
上异于 ,
, 的任意一点,直线
的任意一点,直线 、
、 分别交
分别交 轴于点
轴于点 、
、 ,试问:
,试问: 是否为定值,若不是定值,说明理由,若是定值,请求出定值(其中
是否为定值,若不是定值,说明理由,若是定值,请求出定值(其中 是坐标原点).
是坐标原点).
 ,离心率为
,离心率为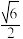 ,
, ,
, 为其左右焦点,
为其左右焦点, 为其上任一点,且满足
为其上任一点,且满足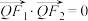 ,
, .
.
(1)求双曲线
 的方程;
的方程;(2)已知
 ,
, 是双曲线
是双曲线 上关于
上关于 轴对称的两点,点
轴对称的两点,点 是
是 上异于
上异于 ,
, 的任意一点,直线
的任意一点,直线 、
、 分别交
分别交 轴于点
轴于点 、
、 ,试问:
,试问: 是否为定值,若不是定值,说明理由,若是定值,请求出定值(其中
是否为定值,若不是定值,说明理由,若是定值,请求出定值(其中 是坐标原点).
是坐标原点).
您最近一年使用:0次
2022-02-16更新
|
858次组卷
|
3卷引用:甘肃省定西市临洮中学2023-2024学年高二上学期第三次质量检测数学试试题



