名校
解题方法
1 . 已知曲线 上一动点
上一动点 到两定点
到两定点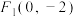 ,
,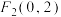 的距离之和为
的距离之和为 ,过点
,过点 的直线
的直线 与曲线
与曲线 相交于点
相交于点 ,
, .
.
(1)求曲线 的方程;
的方程;
(2)动弦 满足:
满足: ,求点
,求点 的轨迹方程;
的轨迹方程;
(3)求 的取值范围.
的取值范围.
 上一动点
上一动点 到两定点
到两定点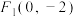 ,
,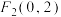 的距离之和为
的距离之和为 ,过点
,过点 的直线
的直线 与曲线
与曲线 相交于点
相交于点 ,
, .
.(1)求曲线
 的方程;
的方程;(2)动弦
 满足:
满足: ,求点
,求点 的轨迹方程;
的轨迹方程;(3)求
 的取值范围.
的取值范围.
您最近半年使用:0次
2022-09-06更新
|
376次组卷
|
2卷引用:第3章 圆锥曲线与方程 单元综合检测(难点)-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)
名校
解题方法
2 . 过椭圆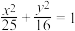 的中心任作一直线交椭圆于P,Q两点,
的中心任作一直线交椭圆于P,Q两点, ,
, 是椭圆的左、右焦点,A,B是椭圆的左、右顶点,则下列说法正确的是( )
是椭圆的左、右焦点,A,B是椭圆的左、右顶点,则下列说法正确的是( )
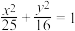 的中心任作一直线交椭圆于P,Q两点,
的中心任作一直线交椭圆于P,Q两点, ,
, 是椭圆的左、右焦点,A,B是椭圆的左、右顶点,则下列说法正确的是( )
是椭圆的左、右焦点,A,B是椭圆的左、右顶点,则下列说法正确的是( )A. 周长的最小值为18 周长的最小值为18 |
B.四边形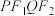 可能为矩形 可能为矩形 |
C.若直线PA斜率的取值范围是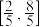 ,则直线PB斜率的取值范围是 ,则直线PB斜率的取值范围是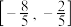 |
D. 的最小值为-1 的最小值为-1 |
您最近半年使用:0次
2022-06-14更新
|
3953次组卷
|
8卷引用:第二章 平面解析几何章末检测(能力篇)
第二章 平面解析几何章末检测(能力篇)2022年全国新高考II卷仿真模拟试卷(二)数学试题(已下线)专题27 椭圆(讲义)-2023年高考一轮复习精讲精练宝典(新高考专用)(已下线)专题23 圆锥曲线中的最值、范围问题 微点3 圆锥曲线中的最值、范围问题综合训练(已下线)考向32 椭圆(重点)湖北省潜江市园林高级中学2022-2023学年高二上学期期中数学试题贵州省铜仁市2022-2023学年高二上学期1月期末质量监测数学试题福建省福州高级中学2023-2024学年高二上学期期中考试数学试题
21-22高三上·湖南长沙·阶段练习
名校
解题方法
3 . 设椭圆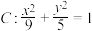 长轴的左,右顶点分别为A,B.
长轴的左,右顶点分别为A,B.
(1)若P、Q是椭圆上关于x轴对称的两点,直线 的斜率分别为
的斜率分别为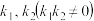 ,求
,求 的最小值;
的最小值;
(2)已知过点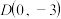 的直线l交椭圆C于M、N两个不同的点,直线
的直线l交椭圆C于M、N两个不同的点,直线 分别交y轴于点S、T,记
分别交y轴于点S、T,记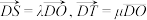 (O为坐标原点),当直线1的倾斜角
(O为坐标原点),当直线1的倾斜角 为锐角时,求
为锐角时,求 的取值范围.
的取值范围.
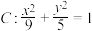 长轴的左,右顶点分别为A,B.
长轴的左,右顶点分别为A,B.(1)若P、Q是椭圆上关于x轴对称的两点,直线
 的斜率分别为
的斜率分别为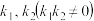 ,求
,求 的最小值;
的最小值;(2)已知过点
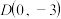 的直线l交椭圆C于M、N两个不同的点,直线
的直线l交椭圆C于M、N两个不同的点,直线 分别交y轴于点S、T,记
分别交y轴于点S、T,记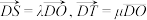 (O为坐标原点),当直线1的倾斜角
(O为坐标原点),当直线1的倾斜角 为锐角时,求
为锐角时,求 的取值范围.
的取值范围.
您最近半年使用:0次
2021-09-05更新
|
809次组卷
|
6卷引用:专题3.3 圆锥曲线与方程 章末检测3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)
(已下线)专题3.3 圆锥曲线与方程 章末检测3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)湖南省长沙市长郡中学2021-2022学年高三上学期第一次月考数学试题(已下线)专题6.3 期中押题检测卷(考试范围:第1-3章)3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册) (已下线)专题7.3 期末押题检测卷(考试范围:选择性必修第一册)3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)河北省唐山市开滦第二中学2023届高三考前保温数学试题山西省运城市景胜学校2023-2024学年高二上学期11月月考数学试题A卷
20-21高二下·重庆渝中·期末
名校
解题方法
4 . 阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点 与两定点
与两定点 ,
, 的距离之比
的距离之比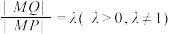 ,
, 是一个常数,那么动点
是一个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为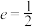 .
.
(1)求椭圆 的标准方程;
的标准方程;
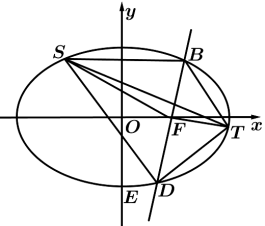
(2)如图,过右焦点 斜率为
斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, (点
(点 在
在 轴上方),点
轴上方),点 ,
, 是椭圆
是椭圆 上异于
上异于 ,
, 的两点,
的两点,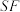 平分
平分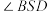 ,
,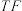 平分
平分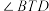 .
.
①求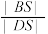 的取值范围;
的取值范围;
②将点 、
、 、
、 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的面积为
外接圆的面积为 ,求直线
,求直线 的方程.
的方程.
 与两定点
与两定点 ,
, 的距离之比
的距离之比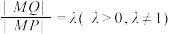 ,
, 是一个常数,那么动点
是一个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为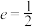 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)如图,过右焦点
 斜率为
斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, (点
(点 在
在 轴上方),点
轴上方),点 ,
, 是椭圆
是椭圆 上异于
上异于 ,
, 的两点,
的两点,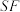 平分
平分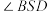 ,
,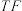 平分
平分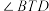 .
.①求
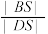 的取值范围;
的取值范围;②将点
 、
、 、
、 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的面积为
外接圆的面积为 ,求直线
,求直线 的方程.
的方程.
您最近半年使用:0次
2021-07-12更新
|
4943次组卷
|
10卷引用:第3章 圆锥曲线与方程 单元综合检测(能力提升)(单元培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)
(已下线)第3章 圆锥曲线与方程 单元综合检测(能力提升)(单元培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)(已下线)专题08 《圆锥曲线与方程》中的解答题压轴题(2)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 重庆市巴蜀中学2020-2021学年高二下学期期末数学试题(已下线)专题12 圆锥曲线的方程的压轴题(二)-【尖子生专用】2021-2022学年高二数学考点培优训练(人教A版2019选择性必修第一册)(已下线)专题1 阿波罗尼斯圆及其应用 微点4 阿波罗尼斯圆与圆锥曲线重庆市南开中学校2023届高三上学期期末数学试题安徽省合肥一六八中学等学校2024届高三上学期名校期末联合测试数学试题安徽“耀正优+”2024届高三名校上学期期末测试数学试题(已下线)圆锥曲线新定义(已下线)信息必刷卷01(江苏专用,2024新题型)



