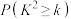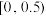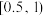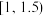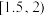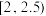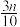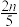真题
解题方法
1 . 某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
(1)填写如下列联表:
能否有 的把握认为甲、乙两车间产品的优级品率存在差异?能否有
的把握认为甲、乙两车间产品的优级品率存在差异?能否有 的把握认为甲,乙两车间产品的优级品率存在差异?
的把握认为甲,乙两车间产品的优级品率存在差异?
(2)已知升级改造前该工厂产品的优级品率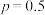 ,设
,设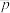 为升级改造后抽取的n件产品的优级品率.如果
为升级改造后抽取的n件产品的优级品率.如果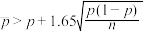 ,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(
,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(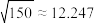 )
)
附:
优级品 | 合格品 | 不合格品 | 总计 | |
甲车间 | 26 | 24 | 0 | 50 |
乙车间 | 70 | 28 | 2 | 100 |
总计 | 96 | 52 | 2 | 150 |
(1)填写如下列联表:
优级品 | 非优级品 | |
甲车间 | ||
乙车间 |
 的把握认为甲、乙两车间产品的优级品率存在差异?能否有
的把握认为甲、乙两车间产品的优级品率存在差异?能否有 的把握认为甲,乙两车间产品的优级品率存在差异?
的把握认为甲,乙两车间产品的优级品率存在差异?(2)已知升级改造前该工厂产品的优级品率
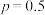 ,设
,设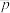 为升级改造后抽取的n件产品的优级品率.如果
为升级改造后抽取的n件产品的优级品率.如果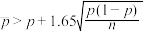 ,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(
,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(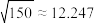 )
)附:

| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
昨日更新
|
3638次组卷
|
7卷引用:专题09统计与成对数据的统计分析
专题09统计与成对数据的统计分析专题33概率统计解答题(第二部分)(已下线)2024年高考数学真题完全解读(全国甲卷理科)(已下线)2024年高考全国甲卷数学(文)真题变式题16-23(已下线)2024年高考全国甲卷数学(理)真题变式题16-232024年高考全国甲卷数学(理)真题2024年高考全国甲卷数学(文)真题
2024高三·上海·专题练习
2 . 为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29000名学生中抽取580人,得到日均体育锻炼时长与学业成绩的数据如下表所示:
(1)该地区29000名学生中体育锻炼时长不少于1小时的人数约为多少?
(2)估计该地区初中学生日均体育锻炼的时长(精确到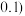 .
.
(3)是否有 的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
时间范围 |
|
|
|
|
|
学业成绩 | |||||
优秀 | 5 | 44 | 42 | 3 | 1 |
不优秀 | 134 | 147 | 137 | 40 | 27 |
(2)估计该地区初中学生日均体育锻炼的时长(精确到
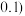 .
.(3)是否有
 的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
您最近一年使用:0次
3 . 学生的安全是关乎千家万户的大事,对学生进行安全教育是学校教育的一个重要方面.临近暑假,某市教体局针对当前的实际情况,组织各学校进行安全教育,并进行了安全知识和意识的测试,满分100分,成绩不低于60分为合格,否则为不合格.为了解安全教育的成效,随机抽查了辖区内某校180名学生的测试成绩,将统计结果制作成如图所示的频率分布直方图.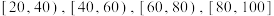 内的女生人数分别为
内的女生人数分别为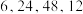 ,完成
,完成 列联表,根据小概率值
列联表,根据小概率值 的独立性检验,能否认为测试成绩与性别有关联?
的独立性检验,能否认为测试成绩与性别有关联?
(2)若对抽查学生的测试成绩进行量化转换,“合格”记5分,“不合格”记0分.按比例分配的分层随机抽样的方法从“合格”与“不合格”的学生中随机选取10人进行座谈,再从这10人中任选4人,记所选4人的量化总分为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附: ,其中
,其中 .
.

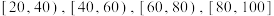 内的女生人数分别为
内的女生人数分别为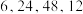 ,完成
,完成 列联表,根据小概率值
列联表,根据小概率值 的独立性检验,能否认为测试成绩与性别有关联?
的独立性检验,能否认为测试成绩与性别有关联?| 不合格 | 合格 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 ,其中
,其中 .
. | 0.1 | 0.05 | 0.005 |
 | 2.706 | 3.841 | 7.879 |
您最近一年使用:0次
7日内更新
|
286次组卷
|
3卷引用:统计与成对数据的统计分析-综合测试卷B卷
名校
4 . 某工厂生产某款电池,在满电状态下能够持续放电时间不低于10小时的为合格品,工程师选择某台生产电池的机器进行参数调试,在调试前后,分别在其产品中随机抽取样本数据进行统计,制作了如下的频率分布直方图和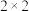 列联表:
列联表:
(1)求列联表中a,b的值;
(2)补充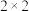 列联表,能否有95%的把握认为参数调试与产品质量有关;
列联表,能否有95%的把握认为参数调试与产品质量有关;
(3)常用 表示在事件A发生的条件下事件B发生的优势,在统计中称为似然比.现从调试前、后的产品中任取一件,A表示“选到的产品是不合格品”,B表示“选到的产品是调试后的产品”,请利用样本数据,估计
表示在事件A发生的条件下事件B发生的优势,在统计中称为似然比.现从调试前、后的产品中任取一件,A表示“选到的产品是不合格品”,B表示“选到的产品是调试后的产品”,请利用样本数据,估计 的值.
的值.
附: ,
, .
.
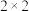 列联表:
列联表: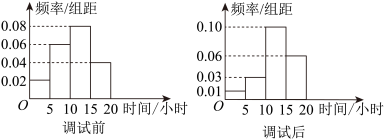
| 产品 | 合格 | 不合格 | 合计 |
| 调试前 | a | 16 | |
| 调试后 | b | 12 | |
| 合计 |
(1)求列联表中a,b的值;
(2)补充
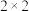 列联表,能否有95%的把握认为参数调试与产品质量有关;
列联表,能否有95%的把握认为参数调试与产品质量有关;(3)常用
 表示在事件A发生的条件下事件B发生的优势,在统计中称为似然比.现从调试前、后的产品中任取一件,A表示“选到的产品是不合格品”,B表示“选到的产品是调试后的产品”,请利用样本数据,估计
表示在事件A发生的条件下事件B发生的优势,在统计中称为似然比.现从调试前、后的产品中任取一件,A表示“选到的产品是不合格品”,B表示“选到的产品是调试后的产品”,请利用样本数据,估计 的值.
的值.附:
 ,
, .
. | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
名校
解题方法
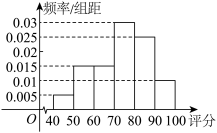
5 . 某校为了给高三学生举办“18岁成人礼”活动,由团委草拟了活动方案,并以问卷的形式调查了部分同学对活动方案的评分(满分100分),所得评分统计如图所示. 的人数为
的人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.
(2)为了解评分是否与性别有关,随机抽取了部分问卷,统计结果如下表所示,则依据 的独立性检验,能否认为评分与性别有关?
的独立性检验,能否认为评分与性别有关?
(3)若将(2)中表格的人数数据都扩大为原来的10倍,则依据 的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
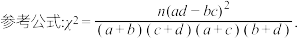
参考数据:
 的人数为
的人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.(2)为了解评分是否与性别有关,随机抽取了部分问卷,统计结果如下表所示,则依据
 的独立性检验,能否认为评分与性别有关?
的独立性检验,能否认为评分与性别有关?| 男生 | 女生 | |
评分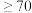 | 30 | 35 |
评分 | 20 | 15 |
(3)若将(2)中表格的人数数据都扩大为原来的10倍,则依据
 的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.
的独立性检验,所得结论与(2)中所得结论是否一致?直接给出结论即可,不必书写计算过程.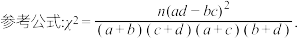
参考数据:
 | 0.1 | 0.05 | 0.01 |
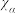 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
名校
6 . 贵州省“美丽乡村”篮球联赛在比赛间隙进行芦笙舞、侗族大歌等非物质文化遗产展演,这项活动将体育运动与当地民族民俗文化相触合,创造出独特的文体公共产品.为了打造更具吸引力的赛事,某平台发起了群众观赛意见反馈调查,共收回了200份调查问卷.
(1)通过进一步分析关注赛事群众的调查问卷得知,关注表演的女性用户有24名,现从关注赛事的群众中抽取一人,设“抽取的一人为男性”为事件A,“抽取的一人关注表演”为事件B,若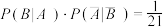 ,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
(2)是否有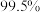 的把握认为是否关注赛事与性别有关?
的把握认为是否关注赛事与性别有关?
附: ,其中
,其中 .
.
性别 | 关注赛事 | 不关注赛事 |
男 | 84 | 36 |
女 | 40 | 40 |
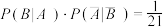 ,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;
,则以此次调查的数据为依据,估计从平台用户中任意抽取一名用户,该用户关注表演的概率为多少;(2)是否有
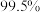 的把握认为是否关注赛事与性别有关?
的把握认为是否关注赛事与性别有关?附:
 ,其中
,其中 .
.
| 0.050 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
7 . 2023年12月30日8时13分,长征二号丙/远征一号S运载火箭在酒泉卫星发射中心点火起飞,随后成功将卫星互联网技术试验卫星送入预定轨道.由中国航天科技集团有限公司研制的运载火箭48次宇航任务全部取得圆满成功.也代表着中国航天2023年完美收官.某市一调研机构为了了解当地学生对我国航天事业发展的关注度,随机从本市大学生和高中生中抽取一个容量为 的样本,根据调查结果得到如下列联表:
的样本,根据调查结果得到如下列联表:
(1)完成上述列联表;依据小概率值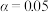 的独立性检验,认为关注航天事业发展与学生群体有关联,求样本容量n的最小值;
的独立性检验,认为关注航天事业发展与学生群体有关联,求样本容量n的最小值;
(2)用频率估计概率,从本市大学生和高中生中随机选取3人,用X表示不关注的人数,求X的分布列和数学期望.
附:
 ,其中
,其中 .
.
 的样本,根据调查结果得到如下列联表:
的样本,根据调查结果得到如下列联表:学生群体 | 关注度 | 合计 | |
关注 | 不关注 | ||
大学生 |
|
| |
高中生 | |||
合计 |
| ||
(1)完成上述列联表;依据小概率值
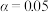 的独立性检验,认为关注航天事业发展与学生群体有关联,求样本容量n的最小值;
的独立性检验,认为关注航天事业发展与学生群体有关联,求样本容量n的最小值;(2)用频率估计概率,从本市大学生和高中生中随机选取3人,用X表示不关注的人数,求X的分布列和数学期望.
附:
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.
您最近一年使用:0次
解题方法
8 . 某公司新研发了一款智能灯,此灯有拍照搜题功能,学生遇到疑难问题,通过拍照搜题后,会在显示屏上显示该题的解答过程以及该题考查的知识点与相应的解题方法该产品投入市场三个月后,公司对部分用户做了调研:抽取了200位使用者,每人填写一份评分表(满分为100分),现从200份评分表中,随机抽取40份(其中男、女使用者的评分表各20份)
作为样本,经统计得到如下的数据:
女生使用者评分:67,71,72,75,80,83,83,83,84,84,85,86,88,90,90,91,92,92,92,92
男生使用者评分:67,68,69,69,70,72,72,73,74,75,76,76,77,78,79,82,84,84,89,92
记该样本的中位数为 ,按评分情况将使用.都对该智能灯的态度分为两种类型:评分不小于
,按评分情况将使用.都对该智能灯的态度分为两种类型:评分不小于 的称为“满意型”,其余的都称为“不满意型”.
的称为“满意型”,其余的都称为“不满意型”.
(1)求 的值,填写如下
的值,填写如下 列联表
列联表
(2)能否有 的把握认为满意与性别有关?
的把握认为满意与性别有关?
参考公式与数据:
作为样本,经统计得到如下的数据:
女生使用者评分:67,71,72,75,80,83,83,83,84,84,85,86,88,90,90,91,92,92,92,92
男生使用者评分:67,68,69,69,70,72,72,73,74,75,76,76,77,78,79,82,84,84,89,92
记该样本的中位数为
 ,按评分情况将使用.都对该智能灯的态度分为两种类型:评分不小于
,按评分情况将使用.都对该智能灯的态度分为两种类型:评分不小于 的称为“满意型”,其余的都称为“不满意型”.
的称为“满意型”,其余的都称为“不满意型”.(1)求
 的值,填写如下
的值,填写如下 列联表
列联表女生评分 | 男生评分 | 合计 | |
“满意型”人数 | |||
“不满意型”人数 | |||
合计 |
 的把握认为满意与性别有关?
的把握认为满意与性别有关?参考公式与数据:

| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
您最近一年使用:0次
解题方法
9 . 绿化祖国要扩绿、兴绿、护绿并举.某校植树节分别在甲,乙两块不同的土地上栽种某品种树苗各500株.甲地土质含有 元素,乙地土质不含有
元素,乙地土质不含有 元素,其它土质情况均相同,一段时间后,为了弄清楚该品种树苗的成活情况与
元素,其它土质情况均相同,一段时间后,为了弄清楚该品种树苗的成活情况与 元素含量是否有关联,分别在甲,乙两块土地上随机抽取树苗各50株作为样本进行统计分析.经统计,甲地成活45株,乙地成活40株.
元素含量是否有关联,分别在甲,乙两块土地上随机抽取树苗各50株作为样本进行统计分析.经统计,甲地成活45株,乙地成活40株.
(1)根据所给数据,完成下面的 列联表(单位:株),并判断依据小概率值
列联表(单位:株),并判断依据小概率值 的独立性检验,能否认为该品种树苗成活与
的独立性检验,能否认为该品种树苗成活与 元素含量有关联?
元素含量有关联?
 列联表
列联表
(2)从样本中不成活的树苗中随机抽取3株,其中取自甲地的株数为 ,求
,求 的分布列及方差
的分布列及方差
参考公式: ,
,
参考数据:
 元素,乙地土质不含有
元素,乙地土质不含有 元素,其它土质情况均相同,一段时间后,为了弄清楚该品种树苗的成活情况与
元素,其它土质情况均相同,一段时间后,为了弄清楚该品种树苗的成活情况与 元素含量是否有关联,分别在甲,乙两块土地上随机抽取树苗各50株作为样本进行统计分析.经统计,甲地成活45株,乙地成活40株.
元素含量是否有关联,分别在甲,乙两块土地上随机抽取树苗各50株作为样本进行统计分析.经统计,甲地成活45株,乙地成活40株.(1)根据所给数据,完成下面的
 列联表(单位:株),并判断依据小概率值
列联表(单位:株),并判断依据小概率值 的独立性检验,能否认为该品种树苗成活与
的独立性检验,能否认为该品种树苗成活与 元素含量有关联?
元素含量有关联? 列联表
列联表| 类别 | 树苗成活情况 | 合计 | |
| 成活 | 不成活 | ||
含 元素 元素 | |||
不含 元素 元素 | |||
| 合计 | |||
(2)从样本中不成活的树苗中随机抽取3株,其中取自甲地的株数为
 ,求
,求 的分布列及方差
的分布列及方差参考公式:
 ,
,
参考数据:
 | 0.10 | 0.05 | 0.010 | 0.005 |
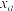 | 2.706 | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次
10 . 为促进全面阅读,建设书香校园,鼓励学生参加阅读活动,某校随机抽查了男、女生各200名,统计他们在暑假期间每天阅读时长,并把每天阅读时长超过1小时的记为“阅读达标”,时长不超过1小时的记为“阅读不达标”,阅读达标与阅读不达标的人数比为 ,阅读达标的女生与男生的人数比为
,阅读达标的女生与男生的人数比为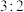 .
.
(1)完成下面的 列联表:
列联表:
(2)根据上述数据,依据小概率值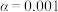 的独立性检验,能否认为“阅读达标情况”与“性别”有关联?
的独立性检验,能否认为“阅读达标情况”与“性别”有关联?
(3)从阅读达标的学生中按男、女生人数比例用分层随机抽样的方法抽取5人进行座谈,再从这5人中任选2人,记这2人中男生人数为X,求X的分布列和数学期望.
参考公式: ,
, .
.
 ,阅读达标的女生与男生的人数比为
,阅读达标的女生与男生的人数比为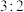 .
.(1)完成下面的
 列联表:
列联表:性别 | 阅读达标情况 | 合计 | |
阅读达标 | 阅读不达标 | ||
男生 | |||
女生 | |||
合计 | |||
(2)根据上述数据,依据小概率值
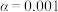 的独立性检验,能否认为“阅读达标情况”与“性别”有关联?
的独立性检验,能否认为“阅读达标情况”与“性别”有关联?(3)从阅读达标的学生中按男、女生人数比例用分层随机抽样的方法抽取5人进行座谈,再从这5人中任选2人,记这2人中男生人数为X,求X的分布列和数学期望.
参考公式:
 ,
, .
.
| 0.10 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2024-05-12更新
|
648次组卷
|
4卷引用:专题4 考前押题大猜想16-20
(已下线)专题4 考前押题大猜想16-20甘肃省酒泉市2024届高三第三次诊断考试(5月)数学试题四川省内江市第三中学2024届高三第一次适应性考试数学(理科)试卷(已下线)专题06 统计模型的热点题型(7类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)