名校
1 . 新能源汽车是指除汽油、柴油发动机之外的所有其他能源汽车,被认为能减少空气污染和缓解能源短缺的压力.在当今提倡全球环保的前提下,新能源汽车越来越受到消费者的青睐,新能源汽车产业也必将成为未来汽车产业发展的导向与目标.某车企调查了近期购车的200位车主的性别与购车种类的情况,得到如下数据:
(1)根据表中数据,判断能否有95%的把握认为是否购置新能源汽车与性别有关;
(2)已知该车企有5种款式不同的汽车,每种款式的汽车均有新能源和传统燃油两种类型各1辆.假设某单位从这10辆汽车中随机购买4辆汽车,设其中款式相同的汽车的对数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
附: ,
, .
.
| 购置新能源汽车 | 购置传统燃油汽车 | 总计 | |
| 男性 | 80 | 20 | 100 |
| 女性 | 65 | 35 | 100 |
| 总计 | 145 | 55 | 200 |
(2)已知该车企有5种款式不同的汽车,每种款式的汽车均有新能源和传统燃油两种类型各1辆.假设某单位从这10辆汽车中随机购买4辆汽车,设其中款式相同的汽车的对数为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.附:
 ,
, .
. | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.706 | 3.841 | 5.024 | 6.635 |
您最近一年使用:0次
2022-03-26更新
|
971次组卷
|
3卷引用:福建省福州第一中学2022届高三质检三模数学试题
名校
2 . 为了解某工业园中员工的颈椎疾病与工作性质是否有关,在工业园内随机的对其中50名工作人员是否患有颈椎疾病进行了抽样调查,得到如下的列联表.
已知在全部50人中随机抽取1人,抽到患有颈椎疾病的人的概率为 .
.
(1)①请完成上表;
②依据小概率值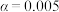 的独立性检验,分析患颈椎疾病与工作性质有关?
的独立性检验,分析患颈椎疾病与工作性质有关?
(2)已知在患有颈椎疾病的10名蓝领中,有3人工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中 ,
,
| 患有颈椎疾病 | 没有患颈椎疾病 | 合计 | |
| 白领 | 5 | ||
| 蓝领 | 10 | ||
| 合计 | 50 |
 .
.(1)①请完成上表;
②依据小概率值
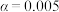 的独立性检验,分析患颈椎疾病与工作性质有关?
的独立性检验,分析患颈椎疾病与工作性质有关?(2)已知在患有颈椎疾病的10名蓝领中,有3人工龄在15年以上,现在从患有颈椎疾病的10名蓝领中,选出3人进行工龄的调查,记选出工龄在15年以上的人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.附:
 ,其中
,其中 ,
, | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2023-05-11更新
|
421次组卷
|
2卷引用:福建省南平市高级中学2022-2023学年高二下学期期中考试数学试题
解题方法
3 . 针对时下的“抖音热”,校团委对“学生性别和喜欢抖音是否有关”作了调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的 ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数 ,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
附表:
附:
 ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数 ,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人附表:
 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |

| A.20 | B.30 | C.35 | D.40 |
您最近一年使用:0次
2023-12-21更新
|
514次组卷
|
3卷引用:福建省漳州市东山第二中学2021-2022学年高二下学期期中考试数学(A)试题
解题方法
4 . 武汉热干面既是中国四大名面之一,也是湖北武汉最出名的小吃之一.某热干面店铺连续10天的销售情况如下(单位:份):
(1)分别求套餐一、套餐二的均值、方差,并判断两种套餐销售的稳定情况;
(2)假定在连续10天中每位顾客只购买了一份,根据图表内容填写下列 列联表,并据此判断能否有95%的把握认定顾客性别与套餐选择有关?
列联表,并据此判断能否有95%的把握认定顾客性别与套餐选择有关?
附: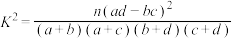
| 天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 套餐一 | 120 | 100 | 140 | 140 | 120 | 70 | 150 | 120 | 110 | 130 |
| 套餐二 | 80 | 90 | 90 | 60 | 50 | 90 | 70 | 80 | 90 | 100 |
(2)假定在连续10天中每位顾客只购买了一份,根据图表内容填写下列
 列联表,并据此判断能否有95%的把握认定顾客性别与套餐选择有关?
列联表,并据此判断能否有95%的把握认定顾客性别与套餐选择有关?| 顾客套餐 | 套餐一 | 套餐二 | 合计 |
| 男顾客 | 400 | ||
| 女顾客 | 500 | ||
| 合计 |
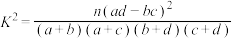
 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.706 | 3.841 | 5.024 | 6.635 |
您最近一年使用:0次
2022-01-26更新
|
871次组卷
|
4卷引用:福建省漳州市东山第二中学2022-2023学年高二下学期期中数学试题
名校
解题方法
5 . 民族要复兴,乡村要振兴,合作社助力乡村产业振兴,农民专业合作社已成为新型农业经营主体和现代农业建设的中坚力量,为实施乡村振兴战略作出了巨大的贡献.已知某主要从事手工编织品的农民专业合作社共有100名编织工人,该农民专业合作社为了鼓励工人,决定对“编织巧手”进行奖励,为研究“编织巧手”是否与年龄有关,现从所有编织工人中抽取40周岁以上(含40周岁)的工人24名,40周岁以下的工人16名,得到的数据如表所示.
(1)请完成答题卡上的 列联表,并判断能否有
列联表,并判断能否有 的把握认为是否是“编织巧手”与年龄有关;
的把握认为是否是“编织巧手”与年龄有关;
(2)为进一步提高编织效率,培养更多的“编织巧手”,该农民专业合作社决定从上表中的非“编织巧手”的工人中采用分层抽样的方法抽取6人参加技能培训,再从这6人中随机抽取2人分享心得,求这2人中恰有1人的年龄在40周岁以下的概率.
参考公式: ,其中
,其中 .
.
参考数据:
“编织巧手” | 非“编织巧手” | 总计 | |
年龄 | 19 | ||
年龄 | 10 | ||
总计 | 40 |
 列联表,并判断能否有
列联表,并判断能否有 的把握认为是否是“编织巧手”与年龄有关;
的把握认为是否是“编织巧手”与年龄有关;(2)为进一步提高编织效率,培养更多的“编织巧手”,该农民专业合作社决定从上表中的非“编织巧手”的工人中采用分层抽样的方法抽取6人参加技能培训,再从这6人中随机抽取2人分享心得,求这2人中恰有1人的年龄在40周岁以下的概率.
参考公式:
 ,其中
,其中 .
.参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2023-05-20更新
|
548次组卷
|
14卷引用:福建省厦门第一中学2022-2023学年高二下学期6月月考数学试题
福建省厦门第一中学2022-2023学年高二下学期6月月考数学试题湖南省部分学校2023届高三下学期5月联数学试题河南省驻马店市2023届高三二模理科数学试题四川省南江中学2023届高三下学期五月适应性考试(一)理科数学试题四川省南江中学2023届高三下学期五月适应性考试(一)文科数学试题吉林省长春市十一高中2022-2023学年高二下学期第二学程考试数学试题云南省保山市文山州2022-2023学年高二下学期期末考试数学试题(已下线)高二下学期期末押题卷02-【同步题型讲义】2022-2023学年高二数学同步教学题型讲义(人教A版2019选择性必修)贵州省2023届高三多校联考数学(文)试题辽宁省大连市第八中学2022-2023学年高二下学期6月月考数学试题河南省创新发展联盟2023届高三仿真模拟预测理科数学试题河南省驻马店市2023届高三第二次联考文科数学试题河南省创新发展联盟2023届高三高考仿真模拟预测文科数学试题四川省绵阳市三台中学校2024届高三下学期第一次仿真测试理科数学试题
名校
6 . 某学校研究性学习小组对该校高二学生视力情况进行调查,在高二的全体 名学生中随机抽取了
名学生中随机抽取了 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在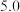 以下的人数;
以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在 名和
名和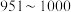 名的学生进行了调查,得到右表中数据,根据
名的学生进行了调查,得到右表中数据,根据 分布概率表中的数据,能否有
分布概率表中的数据,能否有 的把握认为视力与学习成绩有关系?请说明理由;
的把握认为视力与学习成绩有关系?请说明理由;
(3)在(2)中调查的 名学生中,按照分层抽样在不近视的学生中抽取了
名学生中,按照分层抽样在不近视的学生中抽取了 人进一步调查他们良好的护眼习惯,并且在这
人进一步调查他们良好的护眼习惯,并且在这 人中任取
人中任取 人,记名次在
人,记名次在 的学生人数为
的学生人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附:
 .其中
.其中 .
.
 名学生中随机抽取了
名学生中随机抽取了 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
| 年级名次 是否近视 |  | 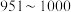 |
| 近视 |  |  |
| 不近视 |  |  |
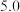 以下的人数;
以下的人数;(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在
 名和
名和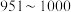 名的学生进行了调查,得到右表中数据,根据
名的学生进行了调查,得到右表中数据,根据 分布概率表中的数据,能否有
分布概率表中的数据,能否有 的把握认为视力与学习成绩有关系?请说明理由;
的把握认为视力与学习成绩有关系?请说明理由;(3)在(2)中调查的
 名学生中,按照分层抽样在不近视的学生中抽取了
名学生中,按照分层抽样在不近视的学生中抽取了 人进一步调查他们良好的护眼习惯,并且在这
人进一步调查他们良好的护眼习惯,并且在这 人中任取
人中任取 人,记名次在
人,记名次在 的学生人数为
的学生人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
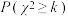 |  | 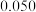 |  |  |  |
 |  |  |  |  |  |
 .其中
.其中 .
.
您最近一年使用:0次
2023-07-05更新
|
327次组卷
|
17卷引用:2015-2016学年福建省上杭县一中高二下周练文科数学试卷
2015-2016学年福建省上杭县一中高二下周练文科数学试卷2015届吉林省吉林市高三第三次模拟考试理科数学试卷2016届河北省正定中学高三上第五次月考理科数学试卷2015-2016学年湖北武汉华中师大一附高二上期末理数学卷2016届湖北武汉华中师大一附高三5月月考理科数学试卷2017届内蒙古杭锦后旗奋斗中学高三上入学摸底数学理试卷2016届陕西黄陵中学高三下二模考试数学(理)试卷陕西省西安市长安区第一中学2017届高三4月模拟考试数学(理)试题【全国百强校】宁夏吴忠中学2017-2018学年高二下学期期中考试数学(理)试题【全国百强校】甘肃省西北师范大学附属中学2018届高三冲刺诊断考试数学(理)试题【全国百强校】吉林省实验中学2019届高三下学期第八次月考数学(理)试题重庆市第一中学2019-2020学年高三下学期3月月考数学(理)试题甘肃省兰州市外国语高级中学2022届高三上学期9月建标考试理科数学试题上海市闵行(文绮)中学2023届高三下学期开学学情调研数学试题上海市奉贤区2022-2023学年高二下学期期末数学试题(已下线)8.3 2?2列联表(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)(已下线)专题07概率初步(续)--高二期末考点大串讲(沪教版2020选修)
名校
解题方法
7 . 某学校为了了解高中生的航空航天知识情况,设计了一份调查问卷,从该学校高中生中随机抽选200名学生进行调查,调查样本中男生、女生各100名,下图是根据样本调查结果绘制的等高堆积条形图.
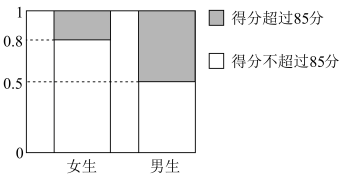
(1)请将上面列联表填写完整.
(2)依据 的独立性检验,能否认为该学校高中生了解航空航天知识程度与性别有关联?
的独立性检验,能否认为该学校高中生了解航空航天知识程度与性别有关联?
(3)现从得分超过85分的同学中采用按性别比例分配的分层抽样方法抽取7人,再从这7人中随机抽选3人参加下一轮调查,记 为选出参加下一轮调查的女生的人数,求随机变量
为选出参加下一轮调查的女生的人数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
附:参考公式: ,其中
,其中
下表是 独立性检验中几个常用的小概率值和相应的临界值
独立性检验中几个常用的小概率值和相应的临界值

性别 | 了解航空航天知识程度 | 合计 | |
得分不超过85分的人数 | 得分超过85分的人数 | ||
女生 | |||
男生 | |||
合计 | |||
(2)依据
 的独立性检验,能否认为该学校高中生了解航空航天知识程度与性别有关联?
的独立性检验,能否认为该学校高中生了解航空航天知识程度与性别有关联?(3)现从得分超过85分的同学中采用按性别比例分配的分层抽样方法抽取7人,再从这7人中随机抽选3人参加下一轮调查,记
 为选出参加下一轮调查的女生的人数,求随机变量
为选出参加下一轮调查的女生的人数,求随机变量 的分布列和数学期望.
的分布列和数学期望.附:参考公式:
 ,其中
,其中
下表是
 独立性检验中几个常用的小概率值和相应的临界值
独立性检验中几个常用的小概率值和相应的临界值
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2022-05-10更新
|
773次组卷
|
4卷引用:福建省德化第一中学2021-2022学年高二下学期第二次质检数学试题
8 . 某校筹办运动会,设计了方案一、方案二两种方案、为了解对这两种方案的支持情况,在校内随机抽取 名同学,得到数据如下:
名同学,得到数据如下:
假设校内所有同学支持何种方案互不影响.
(1)依据所给数据及小概率值 的独立性检验,能否认为支持方案一与性别有关?
的独立性检验,能否认为支持方案一与性别有关?
(2)以抽取的 名同学的支持率高低为决策依据,应选择哪种方案?
名同学的支持率高低为决策依据,应选择哪种方案?
(3)用频率估计概率,从全校支持方案一的学生中随机抽取 人,其中男生的人数记为
人,其中男生的人数记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
附: ,其中
,其中 .
.
 名同学,得到数据如下:
名同学,得到数据如下: | 男 | 女 | |||
| 支持 | 不支持 | 支持 | 不支持 | |
| 方案一 |  人 人 |  人 人 |  人 人 |  人 人 |
| 方案二 | 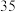 人 人 | 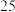 人 人 | 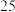 人 人 |  人 人 |
(1)依据所给数据及小概率值
 的独立性检验,能否认为支持方案一与性别有关?
的独立性检验,能否认为支持方案一与性别有关?(2)以抽取的
 名同学的支持率高低为决策依据,应选择哪种方案?
名同学的支持率高低为决策依据,应选择哪种方案?(3)用频率估计概率,从全校支持方案一的学生中随机抽取
 人,其中男生的人数记为
人,其中男生的人数记为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.附:
 ,其中
,其中 .
.  |  |  |  |  |  |
 |  |  |  |  |  |
您最近一年使用:0次
名校
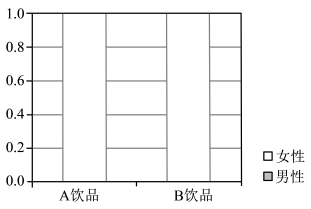
9 . 厦门思明区沙坡尾某网红店推出A、B两种不同风味的饮品.为了研究消费者性别和饮品偏好的关联性,店主调查了首次到店的消费者,整理得到如下列联表:
表1单位:人
(1)请画出列联表的等高堆积条形图,并依据小概率值 的独立性检验,判断首次到店消费者的性别与饮品风味偏好是否有关联.如果结论是性别与饮品风味偏好有关联,请解释它们之间如何相互影响.
的独立性检验,判断首次到店消费者的性别与饮品风味偏好是否有关联.如果结论是性别与饮品风味偏好有关联,请解释它们之间如何相互影响.
(2)店主进一步调查发现:女性消费者若前一次选择A饮品,则下一次选择A、B两种饮品的概率分别为 、
、 ;若前一次选择B饮品,则下一次选择A、B两种饮品的概率分别为
;若前一次选择B饮品,则下一次选择A、B两种饮品的概率分别为 、
、 ;如此循环下去,求女性消费者前三次选择A、B两种饮品的数学期望,并解释其实际含义.
;如此循环下去,求女性消费者前三次选择A、B两种饮品的数学期望,并解释其实际含义.
附: .
.
表1单位:人
性别 | 种类 | 合计 | |
A饮品 | B饮品 | ||
女性 | 60 | 40 | 100 |
男性 | 40 | 60 | 100 |
合计 | 100 | 100 | 200 |
 的独立性检验,判断首次到店消费者的性别与饮品风味偏好是否有关联.如果结论是性别与饮品风味偏好有关联,请解释它们之间如何相互影响.
的独立性检验,判断首次到店消费者的性别与饮品风味偏好是否有关联.如果结论是性别与饮品风味偏好有关联,请解释它们之间如何相互影响.
(2)店主进一步调查发现:女性消费者若前一次选择A饮品,则下一次选择A、B两种饮品的概率分别为
 、
、 ;若前一次选择B饮品,则下一次选择A、B两种饮品的概率分别为
;若前一次选择B饮品,则下一次选择A、B两种饮品的概率分别为 、
、 ;如此循环下去,求女性消费者前三次选择A、B两种饮品的数学期望,并解释其实际含义.
;如此循环下去,求女性消费者前三次选择A、B两种饮品的数学期望,并解释其实际含义.附:
 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
名校
10 . 近年来,师范专业是高考考生填报志愿的热门专业.某高中随机调查了本校2022年参加高考的90位文科考生首选志愿(第一个院校专业组的第一个专业)填报情况,经统计,首选志愿填报与性别情况如下表:(单位:人)
(1)根据表中数据.能否有95%的把握认为首选志愿为师范专业与性别有关?
(2)用样本估计总体,用本次调研中首选志愿样本的频率代替首选志愿的概率,从2022年全国文科考生中随机抽取3人,设被抽取的3人中首选志愿为师范专业的人数为 ,求
,求 的分布列、数学期望
的分布列、数学期望 和方差
和方差 .
.
附: ,
, .
.
首选志愿为师范专业 | 首选志愿为非师范专业 | |
女性 | 25 | 35 |
男性 | 5 | 25 |
(2)用样本估计总体,用本次调研中首选志愿样本的频率代替首选志愿的概率,从2022年全国文科考生中随机抽取3人,设被抽取的3人中首选志愿为师范专业的人数为
 ,求
,求 的分布列、数学期望
的分布列、数学期望 和方差
和方差 .
.附:
 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2022-09-03更新
|
689次组卷
|
6卷引用:福建省连城县第一中学2023届高三上学期第一次月考数学试题

 40岁
40岁 40岁
40岁