1 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记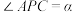 ,
,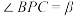 ,
, ,二面角
,二面角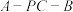 的大小为
的大小为 ,则
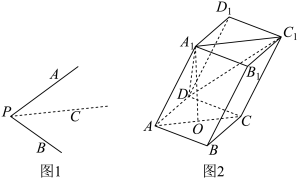
,则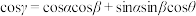 .如图2,四棱柱
.如图2,四棱柱 中,
中,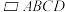 为菱形,
为菱形, ,
,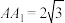 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.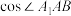 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: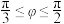 ;
;
(3)过点 作平面
作平面 ,使平面
,使平面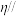 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记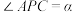 ,
,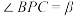 ,
, ,二面角
,二面角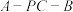 的大小为
的大小为 ,则
,则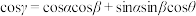 .如图2,四棱柱
.如图2,四棱柱 中,
中,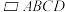 为菱形,
为菱形, ,
,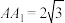 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
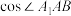 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: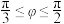 ;
;(3)过点
 作平面
作平面 ,使平面
,使平面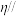 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
您最近一年使用:0次
2024-07-20更新
|
811次组卷
|
6卷引用:山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题
山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2(已下线)拔高点突破04 新情景、新定义下的立体几何问题(六大题型)-1河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题山东省德州市夏津育中万隆中英文高级中学2024-2025学年高二上学期第一次月考数学试题
名校
解题方法
2 . 人脸识别是基于人的脸部特征进行身份识别的一种生物识别技术.主要应用距离测试样本之间的相似度,常用测量距离的方式有3种.设 ,
, ,则欧几里得距离
,则欧几里得距离 ;曼哈顿距离
;曼哈顿距离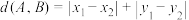 ,余弦距离
,余弦距离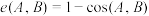 ,其中
,其中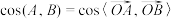 (
( 为坐标原点).
为坐标原点).
(1)若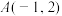 ,
,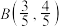 ,求
,求 ,
, 之间的曼哈顿距离
之间的曼哈顿距离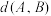 和余弦距离
和余弦距离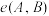 ;
;
(2)若点 ,
,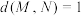 ,求
,求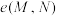 的最大值;
的最大值;
(3)已知点 ,
, 是直线
是直线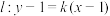 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得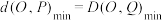 ,若存在,求出所有满足条件的直线
,若存在,求出所有满足条件的直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
 ,
, ,则欧几里得距离
,则欧几里得距离 ;曼哈顿距离
;曼哈顿距离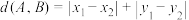 ,余弦距离
,余弦距离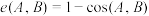 ,其中
,其中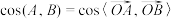 (
( 为坐标原点).
为坐标原点).(1)若
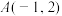 ,
,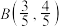 ,求
,求 ,
, 之间的曼哈顿距离
之间的曼哈顿距离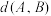 和余弦距离
和余弦距离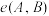 ;
;(2)若点
 ,
,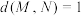 ,求
,求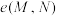 的最大值;
的最大值;(3)已知点
 ,
, 是直线
是直线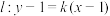 上的两动点,问是否存在直线
上的两动点,问是否存在直线 使得
使得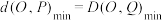 ,若存在,求出所有满足条件的直线
,若存在,求出所有满足条件的直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
您最近一年使用:0次
2024-07-11更新
|
1758次组卷
|
14卷引用:上海市建平中学2023-2024学年高一下学期期末教学质量检测数学试题
上海市建平中学2023-2024学年高一下学期期末教学质量检测数学试题福建省三明市宁化滨江实验中学2024-2025学年高二上学期暑期检测数学试题(已下线)压轴题07 直线的方程和圆的方程的5大题型-【常考压轴题】(人教B版2019选择性必修第一册)河南省开封市龙亭区河南大学附属中学2024-2025学年高二上学期10月月考数学试题福建省南安市侨光中学2024-2025学年高二上学期第1次阶段考试(10月)数学试题福建省厦门大学附属科技中学2024-2025学年高二上学期10月阶段性检测数学试题福建省厦门集美中学2025届高三上学期十月月考数学试卷重庆市重点中学2024-2025学年高二上学期10月月考数学试题安徽省亳州市第二完全中学2024-2025学年高二上学期第一次月考数学试卷云南省玉溪市新平彝族傣族自县民族中学2024-2025学年高二上学期10月期中考试数学试题河南省新乡市河南师范大学附属中学2024-2025学年高二上学期10月月考数学试卷四川省遂宁市射洪中学校2024-2025学年高二上学期强基班第一次月考数学试题北京市大峪中学2024-2025学年高二上学期期中考试数学试题江苏省扬州市第一中学2024-2025学年高二上学期10月教学质量调研评估数学试卷
名校
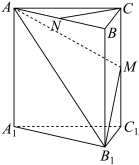
3 . 空间的弯曲性是几何研究的重要内容,用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于 与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有3个面角,每个面角均为
与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有3个面角,每个面角均为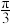 ,故其各个顶点的曲率均为
,故其各个顶点的曲率均为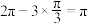 .如图,在直三棱柱
.如图,在直三棱柱 中,点
中,点 的曲率为
的曲率为 ,
, ,
, 分别为
分别为 ,
, 的中点,且
的中点,且 .
.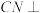 平面
平面 ;
;
(2)若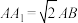 ,求二面角
,求二面角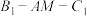 的余弦值;
的余弦值;
(3)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率(多面体有顶点的曲率之和)是常数.
.利用此定理试证明:简单多面体的总曲率(多面体有顶点的曲率之和)是常数.
 与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有3个面角,每个面角均为
与多面体在该点的面角之和的差,其中多面体的面的内角叫做多面体的面角,角度用弧度制.例如:正四面体每个顶点均有3个面角,每个面角均为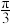 ,故其各个顶点的曲率均为
,故其各个顶点的曲率均为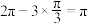 .如图,在直三棱柱
.如图,在直三棱柱 中,点
中,点 的曲率为
的曲率为 ,
, ,
, 分别为
分别为 ,
, 的中点,且
的中点,且 .
.
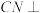 平面
平面 ;
;(2)若
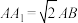 ,求二面角
,求二面角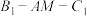 的余弦值;
的余弦值;(3)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为
 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率(多面体有顶点的曲率之和)是常数.
.利用此定理试证明:简单多面体的总曲率(多面体有顶点的曲率之和)是常数.
您最近一年使用:0次
2024-07-07更新
|
1112次组卷
|
4卷引用:湖南省长沙市长郡中学2023-2024学年高一下学期期末考试数学试题
湖南省长沙市长郡中学2023-2024学年高一下学期期末考试数学试题福建省部分学校教学联盟2023~2024学年高一下学期期末质量检测数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2湖北省襄阳市第五中学2024-2025学年高二上学期开学考试数学试题
名校
4 . 由若干个平面多边形围成的几何体叫做多面体,围成多面体的各个多边形叫做多面体的面,两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.对于凸多面体,有著名的欧拉公式: ,其中
,其中 为顶点数,
为顶点数, 为棱数,
为棱数, 为面数.我们可以通过欧拉公式计算立体图形的顶点、棱、面之间的一些数量关系.例如,每个面都是四边形的凸六面体,我们可以确定它的顶点数和棱数.一方面,每个面有4条边,六个面相加共24条边;另一方面,每条棱出现在两个相邻的面中,因此每条棱恰好被计算了两次,即共有12条棱;再根据欧拉公式,
为面数.我们可以通过欧拉公式计算立体图形的顶点、棱、面之间的一些数量关系.例如,每个面都是四边形的凸六面体,我们可以确定它的顶点数和棱数.一方面,每个面有4条边,六个面相加共24条边;另一方面,每条棱出现在两个相邻的面中,因此每条棱恰好被计算了两次,即共有12条棱;再根据欧拉公式, ,可以得到顶点数
,可以得到顶点数 .
.
(1)已知足球是凸三十二面体,每个面均为正五边形或者正六边形,每个顶点与三条棱相邻,试确定足球的棱数;
(2)证明: 个顶点的凸多面体,至多有
个顶点的凸多面体,至多有 条棱;
条棱;
(3)已知正多面体的各个表面均为全等的正多边形,且与每个顶点相邻的棱数均相同.试利用欧拉公式,讨论正多面体棱数的所有可能值.
 ,其中
,其中 为顶点数,
为顶点数, 为棱数,
为棱数, 为面数.我们可以通过欧拉公式计算立体图形的顶点、棱、面之间的一些数量关系.例如,每个面都是四边形的凸六面体,我们可以确定它的顶点数和棱数.一方面,每个面有4条边,六个面相加共24条边;另一方面,每条棱出现在两个相邻的面中,因此每条棱恰好被计算了两次,即共有12条棱;再根据欧拉公式,
为面数.我们可以通过欧拉公式计算立体图形的顶点、棱、面之间的一些数量关系.例如,每个面都是四边形的凸六面体,我们可以确定它的顶点数和棱数.一方面,每个面有4条边,六个面相加共24条边;另一方面,每条棱出现在两个相邻的面中,因此每条棱恰好被计算了两次,即共有12条棱;再根据欧拉公式, ,可以得到顶点数
,可以得到顶点数 .
.(1)已知足球是凸三十二面体,每个面均为正五边形或者正六边形,每个顶点与三条棱相邻,试确定足球的棱数;
(2)证明:
 个顶点的凸多面体,至多有
个顶点的凸多面体,至多有 条棱;
条棱;(3)已知正多面体的各个表面均为全等的正多边形,且与每个顶点相邻的棱数均相同.试利用欧拉公式,讨论正多面体棱数的所有可能值.
您最近一年使用:0次
2024-05-04更新
|
1056次组卷
|
7卷引用:浙江省杭州第二中学2023-2024学年高一下学期期中考试数学试卷
浙江省杭州第二中学2023-2024学年高一下学期期中考试数学试卷(已下线)6.1基本立体图形-【帮课堂】(北师大版2019必修第二册)(已下线)专题6 以新定义为背景的相关问题【讲】(高一期末压轴专项)云南省曲靖市2023-2024学年高二下学期学业水平检测数学试题(已下线)专题4 立体几何中的新定义压轴大题(一)【讲】广东省惠州市第一中学2024-2025学年高二上学期9月阶段考试数学试题广东省佛山市南海区桂城中学2024-2025学年高二上学期级第一次段考数学试卷
名校
解题方法
5 . 近些年来,三维扫描技术得到空前发展,从而催生了数字几何这一新兴学科.数字几何是传统几何和计算机科学相结合的产物.数字几何中的一个重要概念是曲率,用曲率来刻画几何体的弯曲程度.规定:多面体在顶点处的曲率等于 与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有
与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有 个面角,每个面角是
个面角,每个面角是 ,所以正方体在各顶点的曲率为
,所以正方体在各顶点的曲率为  ,故其总曲率为
,故其总曲率为 .
.
(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率是常数.
.利用此定理试证明:简单多面体的总曲率是常数.
 与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有
与多面体在该点的所有面角之和的差(多面体的面角是指多面体的面上的多边形的内角的大小,用弧度制表示),多面体在面上非顶点处的曲率均为零.由此可知,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正方体在每个顶点有 个面角,每个面角是
个面角,每个面角是 ,所以正方体在各顶点的曲率为
,所以正方体在各顶点的曲率为  ,故其总曲率为
,故其总曲率为 .
.(1)求四棱锥的总曲率;
(2)表面经过连续变形可以变为球面的多面体称为简单多面体.关于简单多面体有著名欧拉定理:设简单多面体的顶点数为
 ,棱数为
,棱数为 ,面数为
,面数为 ,则有:
,则有: .利用此定理试证明:简单多面体的总曲率是常数.
.利用此定理试证明:简单多面体的总曲率是常数.
您最近一年使用:0次
2022-09-19更新
|
1154次组卷
|
9卷引用:2022年浙江省温州市摇篮杯高一数学竞赛试题
2022年浙江省温州市摇篮杯高一数学竞赛试题(已下线)8.1 基本立体图形2(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)(已下线)专题14 棱柱、棱锥和棱台-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题6 以新定义为背景的相关问题【练】(高一期末压轴专项)(已下线)第01讲 空间几何体的结构、三视图和直观图与空间几何体的表面积和体积(练)(已下线)第五篇 向量与几何 专题21 曲率与曲率圆 微点3 曲率与曲率圆综合训练(已下线)11.2 锥体(第1课时)(七大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)(已下线)第八章立体几何8.1 空间几何体及其表面积与体积(已下线)专题4 立体几何中的新定义压轴大题(过关集训)



