解题方法
1 . 如图,平面内的两条相交直线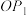 和
和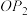 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若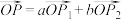 ,且点
,且点 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数 、
、 满足( )
满足( )
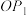 和
和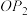 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若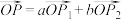 ,且点
,且点 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数 、
、 满足( )
满足( )
A. , , ; ; | B. , , ; ; |
C. , , ; ; | D. , , . . |
您最近一年使用:0次
2024-08-07更新
|
79次组卷
|
2卷引用:【课堂例】8.3.1 向量基本定理 课堂例题 沪教版(2020)必修第二册第8章 平面向量
2 . 下列函数中在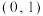 上为严格减函数的是( )
上为严格减函数的是( )
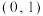 上为严格减函数的是( )
上为严格减函数的是( )A.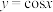 ; ; | B. ; ; | C. ; ; | D. . . |
您最近一年使用:0次
解题方法
3 . 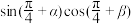 化为和差的结果是( )
化为和差的结果是( )
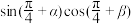 化为和差的结果是( )
化为和差的结果是( )A. ; ; | B. ; ; |
C.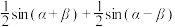 ; ; | D.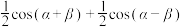 . . |
您最近一年使用:0次
4 . 函数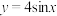 的图象关于( ).
的图象关于( ).
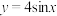 的图象关于( ).
的图象关于( ).| A.y轴对称; | B.直线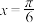 对称; 对称; |
| C.原点对称; | D.直线 对称. 对称. |
您最近一年使用:0次
5 . 已知函数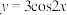 的定义域为
的定义域为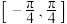 ,值域为
,值域为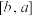 ,那么
,那么 的值为( ).
的值为( ).
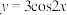 的定义域为
的定义域为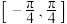 ,值域为
,值域为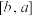 ,那么
,那么 的值为( ).
的值为( ).| A.-6 | B.-3 | C. | D. |
您最近一年使用:0次
6 . 已知函数 ,其中
,其中 ,则下列命题中正确的是( ).
,则下列命题中正确的是( ).
 ,其中
,其中 ,则下列命题中正确的是( ).
,则下列命题中正确的是( ).A. 是最小正周期为1的函数; 是最小正周期为1的函数; |
B. 是最小正周期为2的函数; 是最小正周期为2的函数; |
C. 是最小正周期为 是最小正周期为 的函数; 的函数; |
D. 是最小正周期为 是最小正周期为 的函数. 的函数. |
您最近一年使用:0次
解题方法
7 . 共点力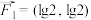 ,
,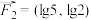 作用在物体M上,产生位移
作用在物体M上,产生位移 ,则共点力对物体做的功为( ).
,则共点力对物体做的功为( ).
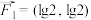 ,
,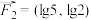 作用在物体M上,产生位移
作用在物体M上,产生位移 ,则共点力对物体做的功为( ).
,则共点力对物体做的功为( ).A. | B.lg5 | C.1 | D.2 |
您最近一年使用:0次
解题方法
8 . 若等腰三角形的底角的正弦值为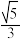 ,则顶角的余弦值为( ).
,则顶角的余弦值为( ).
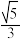 ,则顶角的余弦值为( ).
,则顶角的余弦值为( ).A.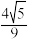 ; ; | B.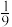 ; ; | C.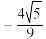 ; ; | D.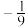 . . |
您最近一年使用:0次
9 . 现有以下两个命题:
①存在角α和β,使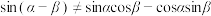 ;
;
②存在角α和β,使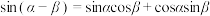 ;
;
则判断正确的是( ).
①存在角α和β,使
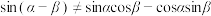 ;
;②存在角α和β,使
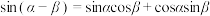 ;
;则判断正确的是( ).
| A.①②均正确; | B.①②均错误; | C.①对②错; | D.①错②对. |
您最近一年使用:0次
解题方法
10 . 如图,梯子(长度不变)跟地面所成的锐角为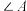 ,关于
,关于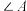 的三角函数值与梯子的倾斜程度之间,下列说法正确的是( ).
的三角函数值与梯子的倾斜程度之间,下列说法正确的是( ).
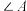 ,关于
,关于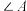 的三角函数值与梯子的倾斜程度之间,下列说法正确的是( ).
的三角函数值与梯子的倾斜程度之间,下列说法正确的是( ).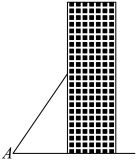
A.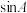 的值越大,梯子越陡; 的值越大,梯子越陡; |
B. 的值越大,梯子越陡; 的值越大,梯子越陡; |
C.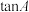 的值越小,梯子越陡; 的值越小,梯子越陡; |
D.陡缓程度与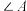 的三角函数值无关. 的三角函数值无关. |
您最近一年使用:0次



