名校
1 . 某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产 万件,需另投入流动成本
万件,需另投入流动成本 万元,当年产量小于
万元,当年产量小于 万件时,
万件时, (万元);当年产量不小于
(万元);当年产量不小于 万件时,
万件时, (万元).已知每件产品售价为
(万元).已知每件产品售价为 元,假若该同学生产的商品当年能全部售完.
元,假若该同学生产的商品当年能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?(取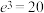 ).
).
 万件,需另投入流动成本
万件,需另投入流动成本 万元,当年产量小于
万元,当年产量小于 万件时,
万件时, (万元);当年产量不小于
(万元);当年产量不小于 万件时,
万件时, (万元).已知每件产品售价为
(万元).已知每件产品售价为 元,假若该同学生产的商品当年能全部售完.
元,假若该同学生产的商品当年能全部售完.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?(取
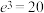 ).
).
您最近一年使用:0次
2020-11-19更新
|
1815次组卷
|
40卷引用:浙江省浦江中学、长兴中学、余杭高中三校2021-2022学年高二下学期3月联考数学试题
浙江省浦江中学、长兴中学、余杭高中三校2021-2022学年高二下学期3月联考数学试题山东省济宁市嘉祥一中2019-2020学期高二下学期期中模块测试数学试题江西省新余市第一中学2019-2020学年高二下学期第一次段考数学(理)试题河北省枣强中学2019-2020学年高二下学期期中数学试题(已下线)3.4+生活中的优化问题举例(重点练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-1)(已下线)专题25 一元函数的导数及其应用(单元测试卷)-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练山西省太原市第五中学2020-2021学年高二下学期4月阶段性检测数学(理)试题(已下线)1.4 生活中的优化问题举例(重点练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)河南省洛阳市豫西名校2020-2021学年高二下学期第一次联考理科数学试题(已下线)第08章:《期末综合试卷一》 (B卷提升篇)- 2020-2021学年高二下学期数学期末考点大串讲(苏教版)吉林省梅河口市第五中学2020-2021学年高二下学期期末考试数学(文)试题吉林省梅河口市第五中学2020-2021学年高二下学期期末考试数学(理)试题江苏省南通市如皋中学2020-2021学年高二下学期第一次阶段考试数学试题陕西省宝鸡市千阳县中学2019-2020学年高二下学期期中理科数学试题广东省佛山市顺德区十一校联盟2020-2021学年高二下学期第二次段考数学试题福建省福鼎第一中学2021-2022学年高二下学期第一次月考数学试题广东省仁化县仁化中学2021-2022学年高二下学期期中数学试题辽宁省沈阳市第一二〇中学2021-2022学年高二下学期第三次考试数学试题广西玉林市第十一中学2021-2022学年高二下学期3月月考数学试题(理科)山东省威海市乳山市银滩高级中学2022-2023学年高二下学期6月月考数学试题江苏省锡东高级中学2023-2024学年高二下学期3月阶段性考试数学试题四川省仁寿第一中学校(北校区)2023-2024学年高二下学期3月月考数学试题安徽省淮南第二中学2023-2024学年高二下学期期中教学检测数学试题【市级联考】山东省临沂市2019届高三上学期期中考试数学理试题江苏省泰州中学、江都中学、宜兴中学2019-2020学年高三上学期11月月考数学试题(已下线)专题15 以导数为背景的应用题-《巅峰冲刺2020年高考之二轮专项提升》(江苏)2020届河北省衡水中学高三年级小二调考试数学理科试卷2020届河北省衡水中学高三年级小二调考试数学文科试卷江苏省泰州中学、江都中学、宜兴中学2019-2020学年高三上学期10月月考数学试题(已下线)考点12 导数的应用-备战2021年高考数学(理)一轮复习考点一遍过(已下线)考点12 导数的应用-备战2021年高考数学(文)一轮复习考点一遍过宁夏银川一中2021届高三上学期第二次月考数学(文)试题宁夏银川一中2021届高三上学期第二次月考数学(理)试题宁夏银川一中2021届高三第二次月考理科数学试题湖南省邵阳市邵东创新实验学校2020-2021学年高三上学期10月月考数学试题安徽省安庆市怀宁中学2020-2021学年高三上学期第一次质量检测理科数学试题宁夏隆德县中学2021届高三年级上学期第三次月考数学(理)试题广东省佛山市第一中学2021届高三上学期九月月考数学试题甘肃省兰州第一中学2022-2023学年高三上学期期中考试数学(理)试题河南省郑州外国语学校2023届高三上学期第二次调研数学试题
2 . 某批发商以每吨20元的价格购进一批建筑材料,若以每吨M元零售,销量N(单位:吨)与零售价M(单位:元)有如下关系: ,则该批材料零售价定为
,则该批材料零售价定为_______ 元时利润最大,利润的最大值为_________ 元.
 ,则该批材料零售价定为
,则该批材料零售价定为
您最近一年使用:0次
2020-12-03更新
|
437次组卷
|
4卷引用:专题5.4 《一元函数的导数及其应用》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版,浙江专用)
(已下线)专题5.4 《一元函数的导数及其应用》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版,浙江专用)人教A版(2019) 选择性必修第二册 过关斩将 第五章 一元函数的导数及其应用 5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第2课时 函数的最大(小)值(已下线)专题12 导数在函数有关问题及实际生活中的应用 核心素养练习 -【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第二册)广东省佛山市实验中学2020-2021学年高二下学期阶段考试(一)数学试题
名校
3 . 你是否注意过,市场上等量的小包装的物品一般比大包装的要贵一些?高二某研究小组针对饮料瓶的大小对饮料公司利润的影响进行了研究,调查如下:某制造商制造并出售球形瓶装的某种饮料,瓶子的制造成本是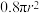 分,其中r(单位:cm)是瓶子的半径.已知每出售1mL的饮料,制造商可获利0.2分(不考虑瓶子的成本的前提下),且制造商能制作的瓶子的最大半径为6cm.下面结论正确的有( )(注:
分,其中r(单位:cm)是瓶子的半径.已知每出售1mL的饮料,制造商可获利0.2分(不考虑瓶子的成本的前提下),且制造商能制作的瓶子的最大半径为6cm.下面结论正确的有( )(注: ;利润可为负数)
;利润可为负数)
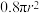 分,其中r(单位:cm)是瓶子的半径.已知每出售1mL的饮料,制造商可获利0.2分(不考虑瓶子的成本的前提下),且制造商能制作的瓶子的最大半径为6cm.下面结论正确的有( )(注:
分,其中r(单位:cm)是瓶子的半径.已知每出售1mL的饮料,制造商可获利0.2分(不考虑瓶子的成本的前提下),且制造商能制作的瓶子的最大半径为6cm.下面结论正确的有( )(注: ;利润可为负数)
;利润可为负数)| A.利润随着瓶子半径的增大而增大 | B.半径为6cm时,利润最大 |
| C.半径为2cm时,利润最小 | D.半径为3cm时,制造商不获利 |
您最近一年使用:0次
2023-10-14更新
|
400次组卷
|
5卷引用:浙江省宁波市余姚中学2023-2024学年高二上学期第一次质量检测数学试题
浙江省宁波市余姚中学2023-2024学年高二上学期第一次质量检测数学试题(已下线)专题04 函数的极值与最大(小)值 (十二大考点)-【寒假自学课】2024年高二数学寒假提升学与练(人教A版2019)(已下线)6.3利用导数解决实际问题(分层练习,5大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)第5.3.2讲 利用导数求解函数的综合问题(第3课时)-2023-2024学年高二数学同步精讲精练宝典(人教A版2019选修第二、三册)(已下线)2.7导数的应用(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)
名校
解题方法
4 . 某厂生产某种产品x件的总成本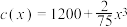 (万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,问产量定为多少时,总利润最大?(总利润
(万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,问产量定为多少时,总利润最大?(总利润 总销售额
总销售额 总成本)
总成本)
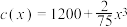 (万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,问产量定为多少时,总利润最大?(总利润
(万元),已知产品单价的平方与产品件数x成反比,生产100件这样的产品单价为50万元,问产量定为多少时,总利润最大?(总利润 总销售额
总销售额 总成本)
总成本)
您最近一年使用:0次
2023-04-14更新
|
213次组卷
|
2卷引用:浙江省杭州市第四中学吴山校区2022-2023学年高二下学期期中数学试题
解题方法
5 . 某工厂共有10台机器共同生产一种仪器的元件,由于受生产能力和技术水平等因素的影响,会产生一定数量的次品.根据经验知道,每台机器生产的次品数 (万件)与每台机器的日产量
(万件)与每台机器的日产量 (万件)之间满足关系:
(万件)之间满足关系: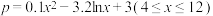 ,已知每生产1万件合格的元件可盈利2万元,但每生产1万件次品将亏损1万元.
,已知每生产1万件合格的元件可盈利2万元,但每生产1万件次品将亏损1万元.
(1)试将该工厂每天生产这种元件所获得的利润 (万元)表示为关于
(万元)表示为关于 (万件)的函数(利润
(万件)的函数(利润 盈利
盈利 亏损);
亏损);
(2)当每台机器的日产量 (万件)为多少时,获得的利润最大,最大利润为多少?
(万件)为多少时,获得的利润最大,最大利润为多少?
 (万件)与每台机器的日产量
(万件)与每台机器的日产量 (万件)之间满足关系:
(万件)之间满足关系: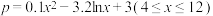 ,已知每生产1万件合格的元件可盈利2万元,但每生产1万件次品将亏损1万元.
,已知每生产1万件合格的元件可盈利2万元,但每生产1万件次品将亏损1万元.(1)试将该工厂每天生产这种元件所获得的利润
 (万元)表示为关于
(万元)表示为关于 (万件)的函数(利润
(万件)的函数(利润 盈利
盈利 亏损);
亏损);(2)当每台机器的日产量
 (万件)为多少时,获得的利润最大,最大利润为多少?
(万件)为多少时,获得的利润最大,最大利润为多少?
您最近一年使用:0次
名校
6 . 某学校高二年级一个学习兴趣小组进行社会实践活动,决定对某“著名品牌” 系列进行市场销售量调研,通过对该品牌的
系列进行市场销售量调研,通过对该品牌的 系列一个阶段的调研得知,发现
系列一个阶段的调研得知,发现 系列每日的销售量
系列每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (元/千克)近似满足关系式
(元/千克)近似满足关系式 ,其中
,其中 ,
, 为常数.已知销售价格为6元/千克时,每日可售出
为常数.已知销售价格为6元/千克时,每日可售出 系列15千克.
系列15千克.
(1)求函数 的解析式;
的解析式;
(2)若 系列的成本为4元/千克,试确定销售价格
系列的成本为4元/千克,试确定销售价格 的值,使该商场每日销售
的值,使该商场每日销售 系列所获得的利润最大.
系列所获得的利润最大.
 系列进行市场销售量调研,通过对该品牌的
系列进行市场销售量调研,通过对该品牌的 系列一个阶段的调研得知,发现
系列一个阶段的调研得知,发现 系列每日的销售量
系列每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (元/千克)近似满足关系式
(元/千克)近似满足关系式 ,其中
,其中 ,
, 为常数.已知销售价格为6元/千克时,每日可售出
为常数.已知销售价格为6元/千克时,每日可售出 系列15千克.
系列15千克.(1)求函数
 的解析式;
的解析式;(2)若
 系列的成本为4元/千克,试确定销售价格
系列的成本为4元/千克,试确定销售价格 的值,使该商场每日销售
的值,使该商场每日销售 系列所获得的利润最大.
系列所获得的利润最大.
您最近一年使用:0次
2018-06-30更新
|
2887次组卷
|
14卷引用:浙江省山河联盟2022-2023学年高二下学期3月联考数学试题
浙江省山河联盟2022-2023学年高二下学期3月联考数学试题【全国市级联考】江苏省宿迁市2017-2018学年高二下学期期末考试数学(文)试题(已下线)3.4+生活中的优化问题举例(基础练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-1)(已下线)1.4 生活中的优化问题举例(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)江西省新余市2020-2021学年高二下学期期末数学(文)试题人教B版(2019) 选修第三册 名师精选 第九单元 导数在研究函数中的应用、导数的实际应用(已下线)章节综合测试-导数第五章 一元函数的导数及其应用 (单元测)福建省连城县第一中学2022-2023学年高二下学期3月月考数学试题四川省江油市太白中学2022-2023学年高二下学期3月月考文科数学试题重庆市长寿中学校2022-2023学年高二下学期期中数学试题(已下线)2.7导数的应用(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)广东省东莞市第七高级中学2023-2024学年高二下学期数学第一次月考数学试题(已下线)模块四 期中重组篇(人教B版高二下重庆)



