解题方法
1 . 北京市共有16个行政区,东城区、西城区、朝阳区、丰台区、石景山区和海淀区为中心城区,其他为非中心城区.根据《北京市人口蓝皮书・北京人口发展研究报告(2023)》显示,2022年北京市常住人口为2184.3万人,由城镇人口和乡村人口两个部分构成,各区常住人口数量如下表所示:
(1)在16个行政区中随机选择一个,求该区为非中心城区且2022年乡村人口在20万人以下的概率;
(2)若随机从中心城区选取1个,非中心城区选取2个行政区,记选出的3个区中2022年常住人口超过100万人的行政区的个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ;
;
(3)记2022年这16个区的常住人口、城镇人口、乡村人口的方差分别为 ,
, ,
,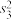 .试判断
.试判断 ,
, ,
,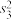 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
| 行政区 | 东城区 | 西城区 | 朝阳区 | 丰台区 | 石景山区 | 海淀区 | 门头沟区 | 房山区 |
| 城镇人口(万人) | 70.4 | 110 | 343.3 | 199.9 | 56.3 | 305.4 | 36.2 | 102.6 |
| 乡村人口(万人) | 0 | 0 | 0.9 | 1.3 | 0 | 7 | 3.4 | 28.5 |
| 行政区 | 通州区 | 顺义区 | 昌平区 | 大兴区 | 怀柔区 | 平谷区 | 密云区 | 延庆区 |
| 城镇人口(万人) | 137.3 | 87.8 | 185.9 | 161.6 | 32.8 | 27.9 | 34.9 | 20.5 |
| 乡村人口(万人) | 47 | 44.7 | 40.8 | 37.5 | 11.1 | 17.7 | 17.7. | 13.9 |
(2)若随机从中心城区选取1个,非中心城区选取2个行政区,记选出的3个区中2022年常住人口超过100万人的行政区的个数为
 ,求
,求 的分布列及数学期望
的分布列及数学期望 ;
;(3)记2022年这16个区的常住人口、城镇人口、乡村人口的方差分别为
 ,
, ,
,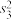 .试判断
.试判断 ,
, ,
,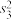 的大小关系.(结论不要求证明)
的大小关系.(结论不要求证明)
您最近一年使用:0次
名校
解题方法
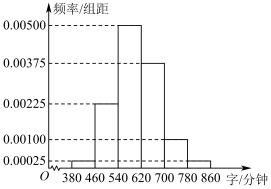
2 . 某中学为了解本校高二年级学生阅读水平现状,从该年级学生中随机抽取100人进行一般现代文阅读速度的测试,以每位学生平均每分钟阅读的字数作为该学生的阅读速度,将测试结果整理得到如下频率分布直方图:
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,求
,求 的分布列与数学期望
的分布列与数学期望 ;
;
(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的 的大小.
的大小.
(2)用频率估计概率,从该校高二学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,求
,求 的分布列与数学期望
的分布列与数学期望 ;
;(3)若某班有10名学生参加测试,他们的阅读速度如下:506,516,553,592,617,632,667,693,723,776,从这10名学生中随机抽取3人,设这3人中阅读速度达到540字/分钟及以上的人数为
 ,试判断数学期望
,试判断数学期望 与(2)中的
与(2)中的 的大小.
的大小.
您最近一年使用:0次
2024-05-08更新
|
1385次组卷
|
11卷引用:北京市东城区2023-2024学年高三下学期综合练习(一)(一模)数学试题
北京市东城区2023-2024学年高三下学期综合练习(一)(一模)数学试题(已下线)8.4 离散型随机变量的分布列,期望与方差(高考真题素材之十年高考)(已下线)模型4 以超几何分布为背景的离散型随机变量问题模型(第9章 计数原理、概率、随机变量及其分布 )(已下线)第七章:随机变量及其分布(单元测试,新题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)安徽省安庆市第一中学2023-2024学年高二下学期第一次阶段性检测(期中)数学试题吉林省白山市抚松县第一中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题07 概率与统计综合问题(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)北京市鲁迅中学2023-2024学年高二下学期期中测试数学试卷
名校
解题方法
3 . 已知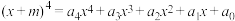 ,若
,若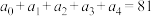 ,则
,则 的取值可以为( )
的取值可以为( )
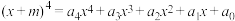 ,若
,若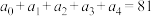 ,则
,则 的取值可以为( )
的取值可以为( )| A.2 | B.1 | C. | D. |
您最近一年使用:0次
2024-04-08更新
|
2165次组卷
|
7卷引用:北京市东城区2023-2024学年高三下学期综合练习(一)(一模)数学试题
北京市东城区2023-2024学年高三下学期综合练习(一)(一模)数学试题湖南省长沙市第一中学2024届高三下学期模拟试卷(二)数学试题安徽省六安市霍山文峰学校2024届高三最后一卷数学试卷(已下线)第二节 二项式定理【同步课时】北京专项(已下线)模块五 专题3 全真能力模拟3(苏教版高二期中研习)北京市第八十中学2023-2024学年高二下学期期中考试数学试题北京市第一六六中学2023-2024学年高二下学期期中考试数学试题
名校
解题方法
4 . 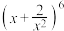 的展开式中的常数项为
的展开式中的常数项为___________ (用数字填写答案).
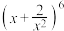 的展开式中的常数项为
的展开式中的常数项为
您最近一年使用:0次
2024-02-17更新
|
1121次组卷
|
12卷引用:2020届北京市东城区高三一模考试数学试题
2020届北京市东城区高三一模考试数学试题2019年上海市奉贤区高三4月调研测试(二模)数学试题2017年上海市青浦区高三上学期期末质量调研(一模)数学试题(已下线)上海市华东师范大学第二附属中学2016-2017学年高三上学期12月月考数学试题2020届上海市崇明区高三第一次高考模拟数学试题贵州省部分重点中学2019届高三上学期高考教学质量评测卷(四)(期末)数学(理)试题2020届河南省郑州市高三第二次质量预测理科数学试题福建省泉州市晋江二中、鹏峰中学、广海中学、泉港五中2023届高三上学期10月期中联考数学试题湖北省高中名校联盟2024届高三第三次联考综合测评数学试卷四川省巴中市普通高中2024届高三“一诊”考试理科数学试题(已下线)第1讲:二项式定理和二项分布的最值问题【讲】河北省沧州市第一中学2020-2021学年高二下学期开学考试数学试题
名校
解题方法
5 . 某科目进行考试时,从计算机题库中随机生成一份难度相当的试卷.规定每位同学有三次考试机会,一旦某次考试通过,该科目成绩合格,无需再次参加考试,否则就继续参加考试,直到用完三次机会.现从2022年和2023年这两年的第一次、第二次、第三次参加考试的考生中,分别随机抽取100位考生,获得数据如下表:
假设每次考试是否通过相互独立.
(1)从2022年和2023年第一次参加考试的考生中各随机抽取一位考生,估计这两位考生都通过考试的概率;
(2)小明在2022年参加考试,估计他不超过两次考试该科目成绩合格的概率;
(3)若2023年考生成绩合格的概率不低于2022年考生成绩合格的概率,则 的最小值为下列数值中的哪一个?(直接写出结果)
的最小值为下列数值中的哪一个?(直接写出结果)
| 2022年 | 2023年 | |||
| 通过 | 未通过 | 通过 | 未通过 | |
| 第一次 | 60人 | 40人 | 50人 | 50人 |
| 第二次 | 70人 | 30人 | 60人 | 40人 |
| 第三次 | 80人 | 20人 |  人 人 | 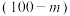 人 人 |
(1)从2022年和2023年第一次参加考试的考生中各随机抽取一位考生,估计这两位考生都通过考试的概率;
(2)小明在2022年参加考试,估计他不超过两次考试该科目成绩合格的概率;
(3)若2023年考生成绩合格的概率不低于2022年考生成绩合格的概率,则
 的最小值为下列数值中的哪一个?(直接写出结果)
的最小值为下列数值中的哪一个?(直接写出结果) 的值 的值 | 83 | 88 | 93 |
您最近一年使用:0次
2024-01-19更新
|
1082次组卷
|
5卷引用:北京市东城区2024届高三上学期期末统一检测数学试题
北京市东城区2024届高三上学期期末统一检测数学试题广东省广州市培正中学2024届高三上学期第一次模拟测试数学试题(已下线)模块八 概率与统计(测试)北京市第一○一中学2025届高三上学期开学检测数学试题(已下线)第七章 随机变量及其分布(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)
名校
6 . 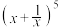 的展开式中,
的展开式中, 的系数为( )
的系数为( )
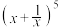 的展开式中,
的展开式中, 的系数为( )
的系数为( )| A.1 | B.5 | C.10 | D.20 |
您最近一年使用:0次
2024-01-19更新
|
687次组卷
|
4卷引用:北京市东城区2024届高三上学期期末统一检测数学试题
北京市东城区2024届高三上学期期末统一检测数学试题(已下线)高三数学开学摸底考 (北京专用)(已下线)2024年高考数学二轮复习测试卷(全国卷理科专用)北京市门头沟区大峪中学2023-2024学年高二下学期开学考试数学试题
名校
解题方法
7 . 已知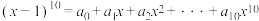 ,则
,则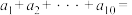 ( )
( )
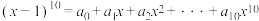 ,则
,则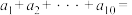 ( )
( )A.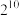 | B.0 | C.1 | D. |
您最近一年使用:0次
2024-01-12更新
|
505次组卷
|
4卷引用:北京市第十一中学2023届高三三模(5月)数学试题
名校
8 . 二项式 的展开式中常数项为
的展开式中常数项为 __________ .(用数字作答)
 的展开式中常数项为
的展开式中常数项为
您最近一年使用:0次
2023-12-22更新
|
905次组卷
|
4卷引用:北京市东城区景山学校2024届高三上学期12月月考数学试题
北京市东城区景山学校2024届高三上学期12月月考数学试题北京市东城区2023-2024学年高三下学期综合练习(二)(二模)数学试题(已下线)第04讲 6.3.1二项式定理+6.3.2二项式系数的性质(1)重庆市重庆市长寿区重庆市长寿川维中学校2023-2024学年高二下学期5月月考数学试题
名校
解题方法
9 . 不粘锅是家庭常用的厨房用具,近期,某市消费者权益保护委员会从市场上购买了12款不粘锅商品,并委托第三方检测机构进行检测,本次选取了食物接触材料安全项目中与消费者使用密切相关的6项性能项目进行比较试验,性能检测项目包含不粘性、耐磨性、耐碱性、手柄温度、温度均匀性和使用体验等6个指标.其中消费者关注最多的两个指标“不沾性、耐磨性”检测结果的数据如下:
(Ⅰ级代表性能优秀,Ⅱ级代表性能较好)
(1)从这12个品牌的样本数据中随机选取两个品牌的数据,求这两个品牌的“不粘性”性能都是Ⅰ级的概率:
(2)从前六个品牌、后六个品牌中各随机选取两个品牌的数据,求两个指标“不沾性、耐磨性”都是Ⅰ级的品牌个数恰为2个的概率;
(3)顾客甲从品牌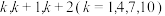 中随机选取1个品牌,用“
中随机选取1个品牌,用“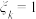 ”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“
”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“ ”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差
”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差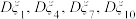 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).
检测结果 | 检测结果 | |||||||
序号 | 品牌名称 | 不粘性 | 耐磨性 | 序号 | 品牌名称 | 不粘性 | 耐磨性 | |
1 | 品牌1 | Ⅰ级 | Ⅰ级 | 7 | 品牌7 | Ⅰ级 | Ⅰ级 | |
2 | 品牌2 | Ⅱ级 | Ⅰ级 | 8 | 品牌8 | Ⅰ级 | Ⅰ级 | |
3 | 品牌3 | Ⅰ级 | Ⅰ级 | 9 | 品牌9 | Ⅱ级 | Ⅱ级 | |
4 | 品牌4 | Ⅱ级 | Ⅱ级 | 10 | 品牌10 | Ⅱ级 | Ⅱ级 | |
5 | 品牌5 | Ⅰ级 | Ⅰ级 | 11 | 品牌11 | Ⅱ级 | Ⅱ级 | |
6 | 品牌6 | Ⅱ级 | Ⅰ级 | 12 | 品牌12 | Ⅱ级 | Ⅱ级 | |
(1)从这12个品牌的样本数据中随机选取两个品牌的数据,求这两个品牌的“不粘性”性能都是Ⅰ级的概率:
(2)从前六个品牌、后六个品牌中各随机选取两个品牌的数据,求两个指标“不沾性、耐磨性”都是Ⅰ级的品牌个数恰为2个的概率;
(3)顾客甲从品牌
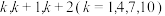 中随机选取1个品牌,用“
中随机选取1个品牌,用“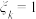 ”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“
”表示选取的品牌两个指标“不沾性、耐磨性”都是Ⅰ级,“ ”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差
”表示选取的品牌两个指标“不沾性、耐磨性”不都是Ⅰ级(k=1,4,7,10).写出方差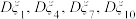 的大小关系(结论不要求证明).
的大小关系(结论不要求证明).
您最近一年使用:0次
2023-12-11更新
|
287次组卷
|
3卷引用:北京市东城区第五十五中学2024届高三上学期12月月考数学试题
北京市东城区第五十五中学2024届高三上学期12月月考数学试题广东省部分学校2025届高三上学期新起点模拟考试数学试题(已下线)专题7.7 随机变量及其分布全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
10 . 在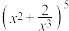 的展开式中,常数项为( )
的展开式中,常数项为( )
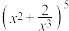 的展开式中,常数项为( )
的展开式中,常数项为( )| A.10 | B.20 | C.40 | D.80 |
您最近一年使用:0次
2023-12-08更新
|
1055次组卷
|
4卷引用:北京市东城区第一七一中学2024届高三上学期12月月考数学试题
北京市东城区第一七一中学2024届高三上学期12月月考数学试题福建省三明市第一中学2024届高三上学期月考二(12月)数学试题(已下线)第六章 计数原理(知识归纳+题型突破)(3)(已下线)专题6.7 计数原理全章综合测试卷(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)



