23-24高三上·北京石景山·期末
名校
解题方法
1 . 某学校体育课进行投篮练习,投篮地点分为 区和
区和 区,每一个球可以选择在
区,每一个球可以选择在 区投篮也可以选择在
区投篮也可以选择在 区投篮,在
区投篮,在 区每投进一球得2分,没有投进得0分;在
区每投进一球得2分,没有投进得0分;在 区每投进一球得3分,没有投进得0分.学生甲在
区每投进一球得3分,没有投进得0分.学生甲在 ,
, 两区的投篮练习情况统计如下表:
两区的投篮练习情况统计如下表:
假设用频率估计概率,且学生甲每次投篮相互独立.
(1)试分别估计甲在 区,
区, 区投篮命中的概率;
区投篮命中的概率;
(2)若甲在 区投
区投 个球,在
个球,在 区投
区投 个球,求甲在
个球,求甲在 区投篮得分高于在
区投篮得分高于在 区投篮得分的概率;
区投篮得分的概率;
(3)若甲在 区,
区, 区一共投篮
区一共投篮 次,投篮得分的期望值不低于
次,投篮得分的期望值不低于 分,直接写出甲选择在
分,直接写出甲选择在 区投篮的最多次数.(结论不要求证明)
区投篮的最多次数.(结论不要求证明)
 区和
区和 区,每一个球可以选择在
区,每一个球可以选择在 区投篮也可以选择在
区投篮也可以选择在 区投篮,在
区投篮,在 区每投进一球得2分,没有投进得0分;在
区每投进一球得2分,没有投进得0分;在 区每投进一球得3分,没有投进得0分.学生甲在
区每投进一球得3分,没有投进得0分.学生甲在 ,
, 两区的投篮练习情况统计如下表:
两区的投篮练习情况统计如下表:甲 |
|
|
投篮次数 |
|
|
得分 |
|
|
(1)试分别估计甲在
 区,
区, 区投篮命中的概率;
区投篮命中的概率;(2)若甲在
 区投
区投 个球,在
个球,在 区投
区投 个球,求甲在
个球,求甲在 区投篮得分高于在
区投篮得分高于在 区投篮得分的概率;
区投篮得分的概率;(3)若甲在
 区,
区, 区一共投篮
区一共投篮 次,投篮得分的期望值不低于
次,投篮得分的期望值不低于 分,直接写出甲选择在
分,直接写出甲选择在 区投篮的最多次数.(结论不要求证明)
区投篮的最多次数.(结论不要求证明)
您最近一年使用:0次
2024-01-22更新
|
541次组卷
|
4卷引用:2024年高考数学二轮复习测试卷(北京专用)
(已下线)2024年高考数学二轮复习测试卷(北京专用)北京市石景山区2024届高三上学期期末数学试题北京市第一六一中学2023-2024学年高三下学期开学测试数学试卷(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(4)
23-24高三上·北京昌平·期末
解题方法
2 . 已知 ,则
,则 ( )
( )
 ,则
,则 ( )
( )A.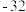 | B.32 | C.495 | D.585 |
您最近一年使用:0次
23-24高三上·广东深圳·阶段练习
名校
3 . 已知某足球赛事的决赛将在甲、乙两队之间进行.其规则为:每一场比赛均须决出胜负,按主、客场制先进行两场比赛(第一场在甲队主场比赛),若某一队在前两场比赛中均获胜,则该队获得冠军;否则,两队需在中立场进行第三场比赛,且其获胜方为冠军.已知甲队在主场、客场、中立场获胜的概率依次为 ,
, ,
, ,且每场比赛的胜负均相互独立.
,且每场比赛的胜负均相互独立.
(1)当甲队获得冠军时,求决赛需进行三场比赛的概率;
(2)若主办方在决赛的前两场中共投资 (千万元),则能在这两场比赛中共盈利
(千万元),则能在这两场比赛中共盈利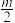 (千万元).如果需进行第三场比赛,且主办方在第三场比赛中投资
(千万元).如果需进行第三场比赛,且主办方在第三场比赛中投资 (千万元),则能在该场比赛中盈利
(千万元),则能在该场比赛中盈利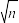 (千万元).若主办方最多能投资一千万元,请以决赛总盈利的数学期望为决策依据,则其在前两场的投资额应为多少万元?
(千万元).若主办方最多能投资一千万元,请以决赛总盈利的数学期望为决策依据,则其在前两场的投资额应为多少万元?
 ,
, ,
, ,且每场比赛的胜负均相互独立.
,且每场比赛的胜负均相互独立.(1)当甲队获得冠军时,求决赛需进行三场比赛的概率;
(2)若主办方在决赛的前两场中共投资
 (千万元),则能在这两场比赛中共盈利
(千万元),则能在这两场比赛中共盈利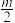 (千万元).如果需进行第三场比赛,且主办方在第三场比赛中投资
(千万元).如果需进行第三场比赛,且主办方在第三场比赛中投资 (千万元),则能在该场比赛中盈利
(千万元),则能在该场比赛中盈利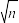 (千万元).若主办方最多能投资一千万元,请以决赛总盈利的数学期望为决策依据,则其在前两场的投资额应为多少万元?
(千万元).若主办方最多能投资一千万元,请以决赛总盈利的数学期望为决策依据,则其在前两场的投资额应为多少万元?
您最近一年使用:0次
2024-01-02更新
|
653次组卷
|
5卷引用:黄金卷07
(已下线)黄金卷07(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)广东省深圳实验、湛江一中、珠海一中三校2024届高三上学期12月联考数学试题山西省朔州市怀仁市2023-2024学年高三上学期第二次教学质量调研数学试题(已下线)7.3.1 离散型随机变量的均值——课后作业(提升版)
23-24高三上·江西九江·阶段练习
4 . 已知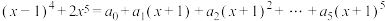 ,则
,则 ( )
( )
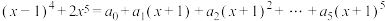 ,则
,则 ( )
( )A. | B.2 | C.4 | D.12 |
您最近一年使用:0次
23-24高三上·辽宁丹东·阶段练习
5 . 对任意的实数x, ,则
,则 值为( )
值为( )
 ,则
,则 值为( )
值为( )| A.60 | B.120 | C.240 | D.480 |
您最近一年使用:0次
23-24高三上·辽宁朝阳·阶段练习
名校
6 . 在二项式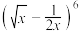 的展开式中,二项式系数最大的是( )
的展开式中,二项式系数最大的是( )
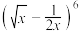 的展开式中,二项式系数最大的是( )
的展开式中,二项式系数最大的是( )| A.第3项 | B.第4项 |
| C.第5项 | D.第3项和第4项 |
您最近一年使用:0次
2014·山东青岛·一模
名校
7 .  展开式的常数项为
展开式的常数项为______ .
 展开式的常数项为
展开式的常数项为
您最近一年使用:0次
2023-11-30更新
|
2588次组卷
|
19卷引用:数学(北京卷01)
(已下线)数学(北京卷01)(已下线)解密22 排列组合与二项式定理 (讲义)-【高频考点解密】2021年高考数学(理)二轮复习讲义+分层训练北京市第十五中学2023届高三上学期12月月考数学试题北京市西城区第十五中学2024届高三上学期12月阶段测试数学试题北京市海淀区北京交大附中2024届高三下学期3月开学诊断练习数学试题(已下线)2014届山东省青岛市高三统一质量检测考试理科数学试卷2016届海南省文昌中学高三上学期期末考试理科数学试卷内蒙古包钢第一中学2015届高三适应性考试(一)数学(理)试题上海市杨浦高级中学2021届高三上学期9月月考数学试题山西省孝义市2021届高三下学期第九次模拟数学(理)试题河北省衡水第一中学2021届全国高三第二次联合考试(1)理科数学试题上海市2023届高三二模暨秋考模拟7数学试题上海市金山中学2023届高三核心素养检测数学试题新疆维吾尔自治区喀什地区巴楚县第一中学2022-2023学年高二下学期期中数学试题上海师范大学附属中学2024届高三上学期9月月考数学试题江苏省镇江市扬中高级中学2024届高三上学期十月学情检测数学试题新疆维吾尔自治区喀什地区喀什市2022-2023学年高二下学期期末质量监测数学试题(已下线)第六章 计数原理(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)江苏省南京市、盐城市2024届高三第一次模拟考试数学试题
23-24高三上·重庆·期中
名校
8 . 王老师每天早上7:00准时从家里出发去学校,他每天只会从地铁与汽车这两种交通工具之间选择一个乘坐.王老师多年积累的数据表明,他到达学校的时间在两种交通工具下的概率分布如下表所示:
(例如:表格中0.35的含义是如果王老师当天乘地铁去学校,则他到校时间在7:35-7:40的概率为0.35.)
(1)某天早上王老师通过抛一枚质地均匀的硬币决定乘坐地铁还是乘坐汽车去学校,若正面向上则坐地铁,反面向上则坐汽车.求他当天7:40-7:45到校的概率;
(2)已知今天(第一天)王老师选择乘坐地铁去学校,从第二天开始,若前一天到校时间早于7:40,则当天他会乘坐地铁去学校,否则当天他将乘坐汽车去学校.且若他连续10天乘坐地铁,则不论他前一天到校的时间是否早于7:40,第11天他都将坐汽车到校.记他从今天起(包括今天)到第一次乘坐汽车去学校前坐地铁的次数为 ,求
,求 ;
;
(3)已知今天(第一天)王老师选择乘坐地铁去学校.从第二天开始,若他前一天坐地铁去学校且到校时间早于7:40,则当天他会乘坐地铁去学校;若他前一天坐地铁去学校且到校时间晚于7:40,则当天他会乘坐汽车去学校;若他前一天乘坐汽车去学校,则不论他前一天到校的时间是否早于7:40,当天他都会乘坐地铁去学校.记 为王老师第
为王老师第 天坐地铁去学校的概率,求
天坐地铁去学校的概率,求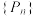 的通项公式.
的通项公式.
| 到校时间 | 7:30之前 | 7:30-7:35 | 7:35-7:40 | 7:40-7:45 | 7:45-7:50 | 7:50之后 |
| 乘地铁 | 0.1 | 0.15 | 0.35 | 0.2 | 0.15 | 0.05 |
| 乘汽车 | 0.25 | 0.3 | 0.2 | 0.1 | 0.1 | 0.05 |
(1)某天早上王老师通过抛一枚质地均匀的硬币决定乘坐地铁还是乘坐汽车去学校,若正面向上则坐地铁,反面向上则坐汽车.求他当天7:40-7:45到校的概率;
(2)已知今天(第一天)王老师选择乘坐地铁去学校,从第二天开始,若前一天到校时间早于7:40,则当天他会乘坐地铁去学校,否则当天他将乘坐汽车去学校.且若他连续10天乘坐地铁,则不论他前一天到校的时间是否早于7:40,第11天他都将坐汽车到校.记他从今天起(包括今天)到第一次乘坐汽车去学校前坐地铁的次数为
 ,求
,求 ;
;(3)已知今天(第一天)王老师选择乘坐地铁去学校.从第二天开始,若他前一天坐地铁去学校且到校时间早于7:40,则当天他会乘坐地铁去学校;若他前一天坐地铁去学校且到校时间晚于7:40,则当天他会乘坐汽车去学校;若他前一天乘坐汽车去学校,则不论他前一天到校的时间是否早于7:40,当天他都会乘坐地铁去学校.记
 为王老师第
为王老师第 天坐地铁去学校的概率,求
天坐地铁去学校的概率,求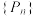 的通项公式.
的通项公式.
您最近一年使用:0次
2023-11-27更新
|
2037次组卷
|
8卷引用:黄金卷05
(已下线)黄金卷05(已下线)微考点7-2 递推方法计算概率与一维马尔科夫过程(数列与概率结合)(已下线)第七章 概率初步(续)(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)第29题 概率压轴大题(1)(高三二轮每日一题) 重庆市西南大学附属中学校2023-2024学年高三上学期期中考试数学试题2024届河北省承德市部分高中二模数学试题河北省衡水市部分学校2024届高三下学期二模考试数学试题江西省南昌市第十九中学2024届高三下学期第三次模拟考试数学试题
23-24高三上·江苏南京·期中
名校
解题方法
9 . 为弘扬中国共产党百年奋斗的光辉历程,某校团委决定举办“中国共产党党史知识”竞赛活动.竞赛共有 和
和 两类试题,每类试题各10题,其中每答对1道
两类试题,每类试题各10题,其中每答对1道 类试题得10分;每答对1道
类试题得10分;每答对1道 类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学
类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学 类试题中有7道题能答对,而他答对各道
类试题中有7道题能答对,而他答对各道 类试题的概率均为
类试题的概率均为 .
.
(1)若该同学只抽取3道 类试题作答,设
类试题作答,设 表示该同学答这3道试题的总得分,求
表示该同学答这3道试题的总得分,求 的分布和期望;
的分布和期望;
(2)若该同学在 类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
 和
和 两类试题,每类试题各10题,其中每答对1道
两类试题,每类试题各10题,其中每答对1道 类试题得10分;每答对1道
类试题得10分;每答对1道 类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学
类试题得20分,答错都不得分.每位参加竞赛的同学从这两类试题中共抽出3道题回答(每道题抽后不放回).已知某同学 类试题中有7道题能答对,而他答对各道
类试题中有7道题能答对,而他答对各道 类试题的概率均为
类试题的概率均为 .
.(1)若该同学只抽取3道
 类试题作答,设
类试题作答,设 表示该同学答这3道试题的总得分,求
表示该同学答这3道试题的总得分,求 的分布和期望;
的分布和期望;(2)若该同学在
 类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
类试题中只抽1道题作答,求他在这次竞赛中仅答对1道题的概率.
您最近一年使用:0次
2023-11-24更新
|
2850次组卷
|
9卷引用:黄金卷04
(已下线)黄金卷04(已下线)江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题变式题19-22江苏省南京市六校联合体2023-2024学年高三上学期11月期中数学试题江西省宜春市宜丰县宜丰中学2024届高三上学期12月月考数学试题河南省郑州市宇华实验学校2024届高三上学期12月月考数学试题(已下线)6.4.2超几何分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)福建省永春一中、培元中学、石光中学、季延中学2024届高三下学期第二次联合考试数学试题辽宁省大连市第八中学2023-2024学年高二下学期4月月考数学试题单元测试A卷——第七章 随机变量及其分布
23-24高二上·湖南常德·期中
名校
解题方法
10 . 甲、乙准备进行一局羽毛球比赛,比赛规定:一回合中赢球的一方作为下一回合的发球方.若甲发球,则本回合甲赢的概率为 ,若乙发球,则本回合甲赢的概率为
,若乙发球,则本回合甲赢的概率为 ,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
(1)求第3回合由乙发球的概率;
(2)求前3个回合中甲赢的回合数不低于乙的概率.
 ,若乙发球,则本回合甲赢的概率为
,若乙发球,则本回合甲赢的概率为 ,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.
,每回合比赛的结果相互独立.经抽签决定,第1回合由甲发球.(1)求第3回合由乙发球的概率;
(2)求前3个回合中甲赢的回合数不低于乙的概率.
您最近一年使用:0次
2023-11-11更新
|
570次组卷
|
4卷引用:黄金卷01






