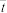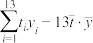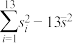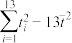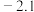1 . 用0,1,2,3,…,9十个数字可能组成多少个不同的
(1)三位数;
(2)无重复数字的三位数;
(3)小于500且没有重复数字的自然数?
(1)三位数;
(2)无重复数字的三位数;
(3)小于500且没有重复数字的自然数?
您最近一年使用:0次
2024-04-23更新
|
202次组卷
|
18卷引用:第01讲 分类加法计数原理与分步乘法计数原理 (高频考点,精讲)-2
(已下线)第01讲 分类加法计数原理与分步乘法计数原理 (高频考点,精讲)-2(已下线)分类加法计数原理和分步乘法计数原理(已下线)第六章 计数原理 讲核心 01(已下线)7.1 两个基本计数原理-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)(已下线)7.1两个基本计数原理-【帮课堂】2022-2023学年高二数学同步精品讲义(苏教版2019选择性必修第二册)(已下线)6.1 第2课时 分类加法计数原理与分步乘法计数原理的应用(练习)-2020-2021学年下学期高二数学同步精品课堂(新教材人教A版选择性必修第三册)人教A版(2019) 选修第三册 核心素养 第六章 6.1 分类加法计数原理与分步乘法计数原理广东省汕头市潮阳林百欣中学2021-2022学年高二下学期期中数学试题甘肃省天水市第一中学2021-2022学年高二下学期第一阶段考试数学(理)试题江苏省连云港市四校2021-2022学年高二下学期期中数学试题广西钦州市2022-2023学年高二上学期期末考试数学试题(已下线)3.1.1基本计数原理题组课堂练习-2022-2023学年高二下学期数学人教B版(2019)选择性必修第二册山东省枣庄市枣庄市第八中学2022-2023学年高二下学期3月月考数学试题浙江省宁波赫威斯肯特学校2022-2023学年高二普高部下学期第一次月考数学试题(已下线)专题14 两个基本计数原理3种常见考法归类-【寒假自学课】2024年高二数学寒假提升学与练(苏教版2019)(已下线)6.1 分类加法计数原理与分步乘法计数原理(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)山西省大同市浑源县第七中学校2023-2024学年高二下学期第一次月考数学试题(已下线)6.1分类加法计数原理与分步乘法计数原理——课堂例题
名校
解题方法
2 . 近年来,长安区大力发展大花卉产业,其中玫瑰既有观赏价值也能加工成食品和高档化妆品而得到环山路一带农民大面种植.已知玫瑰的株高y(单位:cm)与一定范围内的温度x(单位: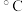 )有关,现收集了玫瑰的13组观测数据,得到如下的散点图:
)有关,现收集了玫瑰的13组观测数据,得到如下的散点图: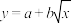 或
或 建立y关于x的回归方程,令
建立y关于x的回归方程,令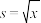 ,
,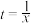 得到如下数据:
得到如下数据:
且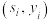 与
与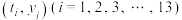 的相关系数分别为
的相关系数分别为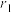 ,
,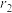 ,且
,且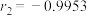 .
.
(1)用相关系数说明哪种模型建立y与x的回归方程更合适;
(2)根据(1)的结果及表中数据,建立y关于x的回归方程;
(3)已知玫瑰的利润z与x、y的关系为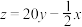 ,当x为何值时,z的预期最大.
,当x为何值时,z的预期最大.
参考数据和公式: ,
,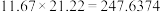 ,
,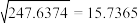 ,对于一组数据
,对于一组数据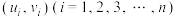 ,其回归直线方程
,其回归直线方程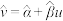 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为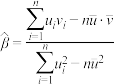 ,
, ,相关系数
,相关系数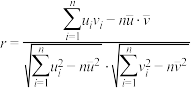 .
.
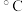 )有关,现收集了玫瑰的13组观测数据,得到如下的散点图:
)有关,现收集了玫瑰的13组观测数据,得到如下的散点图:
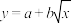 或
或 建立y关于x的回归方程,令
建立y关于x的回归方程,令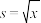 ,
,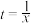 得到如下数据:
得到如下数据:
|
|
|
| ||||
10.15 | 109.94 | 3.04 | 0.16 | ||||
|
|
|
|
| |||
13.94 |
| 11.67 | 0.21 | 21.22 | |||
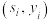 与
与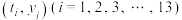 的相关系数分别为
的相关系数分别为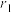 ,
,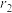 ,且
,且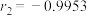 .
.(1)用相关系数说明哪种模型建立y与x的回归方程更合适;
(2)根据(1)的结果及表中数据,建立y关于x的回归方程;
(3)已知玫瑰的利润z与x、y的关系为
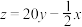 ,当x为何值时,z的预期最大.
,当x为何值时,z的预期最大.参考数据和公式:
 ,
,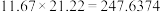 ,
,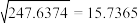 ,对于一组数据
,对于一组数据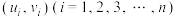 ,其回归直线方程
,其回归直线方程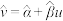 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为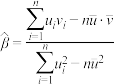 ,
, ,相关系数
,相关系数 .
.
您最近一年使用:0次
2024-04-10更新
|
1606次组卷
|
18卷引用:专题2.5 概率与统计-回归分析、独立性检验-2021年高考数学解答题挑战满分专项训练(新高考地区专用)
(已下线)专题2.5 概率与统计-回归分析、独立性检验-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题46 统计与统计案例-备战2022年高考数学一轮复习一网打尽之重点难点突破(已下线)第八章 成对数据的统计分析总结 第二课提炼本章思想(已下线)第八章 成对数据的统计分析总结 第三练 方法提升应用(已下线)重组1 高二期末真题重组卷(河北卷)B提升卷湖北省八市2021届高三下学期3月联考数学试题(已下线)专题8.1成对数据的统计相关性、一元线性回归模型及其应用(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)第八章 成对数据的统计分析单元测试B卷-【新高考题型】2020-2021学年高二数学下学期单元实战演练AB卷(人教A版2019)广东省深圳市宝安区2022届高三上学期第一次调研(10月)数学试题陕西省咸阳市武功县普集高中2021-2022学年高一宏志班下学期第一次月考数学试题广西河池市八校2021-2022学年高二下学期第一次联考数学(文)试题四川省宜宾天立学校2022-2023学年高二上学期第三学月考理科数学试题河北省石家庄市2022-2023学年高二下学期期末数学试题陕西省西安市长安区第一中学2023-2024学年高二下学期第一次教学质量检测数学试卷(已下线)模块四专题3重组综合练(陕西)(8+3+3+5模式)(北师大版高二)(已下线)模块一 专题1 《线性回归与相关性和独立性检验》(北师大版高二期中)B拔高卷(已下线)高二下学期第三次月考模拟卷(新题型)(范围:导数+选择性必修第三册)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)广东省东莞市东华高级中学、东华松山湖高级中学2022-2023学年高二下学期期末学习效率检测数学试题
名校
解题方法
3 . 2024年3月4日,丰城市农业局在市委组织下召开推进湖塘-董家富硒梨产业高质量发展专题会议,安排部署加快推进特色优势产业富硒梨高质量发展工作,集中资源、力量打造“富硒梨”公共品牌.丰城市为做好富硒梨产业的高质量发展,项目组统计了某果场近5年富硒梨产业综合总产值的各项数据如下:年份x,综合产值y(单位:万元)
(1)根据表格中的数据,可用一元线性回归模型刻画变量y与变量x之间的线性相关关系,请用相关系数加以说明(精确到0.01);
(2)求出y关于x的经验回归方程,并预测2024年底该果场富硒梨产业的综合总产值.
参考公式:相关系数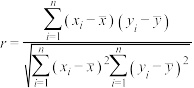 回归方程
回归方程 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: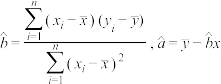 ;
;
参考数据:
| 年份 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
综合产值 | 23.1 | 37.0 | 62.1 | 111.6 | 150.8 |
(2)求出y关于x的经验回归方程,并预测2024年底该果场富硒梨产业的综合总产值.
参考公式:相关系数
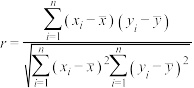 回归方程
回归方程 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: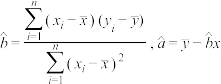 ;
;参考数据:

您最近一年使用:0次
2024-04-02更新
|
771次组卷
|
9卷引用:第三节 成对数据的统计分析(第一课时) B卷素养养成卷 一轮复习点点通
(已下线)第三节 成对数据的统计分析(第一课时) B卷素养养成卷 一轮复习点点通(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)贵州省天柱民族中学2024届高三上学期第三次月考数学试题新疆乌鲁木齐市第六十一中学2024届高三上学期第二次月考数学(文)试题(已下线)7.2成对数据的线性相关性(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)江西省丰城中学2023-2024学年高二下学期3月月考数学试题山东省潍坊市诸城繁华中学2023-2024学年高二下学期4月阶段检测数学试题单元测试B卷——第八章 成对数据的统计分析(已下线)模块三 专题1 大题分类练(线性回归)(北师大高二)
名校
解题方法
4 . 法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包.该面包店的面包师声称自己所出售的面包的平均质量是1 000 g,上下浮动不超过50 g.这句话用数学语言来表达就是:每个面包的质量服从期望为1 000 g,标准差为50 g的正态分布.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N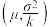 .利用该结论解决下面问题.
.利用该结论解决下面问题.
①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N
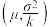 .利用该结论解决下面问题.
.利用该结论解决下面问题.①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
您最近一年使用:0次
2024-03-21更新
|
383次组卷
|
20卷引用:8.3 正态分布-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)
(已下线)8.3 正态分布-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)山东省青岛市四区2021-2022学年高三上学期期末考试数学试题福建省尤溪第一中学2021~2022学年高二下学期数学期末模拟卷(三)试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(五)数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题浙江省杭州第二中学2023届高三下学期3月月考数学试题江苏省常州市溧阳中学2022-2023学年高二下学期4月阶段性调研测试数学试题江苏省扬州中学2023届高三下学期阶段测试数学试题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题江苏省盐城市伍佑中学2023届高三高考热身考试数学试题辽宁省大连市第八中学2023届高考适应性测试数学试题福建省厦门第一中学2023届高三二模数学试题辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题
名校
解题方法
5 . 某校高一、高二、高三年级的学生人数之比为3:3:4,三个年级的学生都报名参加公益志愿活动,经过选拔,高一年级有 的学生成为公益活动志愿者,高二、高三年级各有
的学生成为公益活动志愿者,高二、高三年级各有 的学生成为公益活动志愿者.
的学生成为公益活动志愿者.
(1)设事件 “在三个年级中随机抽取的1名学生是志愿者”;事件
“在三个年级中随机抽取的1名学生是志愿者”;事件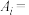 “在三个年级中随机抽取1名学生,该生来自高
“在三个年级中随机抽取1名学生,该生来自高 年级”(
年级”(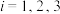 ).请完成下表中不同事件的概率并写出演算步骤:
).请完成下表中不同事件的概率并写出演算步骤:
(2)若在三个年级中随机抽取1名学生是志愿者,根据以上表中所得数据,求该学生来自于高一年级的概率.
 的学生成为公益活动志愿者,高二、高三年级各有
的学生成为公益活动志愿者,高二、高三年级各有 的学生成为公益活动志愿者.
的学生成为公益活动志愿者.(1)设事件
 “在三个年级中随机抽取的1名学生是志愿者”;事件
“在三个年级中随机抽取的1名学生是志愿者”;事件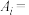 “在三个年级中随机抽取1名学生,该生来自高
“在三个年级中随机抽取1名学生,该生来自高 年级”(
年级”(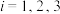 ).请完成下表中不同事件的概率并写出演算步骤:
).请完成下表中不同事件的概率并写出演算步骤:| 事件概率 | 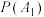 | 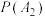 | 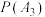 | 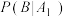 |  |  | 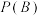 |
| 概率值 |  |
您最近一年使用:0次
2024-03-19更新
|
474次组卷
|
10卷引用:考点巩固卷24 古典概型、相互独立、条件概率及全概率公式(七大考点)
(已下线)考点巩固卷24 古典概型、相互独立、条件概率及全概率公式(七大考点)(已下线)考点11 条件概率与全概率公式 2024届高考数学考点总动员【练】(已下线)第02讲 7.1.2全概率公式-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)贵州省贵阳市2024届高三上学期8月摸底考试数学试题云南省红河州开远市第一中学校2023-2024学年高二下学期3月月考数学试题(已下线)8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)7.1.2 全概率公式——课后作业(提升版)河北省邯郸市永年区第二中学2023-2024学年高二下学期期中考试数学试卷
2023·全国·模拟预测
名校
解题方法
6 . 某公司为了解市场对其开发的新产品的需求情况,共调查了250名顾客,采取100分制对产品功能满意程度、产品外观满意程度分别进行评分,其中对产品功能满意程度的评分服从正态分布 ,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
(2)若这250人中对两项都非常满意的有2人,现从对产品功能非常满意和对产品外观非常满意的人中随机抽取3人,设3人中两项都非常满意的有X人,求X的分布列和数学期望. (附:若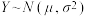 ,则
,则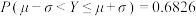 ,
, )
)
 ,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.
,对产品外观满意程度评分的频率分布直方图如图所示,规定评分90分以上(不含90分)视为非常满意.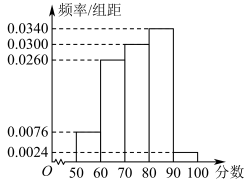
(2)若这250人中对两项都非常满意的有2人,现从对产品功能非常满意和对产品外观非常满意的人中随机抽取3人,设3人中两项都非常满意的有X人,求X的分布列和数学期望. (附:若
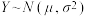 ,则
,则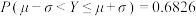 ,
, )
)
您最近一年使用:0次
2024-03-19更新
|
653次组卷
|
7卷引用:专题8-2分布列综合归类-2
(已下线)专题8-2分布列综合归类-2(已下线)第七章 随机变量及其分布总结 第一练 考点强化训练(已下线)2024年全国高考名校名师联席命制型数学信息卷(五)(已下线)2024年全国高考名校名师联席命制数学(理)信息卷(六)江西省上饶市玉山县第二中学2023-2024学年高二上学期12月月考数学试题江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(三)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
7 . 已知m,n是正整数,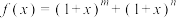 的展开式中x的系数为7.
的展开式中x的系数为7.
(1)求m,n为何值时, 的展开式中
的展开式中 的系数最小,并求出此时
的系数最小,并求出此时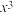 的系数;
的系数;
(2)利用(1)中结果,求 的近似值.(精确到0.01)
的近似值.(精确到0.01)
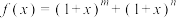 的展开式中x的系数为7.
的展开式中x的系数为7.(1)求m,n为何值时,
 的展开式中
的展开式中 的系数最小,并求出此时
的系数最小,并求出此时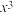 的系数;
的系数;(2)利用(1)中结果,求
 的近似值.(精确到0.01)
的近似值.(精确到0.01)
您最近一年使用:0次
2024-03-14更新
|
319次组卷
|
12卷引用:模块二专题3 《计数原理》单元检测篇 B提升卷(人教A)
(已下线)模块二专题3 《计数原理》单元检测篇 B提升卷(人教A)(已下线)模块二 专题1 《计数原理》单元检测篇 B提升卷(北师大2019版)(已下线)模块二 专题1 《计数原理》单元检测篇 B提升卷(人教B )(已下线)模块二 专题2 《计数原理》单元检测篇 B提升卷(苏教版)(已下线)考点08 二项式定理的应用 2024届高考数学考点总动员【练】(已下线)6.3.2 二项式系数的性质(6大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)2023版 北师大版(2019) 选修第一册 名师精选卷 第十三单元 二项式定理、杨辉三角第三章 排列、组合与二项式定理(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)(已下线)第六章 计数原理(章节单元检测)-【同步题型讲义】2022-2023学年高二数学同步教学题型讲义(人教A版2019选择性必修第三册)第五章 计数原理章末测评卷-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册 山东省烟台市爱华高级中学2023-2024学年高二下学期开学质量检测数学试题(已下线)6.3.2二项式系数的性质——课时作业(巩固版)
解题方法
8 . 乒乓球起源于英国的19世纪末,因为1959年的世界乒乓球锦标赛,中国参赛运动员为中国获得了第一个世界冠军,而使国人振奋,从此乒乓球运动在中国风靡,成为了事实上中国的国球的体育项目.国球在校园中的普及也丰富了老师、同学们的业余生活.某校拟从5名优秀乒乓球爱好者中抽选人员分批次参加社区共建活动.共建活动共分3批次进行,每次活动需要同时派送2名选手,且每次派送选手均从5人中随机抽选.已知这5名选手中,2人有比赛经验,3人没有比赛经验.
(1)求5名选手中的“1号选手”,在这3批次活动中有且只有一次被抽选到的概率;
(2)求第二次抽选时,选到没有比赛经验的选手的人数最有可能是几人?请说明理由;
(3)现在需要2名乒乓球选手完成某项特殊比赛任务,每次只能派一个人,且每个人只派一次,如果前一位选手不能赢得比赛,则再派另一位选手.若有A、 两位选手可派,他们各自完成任务的概率分别为
两位选手可派,他们各自完成任务的概率分别为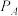 、
、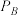 ,且
,且 ,各人能否完成任务相互独立.试分析以怎样的顺序派出选手,可使所需派出选手的人员数目的数学期望达到最小.
,各人能否完成任务相互独立.试分析以怎样的顺序派出选手,可使所需派出选手的人员数目的数学期望达到最小.
(1)求5名选手中的“1号选手”,在这3批次活动中有且只有一次被抽选到的概率;
(2)求第二次抽选时,选到没有比赛经验的选手的人数最有可能是几人?请说明理由;
(3)现在需要2名乒乓球选手完成某项特殊比赛任务,每次只能派一个人,且每个人只派一次,如果前一位选手不能赢得比赛,则再派另一位选手.若有A、
 两位选手可派,他们各自完成任务的概率分别为
两位选手可派,他们各自完成任务的概率分别为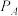 、
、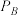 ,且
,且 ,各人能否完成任务相互独立.试分析以怎样的顺序派出选手,可使所需派出选手的人员数目的数学期望达到最小.
,各人能否完成任务相互独立.试分析以怎样的顺序派出选手,可使所需派出选手的人员数目的数学期望达到最小.
您最近一年使用:0次
解题方法
9 . 直播带货是一种直播和电商相结合的销售手段,目前已被广大消费者所接受.针对这种现状,某公司决定逐月加大直播带货的投入,直播带货金额稳步提升,以下是该公司2023年前5个月的带货金额的统计表(金额 (万元)).
(万元)).
(1)根据统计表,
①求该公司带货金额的平均值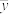 ;
;
②求该公司带货金额 与月份编号
与月份编号 的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(
的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(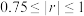 ,则认为
,则认为 与
与 的线性相关性较强;
的线性相关性较强;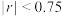 ,则认为
,则认为 与
与 的线性相关性较弱);
的线性相关性较弱);
(2)该公司现有一个直播间销售甲、乙两种产品.为对产品质量进行监控,质检人员先用简单随机抽样的方法从甲、乙两种产品中分别抽取了5件、3件产品进行初检,再从中随机选取3件做进一步的质检,记抽到甲产品的件数为 ,试求
,试求 的分布列与期望.
的分布列与期望.
附:相关系数公式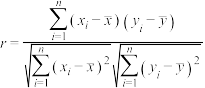 ,参考数据:
,参考数据: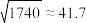 ,
,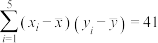 ,
, ,
, .
.
 (万元)).
(万元)).| 月份 | 1月 | 2月 | 3月 | 4月 | 5月 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
金额 (万元) (万元) | 7 | 12 | 13 | 19 | 24 |
①求该公司带货金额的平均值
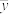 ;
;②求该公司带货金额
 与月份编号
与月份编号 的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(
的样本相关系数(精确到0.01),并判断它们是否具有线性相关关系(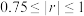 ,则认为
,则认为 与
与 的线性相关性较强;
的线性相关性较强;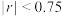 ,则认为
,则认为 与
与 的线性相关性较弱);
的线性相关性较弱);(2)该公司现有一个直播间销售甲、乙两种产品.为对产品质量进行监控,质检人员先用简单随机抽样的方法从甲、乙两种产品中分别抽取了5件、3件产品进行初检,再从中随机选取3件做进一步的质检,记抽到甲产品的件数为
 ,试求
,试求 的分布列与期望.
的分布列与期望.附:相关系数公式
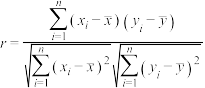 ,参考数据:
,参考数据: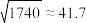 ,
,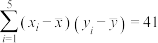 ,
, ,
, .
.
您最近一年使用:0次
2024-03-08更新
|
865次组卷
|
6卷引用:专题8.1 成对数据的统计相关性【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
(已下线)专题8.1 成对数据的统计相关性【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)8.1.1变量的相关关系+8.1.2样本相关系数 第三课 知识扩展延伸(已下线)专题8.6 成对数据的统计分析全章八大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)内蒙古赤峰市2024届高三上学期1.30模拟理科数学试题(已下线)8.1 成对数据的统计相关性——课后作业(提升版)
10 . 某工厂有工人200名,统计他们某天加工产品的件数,统计数据如下表所示:
规定一天加工产品件数大于70的工人为“生产标兵”.已知这天的生产标兵中年龄大于30岁的有15人,这15人占该工厂年龄大于30岁的工人数的 .
.
(1)完成下面的 列联表,根据小概率值
列联表,根据小概率值 的独立性检验,能否认为该工厂的工人是否为生产标兵与年龄有关?
的独立性检验,能否认为该工厂的工人是否为生产标兵与年龄有关?
(2)该工厂采用“阶梯式”的计件工资:日加工产品不超过50件的部分每件1元,超过50件但不超过60件的部分每件2元,超过60件但不超过80件的部分每件3元,超过80件的部分每件5元.假设工人小张每天加工产品的件数只可能为样本数据中各分组区间的右端点值,用对应区间的频率估计其概率,求小张每天的计件工资 (单位:元)的期望.
(单位:元)的期望.
附: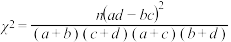 .
.
| 加工产品的件数 | 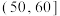 |  |  |  |  |
| 人数 | 50 | 80 | 40 | 20 | 10 |
 .
.(1)完成下面的
 列联表,根据小概率值
列联表,根据小概率值 的独立性检验,能否认为该工厂的工人是否为生产标兵与年龄有关?
的独立性检验,能否认为该工厂的工人是否为生产标兵与年龄有关?| 年龄不大于30岁 | 年龄大于30岁 | |
| 生产标兵 | ||
| 非生产标兵 |
(2)该工厂采用“阶梯式”的计件工资:日加工产品不超过50件的部分每件1元,超过50件但不超过60件的部分每件2元,超过60件但不超过80件的部分每件3元,超过80件的部分每件5元.假设工人小张每天加工产品的件数只可能为样本数据中各分组区间的右端点值,用对应区间的频率估计其概率,求小张每天的计件工资
 (单位:元)的期望.
(单位:元)的期望.附:
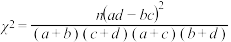 .
. | 0.05 | 0.01 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次