1 . 已知函数 .
.
(1)当 时,讨论函数
时,讨论函数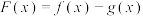 的单调性;
的单调性;
(2)当 时,求曲线
时,求曲线 与
与 的公切线方程.
的公切线方程.
 .
.(1)当
 时,讨论函数
时,讨论函数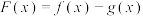 的单调性;
的单调性;(2)当
 时,求曲线
时,求曲线 与
与 的公切线方程.
的公切线方程.
您最近一年使用:0次
2023-04-10更新
|
833次组卷
|
3卷引用:重庆市第八中学2024届高三上学期入学测试数学试题
名校
解题方法
2 . 在 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且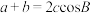 .
.
(1)求证: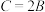 ;
;
(2)求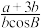 的最小值.
的最小值.
 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且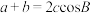 .
.(1)求证:
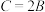 ;
;(2)求
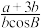 的最小值.
的最小值.
您最近一年使用:0次
2023-04-10更新
|
4866次组卷
|
9卷引用:重庆市第八中学校2023-2024学年高二上学期开学适应性训练数学试题
重庆市第八中学校2023-2024学年高二上学期开学适应性训练数学试题重庆市万州第二高级中学2023届高三三诊数学试题江西省宜春市2023届高三一模数学(文)试题江西省宜春市2023届高三一模数学(理)试题(已下线)专题06三角函数与解三角形(解答题)(已下线)高一数学下学期第二次月考02(范围:平面向量,解三角形,复数,立体几何)云南省玉溪第一中学2022-2023学年高一下学期期中考试数学试题湖北省武汉市第六中学2022-2023学年高一下学期第六次月考数学试题广东省茂名市第一中学2023届高三下学期5月第三次半月考数学试题
名校
3 .  、
、 、
、 、
、 、
、 五个队进行单循环赛(单循环赛制是指所有参赛队在竞赛中均能相遇一次),胜一场得3分,负一场得0分,平局各得1分.若
五个队进行单循环赛(单循环赛制是指所有参赛队在竞赛中均能相遇一次),胜一场得3分,负一场得0分,平局各得1分.若 队2胜2负,
队2胜2负, 队得8分,
队得8分, 队得9分,
队得9分, 队胜了
队胜了 队,则
队,则 队得分为
队得分为___________ .
 、
、 、
、 、
、 、
、 五个队进行单循环赛(单循环赛制是指所有参赛队在竞赛中均能相遇一次),胜一场得3分,负一场得0分,平局各得1分.若
五个队进行单循环赛(单循环赛制是指所有参赛队在竞赛中均能相遇一次),胜一场得3分,负一场得0分,平局各得1分.若 队2胜2负,
队2胜2负, 队得8分,
队得8分, 队得9分,
队得9分, 队胜了
队胜了 队,则
队,则 队得分为
队得分为
您最近一年使用:0次
2023-04-07更新
|
1675次组卷
|
3卷引用:重庆市南开中学校2023-2024学年高一上学期开学考试数学试题
名校
解题方法
4 . 我国南北朝时期的数学家祖冲之(公元429年-500年)计算出圆周率的精确度记录在世界保持了千年之久,德国数学家鲁道夫(公元1540年-1610年)用一生精力计算出了圆周率的35位小数,随着科技的进步,一些常数的精确度不断被刷新.例如:我们很容易能利用计算器得出函数 的零点
的零点 的近似值,为了实际应用,本题中取
的近似值,为了实际应用,本题中取 的值为-0.57.哈三中毕业生创办的仓储型物流公司建造了占地面积足够大的仓库,内部建造了一条智能运货总干线
的值为-0.57.哈三中毕业生创办的仓储型物流公司建造了占地面积足够大的仓库,内部建造了一条智能运货总干线 ,其在已经建立的直角坐标系中的函数解析式为
,其在已经建立的直角坐标系中的函数解析式为 ,其在
,其在 处的切线为
处的切线为 ,现计划再建一条总干线
,现计划再建一条总干线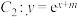 ,其中m为待定的常数.
,其中m为待定的常数.
注明:本题中计算的最终结果均用数字表示.
(1)求出 的直线方程,并且证明:在直角坐标系中,智能运货总干线
的直线方程,并且证明:在直角坐标系中,智能运货总干线 上的点不在直线
上的点不在直线 的上方;
的上方;
(2)在直角坐标系中,设直线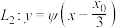 ,计划将仓库中直线
,计划将仓库中直线 与
与 之间的部分设为隔离区,两条运货总干线
之间的部分设为隔离区,两条运货总干线 、
、 分别在各自的区域内,即曲线
分别在各自的区域内,即曲线 上的点不能越过直线
上的点不能越过直线 ,求实数m的取值范围.
,求实数m的取值范围.
 的零点
的零点 的近似值,为了实际应用,本题中取
的近似值,为了实际应用,本题中取 的值为-0.57.哈三中毕业生创办的仓储型物流公司建造了占地面积足够大的仓库,内部建造了一条智能运货总干线
的值为-0.57.哈三中毕业生创办的仓储型物流公司建造了占地面积足够大的仓库,内部建造了一条智能运货总干线 ,其在已经建立的直角坐标系中的函数解析式为
,其在已经建立的直角坐标系中的函数解析式为 ,其在
,其在 处的切线为
处的切线为 ,现计划再建一条总干线
,现计划再建一条总干线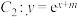 ,其中m为待定的常数.
,其中m为待定的常数.注明:本题中计算的最终结果均用数字表示.
(1)求出
 的直线方程,并且证明:在直角坐标系中,智能运货总干线
的直线方程,并且证明:在直角坐标系中,智能运货总干线 上的点不在直线
上的点不在直线 的上方;
的上方;(2)在直角坐标系中,设直线
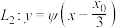 ,计划将仓库中直线
,计划将仓库中直线 与
与 之间的部分设为隔离区,两条运货总干线
之间的部分设为隔离区,两条运货总干线 、
、 分别在各自的区域内,即曲线
分别在各自的区域内,即曲线 上的点不能越过直线
上的点不能越过直线 ,求实数m的取值范围.
,求实数m的取值范围.
您最近一年使用:0次
2023-03-30更新
|
1365次组卷
|
6卷引用:重庆市乌江新高考协作体2024届高三下学期开学数学试题
名校
解题方法
5 . 已知函数 的定义域为
的定义域为 ,若函数
,若函数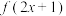 为奇函数,且
为奇函数,且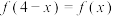 ,
,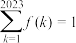 ,则
,则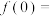 ( )
( )
A. | B.0 | C.1 | D.2 |
您最近一年使用:0次
2023-03-28更新
|
2230次组卷
|
8卷引用:重庆市西北狼教育联盟2024届高三上学期开学考试数学试题
重庆市西北狼教育联盟2024届高三上学期开学考试数学试题湖南省常德市2023届高三下学期一模数学试题专题03函数的概念与基本初等函数(已下线)押新高考第8题 函数的基本性质宁夏银川一中2022-2023学年高二下学期期中考试数学(文)试题(已下线)山东省实验中学2024届高三第一次诊断考试数学试题变式题6-10(已下线)专题20 函数的基本性质小题(单调性、奇偶性、周期性、对称性)(已下线)第三章 函数及其应用3.4 函数的对称性与周期性
名校
解题方法
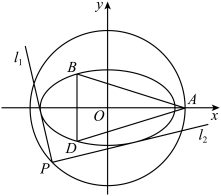
6 . 法国数学家加斯帕尔·蒙日是19世纪著名的几何学家,他创立了画法几何学,推动了空间解析几何学的独立发展,奠定了空间微分几何学的宽厚基础,根据他的研究成果,我们定义:给定椭圆 :
: ,则称圆心在原点
,则称圆心在原点 ,半径是
,半径是 的圆为“椭圆
的圆为“椭圆 的伴随圆”,已知椭圆
的伴随圆”,已知椭圆 的一个焦点为
的一个焦点为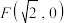 ,其短轴的一个端点到焦点
,其短轴的一个端点到焦点 的距离为
的距离为 .
. 为椭圆
为椭圆 的“伴随圆”与
的“伴随圆”与 轴正半轴的交点,
轴正半轴的交点, ,
, 是椭圆
是椭圆 的两相异点,且
的两相异点,且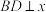 轴,求
轴,求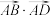 的取值范围.
的取值范围.
(2)在椭圆 的“伴随圆”上任取一点
的“伴随圆”上任取一点 ,过点
,过点 作直线
作直线 ,
, ,使得
,使得 ,
, 与椭圆
与椭圆 都只有一个交点,试判断
都只有一个交点,试判断 ,
, 是否垂直?并说明理由.
是否垂直?并说明理由.
 :
: ,则称圆心在原点
,则称圆心在原点 ,半径是
,半径是 的圆为“椭圆
的圆为“椭圆 的伴随圆”,已知椭圆
的伴随圆”,已知椭圆 的一个焦点为
的一个焦点为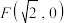 ,其短轴的一个端点到焦点
,其短轴的一个端点到焦点 的距离为
的距离为 .
.
 为椭圆
为椭圆 的“伴随圆”与
的“伴随圆”与 轴正半轴的交点,
轴正半轴的交点, ,
, 是椭圆
是椭圆 的两相异点,且
的两相异点,且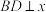 轴,求
轴,求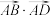 的取值范围.
的取值范围.(2)在椭圆
 的“伴随圆”上任取一点
的“伴随圆”上任取一点 ,过点
,过点 作直线
作直线 ,
, ,使得
,使得 ,
, 与椭圆
与椭圆 都只有一个交点,试判断
都只有一个交点,试判断 ,
, 是否垂直?并说明理由.
是否垂直?并说明理由.
您最近一年使用:0次
2023-03-25更新
|
819次组卷
|
5卷引用:重庆市乌江新高考协作体2023-2024学年高二下学期开学学业质量联合调研抽测数学试题
重庆市乌江新高考协作体2023-2024学年高二下学期开学学业质量联合调研抽测数学试题内蒙古赤峰市八校2023届高三第三次统一模拟考试联考文科数学试题(已下线)第五篇 向量与几何 专题1 蒙日圆与阿氏圆 微点9 阿波罗尼斯圆综合训练2024届广东省高三毕业班综合能力测试(华娇教育摸底测试)数学试题 广东省普宁二中实验学校2023-2024学年高二下学期第一次月考数学试题
名校
7 . 已知函数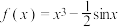 ,若
,若 ,
,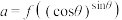 ,
,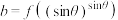 ,
,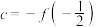 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )
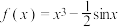 ,若
,若 ,
,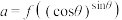 ,
,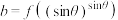 ,
,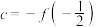 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( )A.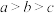 | B.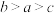 | C.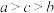 | D.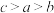 |
您最近一年使用:0次
2023-03-24更新
|
2556次组卷
|
8卷引用:重庆市乌江新高考协作体2024届高三下学期开学数学试题
重庆市乌江新高考协作体2024届高三下学期开学数学试题山东省青岛市2023届高三下学期第一次适应性检测数学试题专题05导数及其应用(选择题)(已下线)模块八 专题4 以导数为背景的压轴小题(已下线)押新高考第8题 函数的基本性质(已下线)“8+4+4”小题强化训练(24)(已下线)重难点突破01 玩转指对幂比较大小(十大题型)(已下线)专题23 导数及其应用小题
名校
8 . 已知 为抛物线
为抛物线 的焦点,A、B、C为抛物线上三点,当
的焦点,A、B、C为抛物线上三点,当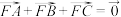 时,则在点A、B、C中横坐标大于2的有( )
时,则在点A、B、C中横坐标大于2的有( )
 为抛物线
为抛物线 的焦点,A、B、C为抛物线上三点,当
的焦点,A、B、C为抛物线上三点,当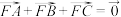 时,则在点A、B、C中横坐标大于2的有( )
时,则在点A、B、C中横坐标大于2的有( )| A.3个 | B.2个 | C.1 | D.0个 |
您最近一年使用:0次
2023-03-06更新
|
759次组卷
|
4卷引用:重庆市第一中学校2023-2024学年高二下学期开学考试数学试题
重庆市第一中学校2023-2024学年高二下学期开学考试数学试题上海市川沙中学2023届高三上学期期末数学试题(已下线)模拟检测卷03(文科)(已下线)专题04 圆锥曲线(六大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)
9 . 已知椭圆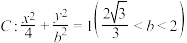 ,动圆
,动圆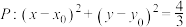 (圆心
(圆心 为椭圆
为椭圆 上异于左右顶点的任意一点),过原点
上异于左右顶点的任意一点),过原点 作两条射线与圆
作两条射线与圆 相切,分别交椭圆于
相切,分别交椭圆于 两点,且切线长的最小值为
两点,且切线长的最小值为 .
.
(1)求椭圆 的方程;
的方程;
(2)(i)若 、
、 斜率都存在,记为
斜率都存在,记为 ,
, (
( ),求
),求 的值.
的值.
(ii)求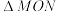 的面积.
的面积.
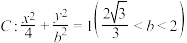 ,动圆
,动圆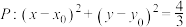 (圆心
(圆心 为椭圆
为椭圆 上异于左右顶点的任意一点),过原点
上异于左右顶点的任意一点),过原点 作两条射线与圆
作两条射线与圆 相切,分别交椭圆于
相切,分别交椭圆于 两点,且切线长的最小值为
两点,且切线长的最小值为 .
.(1)求椭圆
 的方程;
的方程;(2)(i)若
 、
、 斜率都存在,记为
斜率都存在,记为 ,
, (
( ),求
),求 的值.
的值.(ii)求
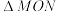 的面积.
的面积.
您最近一年使用:0次
名校
解题方法
10 . 已知关于 的不等式
的不等式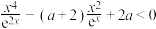 恰有两个正整数解,则实数
恰有两个正整数解,则实数 的取值范围是
的取值范围是______ .
 的不等式
的不等式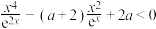 恰有两个正整数解,则实数
恰有两个正整数解,则实数 的取值范围是
的取值范围是
您最近一年使用:0次



