名校
解题方法
1 . 已知实数 满足
满足 ,则
,则 的最大值为
的最大值为______ ; 的取值范围为
的取值范围为______ .
 满足
满足 ,则
,则 的最大值为
的最大值为 的取值范围为
的取值范围为
您最近一年使用:0次
名校
解题方法
2 . 设双曲线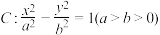 的左、右焦点分别为
的左、右焦点分别为 ,过坐标原点的直线与
,过坐标原点的直线与 交于
交于 点,
点,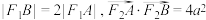 ,则
,则 的离心率为
的离心率为____________ .
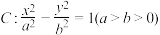 的左、右焦点分别为
的左、右焦点分别为 ,过坐标原点的直线与
,过坐标原点的直线与 交于
交于 点,
点,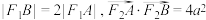 ,则
,则 的离心率为
的离心率为
您最近一年使用:0次
2024-02-29更新
|
604次组卷
|
5卷引用:重庆市铜梁中学校2023-2024学年高二下学期开学考试数学试题
重庆市铜梁中学校2023-2024学年高二下学期开学考试数学试题吉林省四校2023-2024学年高二下学期期初联考数学试题(已下线)专题15 双曲线离心率(一题多解)河北省石家庄精英中学2023-2024学年高二上学期期末数学试题(已下线)第1题 双曲线的离心率问题(5月)(压轴小题)
3 . 已知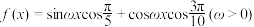 ,若
,若 在
在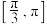 内恰有两个零点,则
内恰有两个零点,则 的取值范围是
的取值范围是______ .
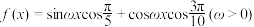 ,若
,若 在
在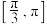 内恰有两个零点,则
内恰有两个零点,则 的取值范围是
的取值范围是
您最近一年使用:0次
4 . 已知函数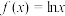 ,
,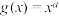 (
( ,
, ),若存在直线l,使得l是曲线
),若存在直线l,使得l是曲线 与曲线
与曲线 的公切线,则实数a的取值范围是
的公切线,则实数a的取值范围是__________ .
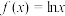 ,
,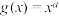 (
( ,
, ),若存在直线l,使得l是曲线
),若存在直线l,使得l是曲线 与曲线
与曲线 的公切线,则实数a的取值范围是
的公切线,则实数a的取值范围是
您最近一年使用:0次
名校
5 . 已知定义在 上的偶函数
上的偶函数 满足
满足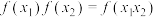 ,且当
,且当 时,
时, .若
.若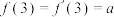 ,则
,则 在点
在点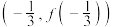 处的切线方程为
处的切线方程为______ .(结果用含 的表达式表示)
的表达式表示)
 上的偶函数
上的偶函数 满足
满足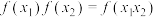 ,且当
,且当 时,
时, .若
.若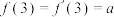 ,则
,则 在点
在点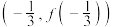 处的切线方程为
处的切线方程为 的表达式表示)
的表达式表示)
您最近一年使用:0次
2024-02-20更新
|
1688次组卷
|
2卷引用:重庆市第八中学校2023-2024学年高三下学期入学适应性考试数学试题
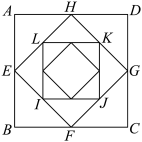
6 . 如图,正方形 的边长为1,连接
的边长为1,连接 各边的中点得到正方形
各边的中点得到正方形 ,连接正方形
,连接正方形 各边的中点得到正方形
各边的中点得到正方形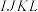 ,依此方法一直进行下去.记
,依此方法一直进行下去.记 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形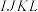 的面积,……..
的面积,……..  为
为 的前
的前 项和.给出下列四个结论:
项和.给出下列四个结论:
①存在常数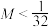 ,使得
,使得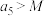 恒成立;②存在正整数
恒成立;②存在正整数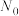 ,当
,当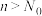 时,
时,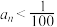 ;③存在常数
;③存在常数 ,使得
,使得 恒成立;④存在正整数
恒成立;④存在正整数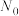 ,当
,当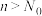 时,
时, 其中所有正确结论的序号是
其中所有正确结论的序号是_________ .
 的边长为1,连接
的边长为1,连接 各边的中点得到正方形
各边的中点得到正方形 ,连接正方形
,连接正方形 各边的中点得到正方形
各边的中点得到正方形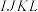 ,依此方法一直进行下去.记
,依此方法一直进行下去.记 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形 的面积,
的面积, 为正方形
为正方形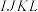 的面积,……..
的面积,……..  为
为 的前
的前 项和.给出下列四个结论:
项和.给出下列四个结论:
①存在常数
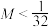 ,使得
,使得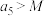 恒成立;②存在正整数
恒成立;②存在正整数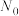 ,当
,当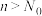 时,
时,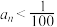 ;③存在常数
;③存在常数 ,使得
,使得 恒成立;④存在正整数
恒成立;④存在正整数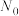 ,当
,当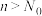 时,
时, 其中所有正确结论的序号是
其中所有正确结论的序号是
您最近一年使用:0次
2024-01-19更新
|
339次组卷
|
3卷引用:重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题
重庆市万州二中教育集团2023-2024学年高二下学期入学质量监测数学试题北京市东城区2023-2024学年高二上学期期末统一检测数学试卷(已下线)第4章 数列 单元综合检测(难点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
名校
解题方法
7 . 若定义在 上的函数
上的函数 满足
满足 ,且当
,且当 时,
时, ,则
,则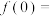
________________ ,若 ,则满足不等式
,则满足不等式 的
的 的取值范围是
的取值范围是_______________ .
 上的函数
上的函数 满足
满足 ,且当
,且当 时,
时, ,则
,则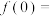
 ,则满足不等式
,则满足不等式 的
的 的取值范围是
的取值范围是
您最近一年使用:0次
2024-01-11更新
|
461次组卷
|
3卷引用:重庆市九龙坡区育才中学2023-2024学年高一下学期寒假检测定时训练数学试题
重庆市九龙坡区育才中学2023-2024学年高一下学期寒假检测定时训练数学试题重庆市北碚区2023-2024学年高一上学期期末学业水平阶段质量调研抽测数学试题(已下线)专题05 三角函数4-2024年高一数学寒假作业单元合订本
名校
解题方法
8 . 如图,已知椭圆 ,其焦距为4,过椭圆长轴上一动点
,其焦距为4,过椭圆长轴上一动点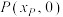 作直线交椭圆于
作直线交椭圆于 、
、 ,直线
,直线 、
、 交于点
交于点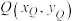 ,已知
,已知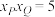 ,则椭圆的离心率为
,则椭圆的离心率为______ .

 ,其焦距为4,过椭圆长轴上一动点
,其焦距为4,过椭圆长轴上一动点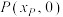 作直线交椭圆于
作直线交椭圆于 、
、 ,直线
,直线 、
、 交于点
交于点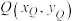 ,已知
,已知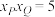 ,则椭圆的离心率为
,则椭圆的离心率为
您最近一年使用:0次
2024-01-11更新
|
382次组卷
|
2卷引用:重庆市乌江新高考协作体2023-2024学年高二下学期开学学业质量联合调研抽测数学试题
名校
9 . 已知有限集合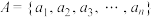 ,定义集合
,定义集合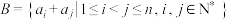 中的元素个数为集合
中的元素个数为集合 的“容量”,记为
的“容量”,记为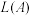 .若集合
.若集合 ,则
,则
__________ ;若集合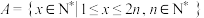 ,且
,且 ,则正整数
,则正整数 的值是
的值是__________ .
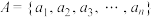 ,定义集合
,定义集合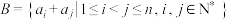 中的元素个数为集合
中的元素个数为集合 的“容量”,记为
的“容量”,记为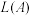 .若集合
.若集合 ,则
,则
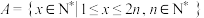 ,且
,且 ,则正整数
,则正整数 的值是
的值是
您最近一年使用:0次
2023-09-19更新
|
733次组卷
|
4卷引用:重庆市南开中学校2023-2024学年高一上学期开学考试数学试题
名校
解题方法
10 . 定义在 上的偶函数
上的偶函数 满足
满足 ,且当
,且当 时,
时,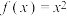 ,函数
,函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,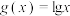 ,则函数
,则函数 的零点的个数是
的零点的个数是________ .
 上的偶函数
上的偶函数 满足
满足 ,且当
,且当 时,
时,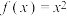 ,函数
,函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,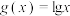 ,则函数
,则函数 的零点的个数是
的零点的个数是
您最近一年使用:0次
2023-09-03更新
|
588次组卷
|
2卷引用:重庆市七校2024届高三上学期开学考试数学试题



