解题方法
1 . 已知函数 ,函数
,函数 的单调递减区间为
的单调递减区间为 ,且函数
,且函数 的极小值为0.
的极小值为0.
(1)求函数 的解析式;
的解析式;
(2)证明: .
.
 ,函数
,函数 的单调递减区间为
的单调递减区间为 ,且函数
,且函数 的极小值为0.
的极小值为0.(1)求函数
 的解析式;
的解析式;(2)证明:
 .
.
您最近一年使用:0次
解题方法
2 . 已知函数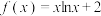 ,
,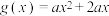 .
.
(1)当 时,求证:
时,求证: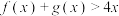 ;
;
(2)若 是函数
是函数 的导函数,且
的导函数,且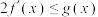 在定义域
在定义域 内恒成立,求整数a的最小值.
内恒成立,求整数a的最小值.
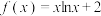 ,
,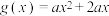 .
.(1)当
 时,求证:
时,求证: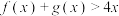 ;
;(2)若
 是函数
是函数 的导函数,且
的导函数,且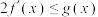 在定义域
在定义域 内恒成立,求整数a的最小值.
内恒成立,求整数a的最小值.
您最近一年使用:0次
3 . 在平面直角坐标系xOy中,已知抛物线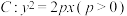 的焦点为F,过F的直线l与该抛物线交于A,B两点,过焦点F且垂直于直线l的直线
的焦点为F,过F的直线l与该抛物线交于A,B两点,过焦点F且垂直于直线l的直线 与抛物线C的准线交于点P.当直线l的斜率为1时,
与抛物线C的准线交于点P.当直线l的斜率为1时,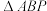 的面积为
的面积为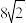 .
.
(1)求抛物线C的方程;
(2)求 的取值范围.
的取值范围.
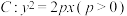 的焦点为F,过F的直线l与该抛物线交于A,B两点,过焦点F且垂直于直线l的直线
的焦点为F,过F的直线l与该抛物线交于A,B两点,过焦点F且垂直于直线l的直线 与抛物线C的准线交于点P.当直线l的斜率为1时,
与抛物线C的准线交于点P.当直线l的斜率为1时,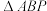 的面积为
的面积为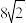 .
.(1)求抛物线C的方程;
(2)求
 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-11更新
|
466次组卷
|
3卷引用:贵州省黔东南自治州镇远县文德民族中学校2022届高三上学期期末数学(理)试题
解题方法
4 . 已知函数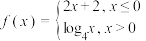 ,则函数
,则函数 的所有零点之和为
的所有零点之和为___________ .
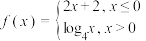 ,则函数
,则函数 的所有零点之和为
的所有零点之和为
您最近一年使用:0次
5 . 双曲线C: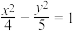 的左、右焦点分别为
的左、右焦点分别为 ,过点
,过点 的直线与双曲线右支交于A、B两点,
的直线与双曲线右支交于A、B两点,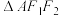 和
和 内切圆半径分别为
内切圆半径分别为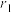 和
和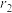 ,则( )
,则( )
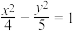 的左、右焦点分别为
的左、右焦点分别为 ,过点
,过点 的直线与双曲线右支交于A、B两点,
的直线与双曲线右支交于A、B两点,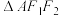 和
和 内切圆半径分别为
内切圆半径分别为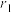 和
和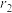 ,则( )
,则( )A.双曲线C的渐近线方程为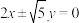 |
B.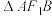 面积的最小值为15 面积的最小值为15 |
C.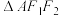 和 和 的内切圆圆心的连线与x轴垂直 的内切圆圆心的连线与x轴垂直 |
D. 为定值 为定值 |
您最近一年使用:0次
2023-02-19更新
|
518次组卷
|
2卷引用:贵州省遵义市2022-2023学年高二上学期期末数学试题
6 . 已知椭圆 的离心率为
的离心率为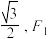 、
、 分别为椭圆
分别为椭圆 的左、右焦点,
的左、右焦点, 为椭圆
为椭圆 上一点,
上一点,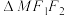 的周长为
的周长为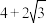 .
.
(1)求椭圆 的方程;
的方程;
(2)若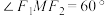 ,求
,求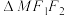 的面积;
的面积;
(3)设 为圆
为圆 上任意一点,过
上任意一点,过 作椭圆
作椭圆 的两条切线,切点分别为
的两条切线,切点分别为 ,判断
,判断 是否为定值?若是,求出定值;若不是,说明理由.
是否为定值?若是,求出定值;若不是,说明理由.
 的离心率为
的离心率为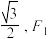 、
、 分别为椭圆
分别为椭圆 的左、右焦点,
的左、右焦点, 为椭圆
为椭圆 上一点,
上一点,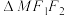 的周长为
的周长为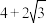 .
.(1)求椭圆
 的方程;
的方程;(2)若
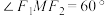 ,求
,求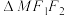 的面积;
的面积;(3)设
 为圆
为圆 上任意一点,过
上任意一点,过 作椭圆
作椭圆 的两条切线,切点分别为
的两条切线,切点分别为 ,判断
,判断 是否为定值?若是,求出定值;若不是,说明理由.
是否为定值?若是,求出定值;若不是,说明理由.
您最近一年使用:0次
2022-11-29更新
|
703次组卷
|
4卷引用:选择性必修第一册综合测试卷-2022-2023学年高二上学期数学人教B版(2019)
名校
解题方法
7 . 抛物线 的焦点为
的焦点为 ,其准线与
,其准线与 轴的交点为
轴的交点为 ,过点
,过点 作直线与此抛物线交于
作直线与此抛物线交于 ,
, 两点,若
两点,若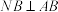 ,则
,则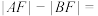 ( )
( )
 的焦点为
的焦点为 ,其准线与
,其准线与 轴的交点为
轴的交点为 ,过点
,过点 作直线与此抛物线交于
作直线与此抛物线交于 ,
, 两点,若
两点,若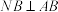 ,则
,则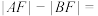 ( )
( )| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
2022-08-13更新
|
1499次组卷
|
7卷引用:贵州省贵阳市白云区第二高级中学2021-2022学年高二下学期期末联考数学(理)试题
贵州省贵阳市白云区第二高级中学2021-2022学年高二下学期期末联考数学(理)试题贵州省贵阳市白云区第二高级中学2021-2022学年高二下学期期末联考数学(文)试题(已下线)第三章 圆锥曲线的方程(A卷·知识通关练)(5)(已下线)第03讲 抛物线(练)(已下线)专题9-4 抛物线性质应用归类-2江西省乐平中学2022-2023学年高二下学期3月月考数学试题(已下线)高二上学期期中考试选择题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)
解题方法
8 . 已知抛物线的顶点为坐标原点,焦点在坐标轴上,设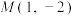 是抛物线上一点.
是抛物线上一点.
(1)求抛物线方程;
(2)若抛物线的焦点在x轴上,过点M作两条直线 分别交抛物线于A,B两点(纵坐标均为非负数),若直线
分别交抛物线于A,B两点(纵坐标均为非负数),若直线 与
与 的倾斜角互补,求
的倾斜角互补,求 面积的最大值.
面积的最大值.
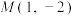 是抛物线上一点.
是抛物线上一点.(1)求抛物线方程;
(2)若抛物线的焦点在x轴上,过点M作两条直线
 分别交抛物线于A,B两点(纵坐标均为非负数),若直线
分别交抛物线于A,B两点(纵坐标均为非负数),若直线 与
与 的倾斜角互补,求
的倾斜角互补,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
名校
9 . 已知函数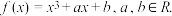
(1)若关于x的方程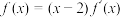 有3个不等实根,求
有3个不等实根,求 的取值范围;
的取值范围;
(2)若关于x的不等式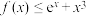 对一切实数x恒成立,求ab的最大值.
对一切实数x恒成立,求ab的最大值.
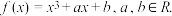
(1)若关于x的方程
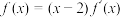 有3个不等实根,求
有3个不等实根,求 的取值范围;
的取值范围;(2)若关于x的不等式
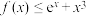 对一切实数x恒成立,求ab的最大值.
对一切实数x恒成立,求ab的最大值.
您最近一年使用:0次
2022-07-20更新
|
287次组卷
|
3卷引用:贵州省黔东南州2021-2022学年度高二下学期期末联考数学(理)试题
名校
10 . 已知 ,
,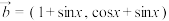 ,函数
,函数
(1)求 的周期和单调递减区间;
的周期和单调递减区间;
(2)设 为常数,若
为常数,若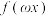 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(3)设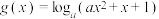 定义域为
定义域为 ,若对任意
,若对任意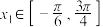 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值.
的取值.
 ,
,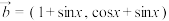 ,函数
,函数
(1)求
 的周期和单调递减区间;
的周期和单调递减区间;(2)设
 为常数,若
为常数,若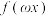 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;(3)设
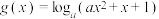 定义域为
定义域为 ,若对任意
,若对任意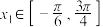 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值.
的取值.
您最近一年使用:0次
2022-07-15更新
|
1689次组卷
|
7卷引用:贵州省遵义市2021-2022学年高一下学期期末质量监测数学试题
贵州省遵义市2021-2022学年高一下学期期末质量监测数学试题贵州省遵义市2021-2022学年高一下学期期末质量监测数学试题江西省赣州市赣县第三中学2022-2023学年高一上学期10月月考数学(理)试题(已下线)高一下学期期末真题精选(压轴60题20个考点专练)(已下线)上海市高一下学期期末真题必刷04-期末考点大串讲(沪教版2020必修二)四川省仁寿第一中学校南校区2022-2023学年高一下学期期中考试数学试题 甘肃省白银市靖远县第四中学2022-2023学年高一下学期6月月考数学试题



