名校
1 . 已知函数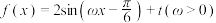 ,且
,且 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为 ,图象过点
,图象过点 .
.
(1)求 的表达式和
的表达式和 的单调增区间;
的单调增区间;
(2)若函数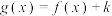 在区间
在区间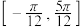 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围.
的取值范围.
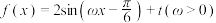 ,且
,且 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为 ,图象过点
,图象过点 .
.(1)求
 的表达式和
的表达式和 的单调增区间;
的单调增区间;(2)若函数
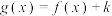 在区间
在区间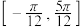 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-02-13更新
|
1388次组卷
|
5卷引用:湖北省襄阳市第一中学2022-2023学年高一下学期4月月考数学试题
名校
解题方法
2 . 设定义在实数集 上的函数
上的函数 ,
, 恒不为0,若存在不等于1的正常数
恒不为0,若存在不等于1的正常数 ,对于任意实数
,对于任意实数 ,等式
,等式 恒成立,则称函数
恒成立,则称函数 为
为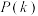 函数.
函数.
(1)若函数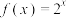 为
为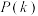 函数,求出
函数,求出 的值;
的值;
(2)设 ,其中
,其中 为自然对数的底数,函数
为自然对数的底数,函数 .
.
①比较 与
与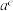 的大小;
的大小;
②判断函数 是否为
是否为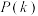 函数,若是,请证明;若不是,试说明理由.
函数,若是,请证明;若不是,试说明理由.
 上的函数
上的函数 ,
, 恒不为0,若存在不等于1的正常数
恒不为0,若存在不等于1的正常数 ,对于任意实数
,对于任意实数 ,等式
,等式 恒成立,则称函数
恒成立,则称函数 为
为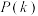 函数.
函数.(1)若函数
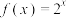 为
为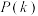 函数,求出
函数,求出 的值;
的值;(2)设
 ,其中
,其中 为自然对数的底数,函数
为自然对数的底数,函数 .
.①比较
 与
与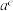 的大小;
的大小;②判断函数
 是否为
是否为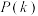 函数,若是,请证明;若不是,试说明理由.
函数,若是,请证明;若不是,试说明理由.
您最近一年使用:0次
2020-02-13更新
|
1245次组卷
|
7卷引用:河南省信阳高级中学2022-2023学年高一上学期1月测试(一)数学试题
3 . 已知 的面积等于1,若
的面积等于1,若 ,则当这个三角形的三条高的乘积取最大值时,
,则当这个三角形的三条高的乘积取最大值时,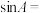
______
 的面积等于1,若
的面积等于1,若 ,则当这个三角形的三条高的乘积取最大值时,
,则当这个三角形的三条高的乘积取最大值时,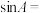
您最近一年使用:0次
2019-09-18更新
|
4641次组卷
|
12卷引用:黑龙江省鹤岗市第一中学2022-2023学年高一下学期期中数学试题
黑龙江省鹤岗市第一中学2022-2023学年高一下学期期中数学试题苏教版(2019) 必修第二册 必杀技 第11章 解三角形 11.2 正弦定理 第11.2 节综合训练【课后练】 第1.6节综合训练 课后作业-湘教版(2019)必修(第二册)第1章 平面向量及其应用2020年1月中学生标准学术能力诊断性测试诊断性测试理科数学试卷中学生标准学术能力诊断性测试2019-2020学年高三1月(一卷)数学(理)试题(已下线)专题01 少丢分题目强化卷(第二篇)-备战2021年新高考数学分层强化训练(北京专版)重庆市2021届高三上学期第二次预测性考试数学试题(已下线)专题4-2 正余弦定理与解三角形小题归类1-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)四川省泸州市泸县第四中学2022届高三三诊模拟考试理科数学试题(已下线)必刷卷01 (理)-2022年高考数学考前信息必刷卷(全国乙卷)浙江省名校协作体2019-2020学年高三第一学期第一次联考数学试题(已下线)专题19 解三角形中的面积问题
名校
解题方法
4 . 已知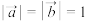 ,
,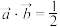 ,
,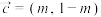 ,
,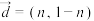 (m,
(m,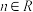 ).存在
).存在 ,
, ,对于任意实数m,n,不等式
,对于任意实数m,n,不等式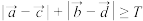 恒成立,则实数T的取值范围为
恒成立,则实数T的取值范围为
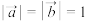 ,
,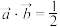 ,
,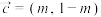 ,
,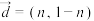 (m,
(m,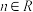 ).存在
).存在 ,
, ,对于任意实数m,n,不等式
,对于任意实数m,n,不等式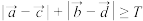 恒成立,则实数T的取值范围为
恒成立,则实数T的取值范围为A. | B.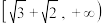 | C.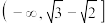 | D. |
您最近一年使用:0次
2020-04-18更新
|
2533次组卷
|
3卷引用:高一下期中真题精选(压轴60题专练)
5 . (1)在 中,内角A,B,C的对边分别为a,b,c,R表示
中,内角A,B,C的对边分别为a,b,c,R表示 的外接圆半径.
的外接圆半径.
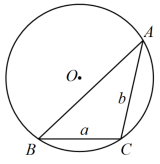
①如图,在以O圆心、半径为2的圆O中, 和
和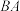 是圆O的弦,其中
是圆O的弦,其中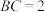 ,
, ,求弦
,求弦 的长;
的长;
②在 中,若
中,若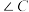 是钝角,求证:
是钝角,求证: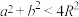 ;
;
(2)给定三个正实数a、b、R,其中 ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.
 中,内角A,B,C的对边分别为a,b,c,R表示
中,内角A,B,C的对边分别为a,b,c,R表示 的外接圆半径.
的外接圆半径.①如图,在以O圆心、半径为2的圆O中,
 和
和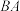 是圆O的弦,其中
是圆O的弦,其中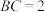 ,
, ,求弦
,求弦 的长;
的长;②在
 中,若
中,若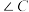 是钝角,求证:
是钝角,求证: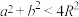 ;
;
(2)给定三个正实数a、b、R,其中
 ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.
您最近一年使用:0次
2020-04-17更新
|
1701次组卷
|
15卷引用:第六章 平面向量及其应用(基础、典型、易错、压轴)分类专项训练(3)
(已下线)第六章 平面向量及其应用(基础、典型、易错、压轴)分类专项训练(3)【全国百强校】福建省福州第三中学2017-2018学年高一下学期(实验班)期末考试数学试题上海市曹杨二中2018-2019学年高一下期末数学试题(已下线)上海市华师大二附中2015-2016学年高一下学期期中数学试题江苏省南通中学2018-2019学年高一下学期期中数学试题江苏省扬州中学2019-2020学年高一下学期6月月考数学试题(已下线)第6章三角(能力提升)-2020-2021学年高一数学下册单元测试定心卷(沪教版2020必修第二册)(已下线)第19讲压轴综合题(讲义)-【教育机构专用】2021年春季高一数学辅导讲义(沪教版2020必修第二册)湖南省怀化市第三中学2020-2021学年高一下学期期中数学试题(已下线)上海期末真题精选50题(大题压轴版)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)(已下线)大题好拿分期中考前必做30题(压轴版)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)(已下线)第20讲 期末复习(练习)提升卷-【教育机构专用】2021年春季高一数学辅导讲义(沪教版2020必修第二册)(已下线)6.4平面向量的应用C卷湖南省长沙市明德中学2021-2022学年高一下学期期中数学试题上海市复旦大学附属中学2022-2023学年高二上学期开学考试数学试题
名校
6 . 奔驰定理:已知 是
是 内的一点,
内的一点,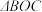 ,
,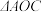 ,
,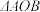 的面积分别为
的面积分别为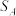 ,
,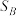 ,
,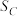 ,则
,则 .“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedes benz)的logo很相似,故形象地称其为“奔驰定理”若
.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedes benz)的logo很相似,故形象地称其为“奔驰定理”若 是锐角
是锐角 内的一点,
内的一点, ,
, ,
, 是
是 的三个内角,且点
的三个内角,且点 满足
满足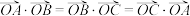 ,则必有( )
,则必有( )
 是
是 内的一点,
内的一点,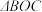 ,
,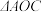 ,
,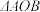 的面积分别为
的面积分别为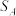 ,
,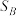 ,
,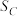 ,则
,则 .“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedes benz)的logo很相似,故形象地称其为“奔驰定理”若
.“奔驰定理”是平面向量中一个非常优美的结论,因为这个定理对应的图形与“奔驰”轿车(Mercedes benz)的logo很相似,故形象地称其为“奔驰定理”若 是锐角
是锐角 内的一点,
内的一点, ,
, ,
, 是
是 的三个内角,且点
的三个内角,且点 满足
满足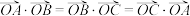 ,则必有( )
,则必有( )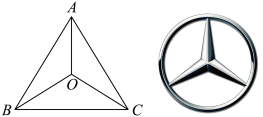
A.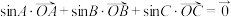 |
B. |
C.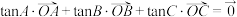 |
D. |
您最近一年使用:0次
2019-12-04更新
|
3111次组卷
|
6卷引用:平面向量专题:奔驰定理解三角形面积比值问题-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)
(已下线)平面向量专题:奔驰定理解三角形面积比值问题-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)湖南省邵阳市武冈市2021-2022学年高一下学期期中数学试题(已下线)第五篇 向量与几何 专题13 奔驰定理 微点2 奔驰定理(二)河北省保定市第一中学2024-2025学年高一(第八届贯通班)上学期开学考试数学试题河南省南阳市2019-2020学年高三上学期期中数学(理)试题(已下线)专题突破卷15 三角形的“四心”及奔驰定理
7 . 已知 的外接圆圆心为O,
的外接圆圆心为O,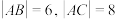 ,
,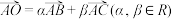 ,若
,若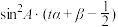 (
( 为实数)有最小值,则参数
为实数)有最小值,则参数 的取值范围是
的取值范围是______ .
 的外接圆圆心为O,
的外接圆圆心为O,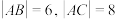 ,
,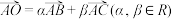 ,若
,若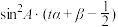 (
( 为实数)有最小值,则参数
为实数)有最小值,则参数 的取值范围是
的取值范围是
您最近一年使用:0次
2019-11-19更新
|
3188次组卷
|
12卷引用:上海市上海中学2022-2023学年高一下学期期末数学试题
上海市上海中学2022-2023学年高一下学期期末数学试题山西省长治市第二中学校2019-2020学年高一下学期摸底数学(理)试题湖北省温德克英联盟2023-2024学年高二8月开学综合性难度选拔考试数学试题(已下线)上海市高一下学期期末真题必刷03-期末考点大串讲(沪教版2020必修二)湖北省武汉市东西湖区华中师范大学第一附属中学2019-2020学年高三上学期期中数学(理)试题(已下线)3.1平面向量的概念及其性质[文] -《备战2020年高考精选考点专项突破题集》(已下线)3.1平面向量的概念及其性质[理]-《备战2020年高考精选考点专项突破题集》2020届安徽省淮北市濉溪县高三上学期第二次教学质量检测数学(理)试题2020届湖南省长沙市长郡中学高三月考(六)数学(理)试题河北省衡水市枣强中学2020届高三下学期2月调研数学(理)试题(已下线)上海市浦东新区华东师范大学第二附属中学2021届高三4月高考数学模拟试题(已下线)上海市华东师范大学第二附属中学2021届高三下学期4月月考数学试题
名校
8 . 已知函数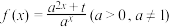 是奇函数.
是奇函数.
(1)求实数 的值;
的值;
(2)若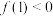 ,对任意
,对任意 有
有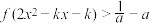 恒成立,求实数
恒成立,求实数 取值范围;
取值范围;
(3)设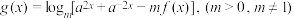 ,若
,若 ,问是否存在实数
,问是否存在实数 使函数
使函数 在
在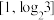 上的最大值为
上的最大值为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
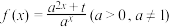 是奇函数.
是奇函数.(1)求实数
 的值;
的值;(2)若
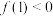 ,对任意
,对任意 有
有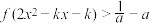 恒成立,求实数
恒成立,求实数 取值范围;
取值范围;(3)设
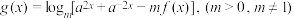 ,若
,若 ,问是否存在实数
,问是否存在实数 使函数
使函数 在
在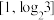 上的最大值为
上的最大值为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
2019-11-08更新
|
2582次组卷
|
5卷引用:江西省宜春市宜春中学2023-2024学年高一上学期期末数学试题
名校
9 . 已知 为锐角三角形,满足
为锐角三角形,满足 ,
, 外接圆的圆心为
外接圆的圆心为 ,半径为1,则
,半径为1,则 的取值范围是
的取值范围是______ .
 为锐角三角形,满足
为锐角三角形,满足 ,
, 外接圆的圆心为
外接圆的圆心为 ,半径为1,则
,半径为1,则 的取值范围是
的取值范围是
您最近一年使用:0次
2019-10-31更新
|
7179次组卷
|
9卷引用:广东省肇庆市第一中学2022-2023学年高一下学期期中数学试题
广东省肇庆市第一中学2022-2023学年高一下学期期中数学试题黑龙江省哈尔滨市实验中学2022-2023学年高一下学期第一次月考数学试卷湖北省随州市第一中学2020-2021学年高一下学期期中数学试题湖北省武汉市钢城第四中学2021-2022学年高一下学期期中数学试题辽宁省沈阳市东北育才学校科学高中部2021-2022学年高一下学期阶段测试数学试题湖北省温德克英联盟2023-2024学年高二8月开学综合性难度选拔考试数学试题辽宁省沈阳市沈河区第二中学2019年高三上学期10月月考数学(理)试题江西省宜春市上高二中2019-2020学年高三上学期第四次月考数学(理)试题(已下线)专题05 三角形中最值问题的两条捷径-备战2020年高考数学二轮痛点突破专项归纳与提高
名校
10 . 对于函数 ,若
,若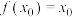 ,则称
,则称 为
为 的“不动点”,若
的“不动点”,若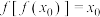 ,则称
,则称 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即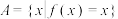 ,
,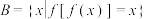 ,那么,
,那么,
(1)求函数 的“稳定点”;
的“稳定点”;
(2)求证: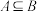 ;
;
(3)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 ,若
,若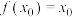 ,则称
,则称 为
为 的“不动点”,若
的“不动点”,若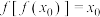 ,则称
,则称 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即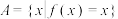 ,
,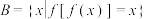 ,那么,
,那么,(1)求函数
 的“稳定点”;
的“稳定点”;(2)求证:
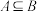 ;
;(3)若
 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2019-10-25更新
|
1045次组卷
|
6卷引用:四川省成都市嘉祥教育集团2023-2024学年高一上学期期中考试数学试题



