2011·广东广州·高考模拟
名校
1 . 将正整数12分解成两个正整数的乘积有 ,
, ,
, 三种,其中
三种,其中 是这三种分解中,两数差的绝对值最小的,我们称
是这三种分解中,两数差的绝对值最小的,我们称 为12的最佳分解.当
为12的最佳分解.当 是正整数
是正整数 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数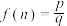 ,例如
,例如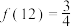 .关于函数
.关于函数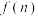 有下列叙述:①
有下列叙述:①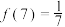 ,②
,②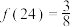 ,③
,③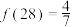 ,④
,④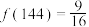 .其中正确的序号为
.其中正确的序号为_____ (填入所有正确的序号).
 ,
, ,
, 三种,其中
三种,其中 是这三种分解中,两数差的绝对值最小的,我们称
是这三种分解中,两数差的绝对值最小的,我们称 为12的最佳分解.当
为12的最佳分解.当 是正整数
是正整数 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数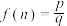 ,例如
,例如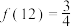 .关于函数
.关于函数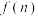 有下列叙述:①
有下列叙述:①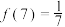 ,②
,②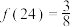 ,③
,③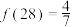 ,④
,④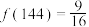 .其中正确的序号为
.其中正确的序号为
您最近一年使用:0次
名校
解题方法
2 . 若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足
都满足 和
和 恒成立,则称直线
恒成立,则称直线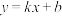 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数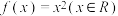 ,
,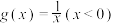 ,
, ,则有下列命题:
,则有下列命题:
①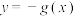 与
与 有“隔离直线”;
有“隔离直线”;
② 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为 ;
;
③ 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是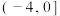 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”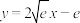 .
.
其中真命题的序号为_______________________ .(请填上所有正确命题的序号)
 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足
都满足 和
和 恒成立,则称直线
恒成立,则称直线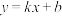 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数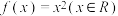 ,
,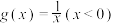 ,
, ,则有下列命题:
,则有下列命题:①
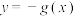 与
与 有“隔离直线”;
有“隔离直线”;②
 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为 ;
;③
 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是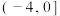 ;
;④
 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”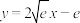 .
.其中真命题的序号为
您最近一年使用:0次
2021-01-16更新
|
852次组卷
|
5卷引用:上海市浦东新区上海海事大学附属北蔡高级中学2024届高三上学期期中数学试题
名校
3 . 对函数 (其中
(其中 为实数,
为实数,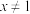 ),给出下列命题;
),给出下列命题;
①当 时,
时, 在定义域上为单调递减函数;②对任意
在定义域上为单调递减函数;②对任意 ,
, 都不是奇函数;③当
都不是奇函数;③当 时,
时, 为偶函数;④关于
为偶函数;④关于 的方程
的方程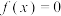 最多有一个实数根,其中正确命题的序号为
最多有一个实数根,其中正确命题的序号为________ ,(把所有正确的命题序号写入横线)
 (其中
(其中 为实数,
为实数,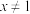 ),给出下列命题;
),给出下列命题;①当
 时,
时, 在定义域上为单调递减函数;②对任意
在定义域上为单调递减函数;②对任意 ,
, 都不是奇函数;③当
都不是奇函数;③当 时,
时, 为偶函数;④关于
为偶函数;④关于 的方程
的方程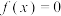 最多有一个实数根,其中正确命题的序号为
最多有一个实数根,其中正确命题的序号为
您最近一年使用:0次
2011·广西桂林·一模
名校
4 . 给出下列四个命题:
①过平面外一点,作与该平面成 角的直线一定有无穷多条;
角的直线一定有无穷多条;
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面分别与这两条直线所成的角相等;
其中正确的命题序号为______ (请把所有正确命题的序号都填上).
①过平面外一点,作与该平面成
 角的直线一定有无穷多条;
角的直线一定有无穷多条;②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面分别与这两条直线所成的角相等;
其中正确的命题序号为
您最近一年使用:0次
名校
5 . 设直线系 :
: ,对于下列三个命题:
,对于下列三个命题:
① 中所有直线均与一个定圆相切;
中所有直线均与一个定圆相切;
② 中所有直线均经过一个定点;
中所有直线均经过一个定点;
③存在点 不在
不在 中的任一条直线上.
中的任一条直线上.
其中真命题的序号为____________ (写出所有真命题的序号)
 :
: ,对于下列三个命题:
,对于下列三个命题:①
 中所有直线均与一个定圆相切;
中所有直线均与一个定圆相切;②
 中所有直线均经过一个定点;
中所有直线均经过一个定点;③存在点
 不在
不在 中的任一条直线上.
中的任一条直线上.其中真命题的序号为
您最近一年使用:0次
名校
6 . 已知正方体 的边长为2,点E,F分别是线段
的边长为2,点E,F分别是线段 ,
, 的中点,平面
的中点,平面 过点
过点 ,E,F,且与正方体
,E,F,且与正方体 形成一个截面,现有如下说法:
形成一个截面,现有如下说法:
①截面图形是一个六边形;
②棱 与平面
与平面 的交点是
的交点是 的中点;
的中点;
③若点I在正方形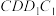 内(含边界位置),且
内(含边界位置),且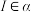 ,则点
,则点 的轨迹长度为
的轨迹长度为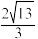 ;
;
④截面图形的周长为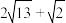 ;
;
则上述说法正确的命题序号为___________ .
 的边长为2,点E,F分别是线段
的边长为2,点E,F分别是线段 ,
, 的中点,平面
的中点,平面 过点
过点 ,E,F,且与正方体
,E,F,且与正方体 形成一个截面,现有如下说法:
形成一个截面,现有如下说法:①截面图形是一个六边形;
②棱
 与平面
与平面 的交点是
的交点是 的中点;
的中点;③若点I在正方形
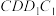 内(含边界位置),且
内(含边界位置),且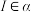 ,则点
,则点 的轨迹长度为
的轨迹长度为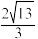 ;
;④截面图形的周长为
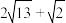 ;
;则上述说法正确的命题序号为
您最近一年使用:0次
2021-11-06更新
|
504次组卷
|
6卷引用:上海市进才中学2021-2022学年高二上学期期中数学试题
名校
7 . 某公园草坪上有一扇形小径(如图),扇形半径为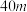 ,中心角为
,中心角为 ,甲由扇形中心
,甲由扇形中心 出发沿
出发沿 以每秒2米的速度向
以每秒2米的速度向 快走,同时乙从
快走,同时乙从 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒 米的速度向
米的速度向 慢跑,记
慢跑,记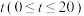 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为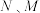 ,
, ,通过计算
,通过计算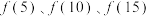 ,判断下列说法是否正确:
,判断下列说法是否正确:

(1)当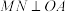 时,函数
时,函数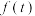 取最小值;
取最小值;
(2)函数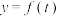 在区间
在区间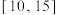 上是增函数;
上是增函数;
(3)若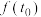 最小,则
最小,则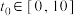 ;
;
(4)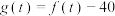 在
在 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______ (把你认为正确的判断序号都填上)
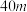 ,中心角为
,中心角为 ,甲由扇形中心
,甲由扇形中心 出发沿
出发沿 以每秒2米的速度向
以每秒2米的速度向 快走,同时乙从
快走,同时乙从 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒 米的速度向
米的速度向 慢跑,记
慢跑,记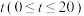 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为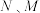 ,
, ,通过计算
,通过计算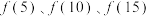 ,判断下列说法是否正确:
,判断下列说法是否正确:
(1)当
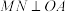 时,函数
时,函数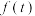 取最小值;
取最小值;(2)函数
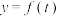 在区间
在区间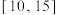 上是增函数;
上是增函数;(3)若
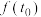 最小,则
最小,则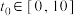 ;
;(4)
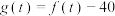 在
在 上至少有两个零点;
上至少有两个零点;其中正确的判断序号是
您最近一年使用:0次
2019-11-14更新
|
260次组卷
|
3卷引用:上海市上海师范大学附属中学2018-2019学年高三上学期10月月考数学试题
名校
8 . 下列说法中:
①“若 ,则
,则 ”的否命题是“若
”的否命题是“若 ,则
,则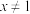 ”;
”;
②“ ”是“
”是“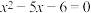 ”的必要非充分条件;
”的必要非充分条件;
③“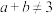 ”是“
”是“ 或
或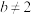 ”的充分非必要条件;
”的充分非必要条件;
④“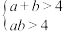 ”是“
”是“ 且
且 ”的充要条件.
”的充要条件.
其中正确的序号为__________ .
①“若
 ,则
,则 ”的否命题是“若
”的否命题是“若 ,则
,则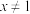 ”;
”;②“
 ”是“
”是“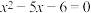 ”的必要非充分条件;
”的必要非充分条件;③“
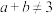 ”是“
”是“ 或
或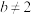 ”的充分非必要条件;
”的充分非必要条件;④“
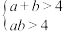 ”是“
”是“ 且
且 ”的充要条件.
”的充要条件.其中正确的序号为
您最近一年使用:0次
9 . 如图,在棱长为1的正方体 中,
中, 、
、 、
、 分别为线段
分别为线段 、
、 、
、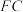 的中点,下述四个结论:
的中点,下述四个结论: 、
、 、
、 共点;
共点;
②直线 、
、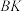 为异面直线;
为异面直线;
③四面体 的体积为
的体积为 ;
;
④线段 上存在一点
上存在一点 使得直线
使得直线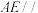 平面
平面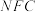 .
.
其中所有正确结论的序号为___________ .
 中,
中, 、
、 、
、 分别为线段
分别为线段 、
、 、
、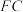 的中点,下述四个结论:
的中点,下述四个结论: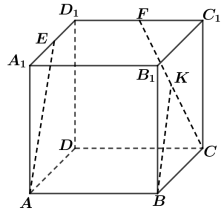
 、
、 、
、 共点;
共点;②直线
 、
、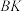 为异面直线;
为异面直线;③四面体
 的体积为
的体积为 ;
;④线段
 上存在一点
上存在一点 使得直线
使得直线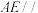 平面
平面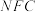 .
.其中所有正确结论的序号为
您最近一年使用:0次
2021-06-05更新
|
1632次组卷
|
4卷引用:上海市浦东新区南汇中学2021-2022学年高二上学期10月月考数学试题
上海市浦东新区南汇中学2021-2022学年高二上学期10月月考数学试题四川省成都市第七中学2021届高三5月高考热身考试理科数学试题(已下线)第23节 空间几何体的表面积与体积(已下线)第04讲线线、线面、面面平行的判定与性质(核心考点讲与练)(3)
名校
10 . 给出下列命题:
①若两条不同的直线垂直于第三条直线,则这两条直线互相平行;
②若两个不同的平面垂直于一条直线,则这两个平面互相平行;
③若一条直线平行于一个平面,另一条直线与这个平面垂直,则这两条直线互相垂直.
其中所有正确命题的序号为___________ .
①若两条不同的直线垂直于第三条直线,则这两条直线互相平行;
②若两个不同的平面垂直于一条直线,则这两个平面互相平行;
③若一条直线平行于一个平面,另一条直线与这个平面垂直,则这两条直线互相垂直.
其中所有正确命题的序号为
您最近一年使用:0次
2021-05-10更新
|
739次组卷
|
7卷引用:上海市实验学校2023届高三下学期开学考试数学试题
上海市实验学校2023届高三下学期开学考试数学试题上海市虹口区2021届高三二模数学试题上海市嘉定区第一中学、金山中学2021-2022学年高二上学期9月月考数学试题(已下线)考向23 点、直线、平面之间的位置关系-备战2022年高考数学一轮复习考点微专题(上海专用)上海市文来中学2021-2022学年高二上学期期中数学试题(已下线)第19讲 立体几何初步-3上海外国语大学附属外国语学校2021-2022学年高二上学期期中数学试题



