名校
解题方法
1 . 如图,在正四棱柱 中,
中, ,
,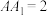 ,
, 是
是 的中点.
的中点.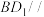 平面
平面 ;
;
(2)证明: ;
;
(3)求点 到平面
到平面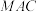 的距离.
的距离.
 中,
中, ,
,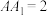 ,
, 是
是 的中点.
的中点.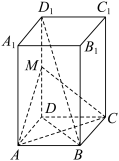
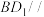 平面
平面 ;
;(2)证明:
 ;
;(3)求点
 到平面
到平面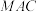 的距离.
的距离.
您最近一年使用:0次
2024-08-30更新
|
983次组卷
|
2卷引用:北京东直门中学2023-2024学年高一下学期6月月考数学试题
2 . 我们知道,在平面内取定单位正交基底建立坐标系后,任意一个平面向量,都可以用二元有序实数对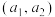 表示.平面向量又称为二维向量,一般地,n元有序实数组
表示.平面向量又称为二维向量,一般地,n元有序实数组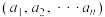 称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,可定义两个向量的数量积,向量的长度(模)等:设
称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,可定义两个向量的数量积,向量的长度(模)等:设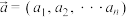 ,
,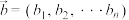 ,则
,则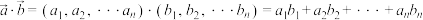 ;
;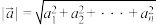 .已知向量
.已知向量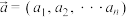 满足
满足 ,向量
,向量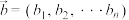 满足
满足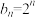
(1)求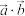 的值;
的值;
(2)若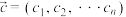 ,其中
,其中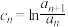 .
.
(i)求证: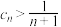 ;
;
(ii)当 且
且 时,证明:
时,证明: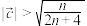 .
.
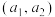 表示.平面向量又称为二维向量,一般地,n元有序实数组
表示.平面向量又称为二维向量,一般地,n元有序实数组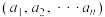 称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,可定义两个向量的数量积,向量的长度(模)等:设
称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,可定义两个向量的数量积,向量的长度(模)等:设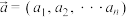 ,
,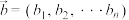 ,则
,则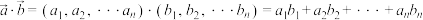 ;
;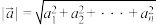 .已知向量
.已知向量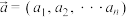 满足
满足 ,向量
,向量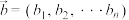 满足
满足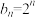
(1)求
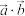 的值;
的值;(2)若
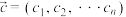 ,其中
,其中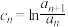 .
.(i)求证:
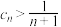 ;
;(ii)当
 且
且 时,证明:
时,证明: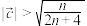 .
.
您最近一年使用:0次
2024-09-27更新
|
799次组卷
|
6卷引用:滚动月考卷2 周测1---周测13 (一轮好卷北京专版 )
(已下线)滚动月考卷2 周测1---周测13 (一轮好卷北京专版 )吉林省长春市第八中学2025届高三上学期一模数学试卷(已下线)考点26 导数的应用--不等式问题 --高考数学100个黄金考点(2025届)【讲】(已下线)滚动月考卷2 (高三大一轮好卷基础卷)(已下线)第四节 数列的求和【同步课时】(高三一轮北京专版)宁夏回族自治区石嘴山市2024-2025学年高三上学期10月期中教学质量检测数学试题
3 . 集合论在离散数学中有着非常重要的地位.对于非空集合 和
和 ,定义和集
,定义和集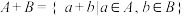 ,用符号
,用符号 表示和集
表示和集 内的元素个数.
内的元素个数.
(1)已知集合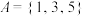 ,
,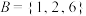 ,
,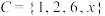 ,若
,若 ,求
,求 的值;
的值;
(2)记集合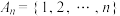 ,
,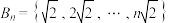 ,
,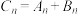 ,
, 为
为 中所有元素之和,
中所有元素之和, ,求证:
,求证: ;
;
(3)若 与
与 都是由
都是由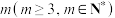 个整数构成的集合,且
个整数构成的集合,且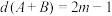 ,证明:若按一定顺序排列,集合
,证明:若按一定顺序排列,集合 与
与 中的元素是两个公差相等的等差数列.
中的元素是两个公差相等的等差数列.
 和
和 ,定义和集
,定义和集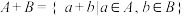 ,用符号
,用符号 表示和集
表示和集 内的元素个数.
内的元素个数.(1)已知集合
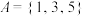 ,
,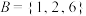 ,
,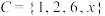 ,若
,若 ,求
,求 的值;
的值;(2)记集合
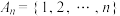 ,
,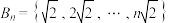 ,
,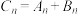 ,
, 为
为 中所有元素之和,
中所有元素之和, ,求证:
,求证: ;
;(3)若
 与
与 都是由
都是由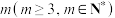 个整数构成的集合,且
个整数构成的集合,且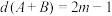 ,证明:若按一定顺序排列,集合
,证明:若按一定顺序排列,集合 与
与 中的元素是两个公差相等的等差数列.
中的元素是两个公差相等的等差数列.
您最近一年使用:0次
2024-06-07更新
|
782次组卷
|
3卷引用:北京市第八中学2024-2025学年高三上学期暑假第一阶段(开学)练习数学试题
4 . 已知函数 ,曲线
,曲线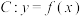 在点
在点 处的切线为
处的切线为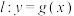 ,记
,记 .
.
(1)当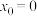 时,求切线
时,求切线 的方程;
的方程;
(2)在(1)的条件下,求函数 的零点并证明
的零点并证明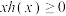 ;
;
(3)当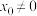 时,直接写出函数
时,直接写出函数 的零点个数.(结论不要求证明)
的零点个数.(结论不要求证明)
 ,曲线
,曲线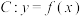 在点
在点 处的切线为
处的切线为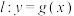 ,记
,记 .
.(1)当
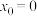 时,求切线
时,求切线 的方程;
的方程;(2)在(1)的条件下,求函数
 的零点并证明
的零点并证明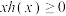 ;
;(3)当
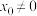 时,直接写出函数
时,直接写出函数 的零点个数.(结论不要求证明)
的零点个数.(结论不要求证明)
您最近一年使用:0次
5 . 已知函数 ,
,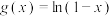 .
.
(1)求证: 为偶函数;
为偶函数;
(2)设 ,判断
,判断 的单调性,并用单调性定义加以证明.
的单调性,并用单调性定义加以证明.
 ,
,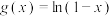 .
.(1)求证:
 为偶函数;
为偶函数;(2)设
 ,判断
,判断 的单调性,并用单调性定义加以证明.
的单调性,并用单调性定义加以证明.
您最近一年使用:0次
6 . 已知函数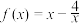 .
.
(1)求证函数 为奇函数;
为奇函数;
(2)判断 在区间
在区间 上的单调性,并用定义进行证明;
上的单调性,并用定义进行证明;
(3)求 在区间[2,6]上的最大值与最小值.
在区间[2,6]上的最大值与最小值.
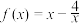 .
.(1)求证函数
 为奇函数;
为奇函数;(2)判断
 在区间
在区间 上的单调性,并用定义进行证明;
上的单调性,并用定义进行证明;(3)求
 在区间[2,6]上的最大值与最小值.
在区间[2,6]上的最大值与最小值.
您最近一年使用:0次
7 . 已知函数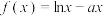 (a为常数).
(a为常数).
(1)求函数 的单调区间;
的单调区间;
(2)若存在两个不相等的正数 ,
, 满足
满足 ,求证:
,求证: .
.
(3)若 有两个零点
有两个零点 ,
, ,证明:
,证明: .
.
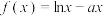 (a为常数).
(a为常数).(1)求函数
 的单调区间;
的单调区间;(2)若存在两个不相等的正数
 ,
, 满足
满足 ,求证:
,求证: .
.(3)若
 有两个零点
有两个零点 ,
, ,证明:
,证明: .
.
您最近一年使用:0次
2023-12-30更新
|
1989次组卷
|
11卷引用:北京市丰台区怡海中学2024-2025学年高三上学期11月期中考试数学试题
北京市丰台区怡海中学2024-2025学年高三上学期11月期中考试数学试题黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期期中数学试题(已下线)5.3 导数在研究函数中的应用(练习)-高二数学同步精品课堂(苏教版2019选择性必修第一册)福建省宁德市福安市福安一中2023-2024学年高三上学期10月月考数学试题(已下线)模块三 大招24 对数平均不等式(已下线)模块三 大招10 对数平均不等式重庆缙云教育联盟2024届高三高考第一次诊断性检测数学试卷(已下线)模块五 专题6 全真拔高模拟6(已下线)模块2专题7 对数均值不等式 巧妙解决双变量练(已下线)专题6 导数与零点偏移【练】(已下线)专题16 对数平均不等式及其应用【讲】
名校
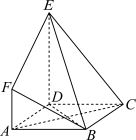
8 . 如图,在多面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,平面
的正方形,平面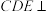 平面
平面 ,
, ,
, ,
, .
. 平面
平面 ;
;
(2)求平面 与平面
与平面 夹角的余弦值;
夹角的余弦值;
(3)线段 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
 中,四边形
中,四边形 是边长为
是边长为 的正方形,平面
的正方形,平面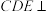 平面
平面 ,
, ,
, ,
, .
.
 平面
平面 ;
;(2)求平面
 与平面
与平面 夹角的余弦值;
夹角的余弦值;(3)线段
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
您最近一年使用:0次
2023-11-03更新
|
606次组卷
|
3卷引用:北京市丰台区2023-2024学年高二上学期期中练习数学试题(A)
名校
9 .  个有次序的实数
个有次序的实数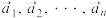 所组成的有序数组
所组成的有序数组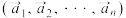 称为一个
称为一个 维向量,其中
维向量,其中 称为该向量的第
称为该向量的第 个分量.特别地,对一个
个分量.特别地,对一个 维向量
维向量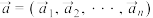 ,若
,若 ,称
,称 为
为 维信号向量.设
维信号向量.设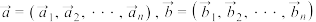 ,则
,则 和
和 的内积定义为
的内积定义为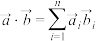 ,且
,且 .
.
(1)直接写出4个两两垂直的4维信号向量.
(2)证明:不存在14个两两垂直的14维信号向量.
(3)已知 个两两垂直的2024维信号向量
个两两垂直的2024维信号向量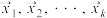 满足它们的前
满足它们的前 个分量都是相同的,求证:
个分量都是相同的,求证: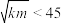 .
.
 个有次序的实数
个有次序的实数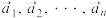 所组成的有序数组
所组成的有序数组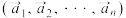 称为一个
称为一个 维向量,其中
维向量,其中 称为该向量的第
称为该向量的第 个分量.特别地,对一个
个分量.特别地,对一个 维向量
维向量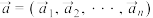 ,若
,若 ,称
,称 为
为 维信号向量.设
维信号向量.设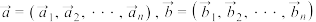 ,则
,则 和
和 的内积定义为
的内积定义为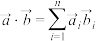 ,且
,且 .
.(1)直接写出4个两两垂直的4维信号向量.
(2)证明:不存在14个两两垂直的14维信号向量.
(3)已知
 个两两垂直的2024维信号向量
个两两垂直的2024维信号向量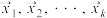 满足它们的前
满足它们的前 个分量都是相同的,求证:
个分量都是相同的,求证: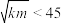 .
.
您最近一年使用:0次
2023-11-15更新
|
425次组卷
|
7卷引用:北京市西城区北京师范大学附属实验中学2023-2024学年高二上学期期中考试数学试题
北京市西城区北京师范大学附属实验中学2023-2024学年高二上学期期中考试数学试题北京市北京师范大学附属中学2023-2024学年高二上学期数学期中考试数学试题北京市第十一中学2023-2024学年高一下学期期中练习数学试卷(已下线)第3章 空间向量及其应用(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)(已下线)模块三 专题2 专题1 平面向量运算(已下线)模块三 专题2 解答题分类练 专题3 平面向量各类运算(解答题)安徽省合肥市普通高中六校联盟2023-2024学年高一下学期期末联考数学试卷
名校
解题方法
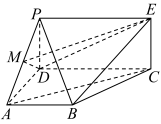
10 . 如图,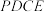 为矩形,
为矩形, 为梯形,平面
为梯形,平面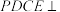 平面
平面 ,
,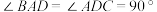 ,
,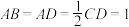 ,
,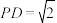 .
. 中点,求证:
中点,求证: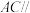 平面
平面 ;
;
(2)求直线 与直线
与直线 所成角的大小;
所成角的大小;
(3)设平面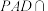 平面
平面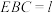 ,试判断l与平面
,试判断l与平面 能否垂直?并证明你的结论.
能否垂直?并证明你的结论.
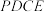 为矩形,
为矩形, 为梯形,平面
为梯形,平面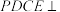 平面
平面 ,
,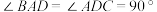 ,
,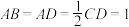 ,
, .
.
 中点,求证:
中点,求证: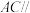 平面
平面 ;
;(2)求直线
 与直线
与直线 所成角的大小;
所成角的大小;(3)设平面
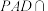 平面
平面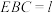 ,试判断l与平面
,试判断l与平面 能否垂直?并证明你的结论.
能否垂直?并证明你的结论.
您最近一年使用:0次
2023-10-17更新
|
465次组卷
|
2卷引用:北京市八一学校2023-2024学年高二上学期10月月考数学试题



