解题方法
1 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极值;
的极值;
(3)若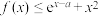 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)当
 时,求
时,求 的极值;
的极值;(3)若
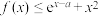 恒成立,求
恒成立,求 的取值范围.
的取值范围.
您最近一年使用:0次
2 . 已知函数 有两个零点
有两个零点 .
.
(1)求实数a的取值范围;
(2)求证: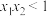 ;
;
 有两个零点
有两个零点 .
.(1)求实数a的取值范围;
(2)求证:
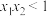 ;
;
您最近一年使用:0次
3 . 已知函数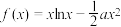 ,
, .
.
(1)求函数 的极值点个数;
的极值点个数;
(2)若函数 存在极大值点
存在极大值点 ,且使得
,且使得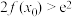 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
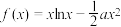 ,
, .
.(1)求函数
 的极值点个数;
的极值点个数;(2)若函数
 存在极大值点
存在极大值点 ,且使得
,且使得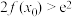 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 若至少由两个元素构成的有限集合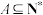 ,且对于任意的
,且对于任意的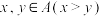 ,都有
,都有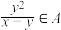 ,则称
,则称 为“
为“ 集合”.
集合”.
(1)判断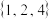 是否为“
是否为“ 集合”,说明理由;
集合”,说明理由;
(2)若双元素集 为“
为“ 集合”,且
集合”,且 ,求所有满足条件的集合
,求所有满足条件的集合 ;
;
(3)求所有满足条件的“ 集合”.
集合”.
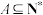 ,且对于任意的
,且对于任意的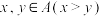 ,都有
,都有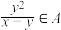 ,则称
,则称 为“
为“ 集合”.
集合”.(1)判断
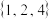 是否为“
是否为“ 集合”,说明理由;
集合”,说明理由;(2)若双元素集
 为“
为“ 集合”,且
集合”,且 ,求所有满足条件的集合
,求所有满足条件的集合 ;
;(3)求所有满足条件的“
 集合”.
集合”.
您最近一年使用:0次
昨日更新
|
251次组卷
|
4卷引用:安徽省合肥市第四中学2025届高三上学期教学诊断检测(三)数学试题
名校
解题方法
5 . 对于函数 ,定义域
,定义域 ,为若存在实数
,为若存在实数 ,使
,使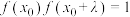 ,其中
,其中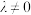 ,则称
,则称 为“倒数函数”,
为“倒数函数”, 为“
为“ 的
的 倒数点”.已知
倒数点”.已知 .
.
(1)如果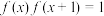 对
对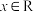 成立.求证:
成立.求证: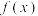 为周期函数;
为周期函数;
(2)若 为“
为“ 的
的 倒数点”,且
倒数点”,且 只有两个不同的解,求函数
只有两个不同的解,求函数 的值;
的值;
(3)设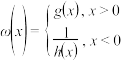 ,若函数
,若函数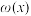 恰有3个“
恰有3个“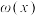 的1倒数点”,求
的1倒数点”,求 的取值范围.
的取值范围.
 ,定义域
,定义域 ,为若存在实数
,为若存在实数 ,使
,使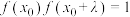 ,其中
,其中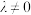 ,则称
,则称 为“倒数函数”,
为“倒数函数”, 为“
为“ 的
的 倒数点”.已知
倒数点”.已知 .
.(1)如果
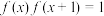 对
对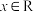 成立.求证:
成立.求证: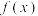 为周期函数;
为周期函数;(2)若
 为“
为“ 的
的 倒数点”,且
倒数点”,且 只有两个不同的解,求函数
只有两个不同的解,求函数 的值;
的值;(3)设
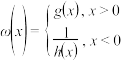 ,若函数
,若函数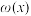 恰有3个“
恰有3个“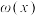 的1倒数点”,求
的1倒数点”,求 的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
208次组卷
|
2卷引用:安徽省合肥市第七中学2025届高三上学期第四次统一作业数学试题
名校
6 . 已知函数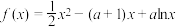 .
.
(1)讨论 的单调性;
的单调性;
(2)若函数 有极小值,且极小值大于
有极小值,且极小值大于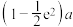 ,求实数
,求实数 的取值范围.
的取值范围.
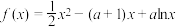 .
.(1)讨论
 的单调性;
的单调性;(2)若函数
 有极小值,且极小值大于
有极小值,且极小值大于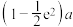 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
255次组卷
|
2卷引用:安徽省合肥市第七中学2025届高三上学期第四次统一作业数学试题
名校
解题方法
7 . 已知方程
(1)若 ,
, ,求方程
,求方程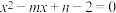 的解;
的解;
(2)若对任意实数 ,方程
,方程 恒有两个不相等的实数解,求实数
恒有两个不相等的实数解,求实数 的取值范围;
的取值范围;
(3)若方程 有两个不相等的实数解
有两个不相等的实数解 ,且
,且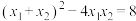 ,求
,求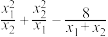 的最小值.
的最小值.

(1)若
 ,
, ,求方程
,求方程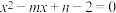 的解;
的解;(2)若对任意实数
 ,方程
,方程 恒有两个不相等的实数解,求实数
恒有两个不相等的实数解,求实数 的取值范围;
的取值范围;(3)若方程
 有两个不相等的实数解
有两个不相等的实数解 ,且
,且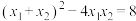 ,求
,求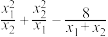 的最小值.
的最小值.
您最近一年使用:0次
7日内更新
|
849次组卷
|
3卷引用:安徽省合肥市部分学校2024—2025学年高一上学期第二次教学质量检测数学试题
名校
解题方法
8 . 已知函数 .
.
(1)若 ,
, ,函数的最小值为0,求a的值;
,函数的最小值为0,求a的值;
(2)若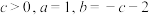 ,不等式
,不等式 有且仅有四个整数解,求实数
有且仅有四个整数解,求实数 的取值范围;
的取值范围;
(3)当 时,对
时,对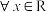 ,
,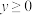 ,若存在实数m使得
,若存在实数m使得 成立,求m的最小值.
成立,求m的最小值.
 .
.(1)若
 ,
, ,函数的最小值为0,求a的值;
,函数的最小值为0,求a的值;(2)若
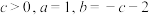 ,不等式
,不等式 有且仅有四个整数解,求实数
有且仅有四个整数解,求实数 的取值范围;
的取值范围;(3)当
 时,对
时,对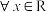 ,
,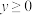 ,若存在实数m使得
,若存在实数m使得 成立,求m的最小值.
成立,求m的最小值.
您最近一年使用:0次
7日内更新
|
141次组卷
|
2卷引用:安徽省合肥市部分学校2024—2025学年高一上学期第二次教学质量检测数学试题
名校
9 . 已知集合A为非空数集,对于集合A,定义对A中任意两个不同元素相加得到一个绝对值,将这些绝对值重新组成一个新的集合,对于这一过程,我们定义为“自相加”,重新组成的集合叫做“集合A的1次自相加集合”,再次进行n-1次“自相加”操作,组成的集合叫做“集合A的n次自相加集合”,若集合A的任意k次自相加集合都不相等,则称集合A为“完美自相加集合”,同理,我们可以定义出“A的1次自相减集合”,集合A的1次自相加集合和1次自相减集合分别可表示为: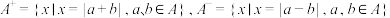 .
.
(1)已知有两个集合,集合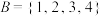 ,集合
,集合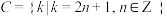 ,判断集合B和集合C是否是完美自相加集合并说明理由;
,判断集合B和集合C是否是完美自相加集合并说明理由;
(2)对(1)中的集合B进行11次自相加操作后,求:集合B的11次自相加集合的元素个数;
(3)若 且
且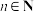 ,集合
,集合 ,
,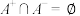 ,求:
,求: 的最小值.
的最小值.
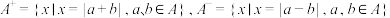 .
.(1)已知有两个集合,集合
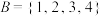 ,集合
,集合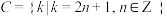 ,判断集合B和集合C是否是完美自相加集合并说明理由;
,判断集合B和集合C是否是完美自相加集合并说明理由;(2)对(1)中的集合B进行11次自相加操作后,求:集合B的11次自相加集合的元素个数;
(3)若
 且
且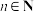 ,集合
,集合 ,
,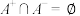 ,求:
,求: 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
10 . 设函数 .
.
(1)若不等式 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;
(2)当 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;
(3)对于任意的 ,不等式
,不等式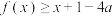 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若不等式
 的解集为
的解集为 ,求
,求 的取值范围;
的取值范围;(2)当
 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;(3)对于任意的
 ,不等式
,不等式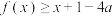 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
7日内更新
|
593次组卷
|
2卷引用:安徽省合肥市合肥一六八中学2024-2025学年高一上学期第二次月考数学试题



