名校
解题方法
1 . 高斯是德国著名的数学家,享有“数学王子”的称号,人们把函数 ,
, 称为高斯函数(其中
称为高斯函数(其中 表示不超过x的最大整数,例如:
表示不超过x的最大整数,例如: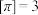 ,
,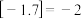 ).已知数列
).已知数列 的首项
的首项 ,前n项和记为
,前n项和记为 .若k为函数
.若k为函数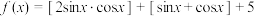 ,
, 值域内的任意元素,且当整数
值域内的任意元素,且当整数 时,都有
时,都有 成立,则
成立,则 的通项公式为
的通项公式为______ .
 ,
, 称为高斯函数(其中
称为高斯函数(其中 表示不超过x的最大整数,例如:
表示不超过x的最大整数,例如: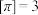 ,
,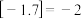 ).已知数列
).已知数列 的首项
的首项 ,前n项和记为
,前n项和记为 .若k为函数
.若k为函数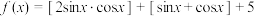 ,
, 值域内的任意元素,且当整数
值域内的任意元素,且当整数 时,都有
时,都有 成立,则
成立,则 的通项公式为
的通项公式为
您最近一年使用:0次
2 . 已知数列 满足
满足 ,
,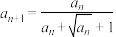 (其中
(其中 )
)
(1)判断并证明数列 的单调性;
的单调性;
(2)记数列 的前n项和为
的前n项和为 ,证明:
,证明: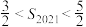 .
.
 满足
满足 ,
,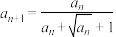 (其中
(其中 )
)(1)判断并证明数列
 的单调性;
的单调性;(2)记数列
 的前n项和为
的前n项和为 ,证明:
,证明: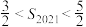 .
.
您最近一年使用:0次
2022-07-10更新
|
2211次组卷
|
5卷引用:四川省成都市第七中学2021-2022学年高一下学期期末数学试题
四川省成都市第七中学2021-2022学年高一下学期期末数学试题湖北省九校教研协作体2023届高三上学期起点考试数学试题(已下线)专题05 数列放缩(精讲精练)-2(已下线)专题10 数列通项公式的求法 微点2 累加法(已下线)专题10 数列不等式的放缩问题 (练习)
3 . 在 中,
中, ,
, ,O是
,O是 的外心,若
的外心,若 的最大值是m,数列
的最大值是m,数列 中,
中, ,
,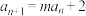 ,则
,则 的通项公式为
的通项公式为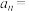 ( )
( )
 中,
中, ,
, ,O是
,O是 的外心,若
的外心,若 的最大值是m,数列
的最大值是m,数列 中,
中, ,
,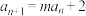 ,则
,则 的通项公式为
的通项公式为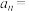 ( )
( )A. | B.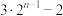 | C. | D.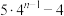 |
您最近一年使用:0次
4 . 已知在每一项均不为0的数列 中,
中, ,且
,且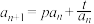 (
( 、
、 为常数,
为常数, ),记数列
),记数列 的前
的前 项和为
项和为 .
.
(1)当 时,求
时,求 ;
;
(2)当 、
、 时,
时,
①求证:数列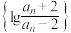 为等比数列;
为等比数列;
②是否存在正整数 ,使得不等式
,使得不等式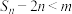 对任意
对任意 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
 中,
中, ,且
,且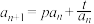 (
( 、
、 为常数,
为常数, ),记数列
),记数列 的前
的前 项和为
项和为 .
.(1)当
 时,求
时,求 ;
;(2)当
 、
、 时,
时,①求证:数列
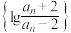 为等比数列;
为等比数列;②是否存在正整数
 ,使得不等式
,使得不等式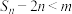 对任意
对任意 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
您最近一年使用:0次
2020-07-28更新
|
1210次组卷
|
4卷引用:四川省成都外国语学校2020-2021学年高一下学期期中数学(理科)试题
解题方法
5 . 已知数列 是首项为4,公差为2的等差数列,其前n项和为
是首项为4,公差为2的等差数列,其前n项和为 ,数列
,数列 满足
满足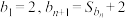 ,记
,记 表示不超过x的最大整数,如
表示不超过x的最大整数,如 .如果关于x的不等式
.如果关于x的不等式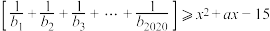 ,对任意的
,对任意的 都成立,则实数x的取值范围为( )
都成立,则实数x的取值范围为( )
 是首项为4,公差为2的等差数列,其前n项和为
是首项为4,公差为2的等差数列,其前n项和为 ,数列
,数列 满足
满足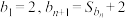 ,记
,记 表示不超过x的最大整数,如
表示不超过x的最大整数,如 .如果关于x的不等式
.如果关于x的不等式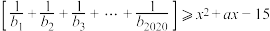 ,对任意的
,对任意的 都成立,则实数x的取值范围为( )
都成立,则实数x的取值范围为( )A. | B.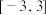 |
C.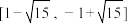 | D.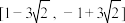 |
您最近一年使用:0次
名校
解题方法
6 . 设数列 的前
的前 项和为
项和为 ,
,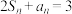 ,
, ,数列
,数列 满足:对于任意的
满足:对于任意的 ,都有
,都有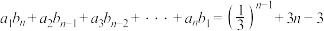 成立.
成立.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)设数列 ,问:数列
,问:数列 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
 的前
的前 项和为
项和为 ,
,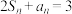 ,
, ,数列
,数列 满足:对于任意的
满足:对于任意的 ,都有
,都有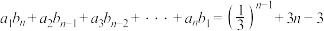 成立.
成立.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的通项公式;
的通项公式;(3)设数列
 ,问:数列
,问:数列 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
您最近一年使用:0次
2020-08-07更新
|
2004次组卷
|
11卷引用:四川省成都市石室佳兴外国语学校2019-2020学年高一下学期期中数学试题
四川省成都市石室佳兴外国语学校2019-2020学年高一下学期期中数学试题【全国市级联考】江苏省苏州市2017-2018学年高一下学期期末考试数学试题湖南省长沙市宁乡一中2019-2020年高一下学期5月月考数学试题上海市交大附中2019-2020学年高一下学期期末数学试题【全国百强校】江苏省海安高级中学2019届高三上学期第二次月考数学试题江苏省南通市海安高级中学2019-2020学年高三下学期3月线上考试数学试题江苏省泰州中学2019-2020学年高三下学期4月质量检测数学试题湖南省衡阳市第八中学2019-2020学年高二下学期6月第三次月考数学试题(已下线)专题10 数列通项公式的求法 微点1 观察法(不完全归纳法)、公式法辽宁省鞍山市第一中学2023-2024学年高二下学期第三次月考数学试题辽宁省辽宁省七校协作体2023-2024学年高二下学期5月期中数学试题
名校
解题方法
7 . 给出下列五个命题,其中正确的命题序号是________ .
①当 时,函数
时,函数 取得最大值,则
取得最大值,则
②已知菱形 ,
, 为
为 的中点,且
的中点,且 ,则菱形
,则菱形 面积的最大值为12
面积的最大值为12
③已知二次函数 ,如果
,如果 时
时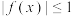 ,则实数
,则实数 的取值范围是
的取值范围是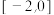
④在三棱锥 中,
中, ,
, ,点
,点 分别是
分别是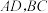 的中点,则异面直线
的中点,则异面直线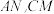 所成的角的余弦值是
所成的角的余弦值是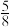
⑤数列 满足
满足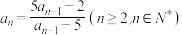 ,且数列
,且数列 的前2010项的和为403,记数列
的前2010项的和为403,记数列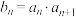 ,
, 是数列
是数列 的前
的前 项和,则
项和,则
①当
 时,函数
时,函数 取得最大值,则
取得最大值,则
②已知菱形
 ,
, 为
为 的中点,且
的中点,且 ,则菱形
,则菱形 面积的最大值为12
面积的最大值为12③已知二次函数
 ,如果
,如果 时
时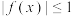 ,则实数
,则实数 的取值范围是
的取值范围是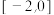
④在三棱锥
 中,
中, ,
, ,点
,点 分别是
分别是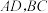 的中点,则异面直线
的中点,则异面直线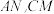 所成的角的余弦值是
所成的角的余弦值是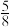
⑤数列
 满足
满足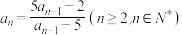 ,且数列
,且数列 的前2010项的和为403,记数列
的前2010项的和为403,记数列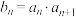 ,
, 是数列
是数列 的前
的前 项和,则
项和,则
您最近一年使用:0次
名校
解题方法
8 . 若数列 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有 成立,则称数列
成立,则称数列 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列 满足
满足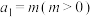 ,
,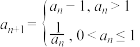 ,则下列结论中错误的是( )
,则下列结论中错误的是( )
 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有 成立,则称数列
成立,则称数列 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列 满足
满足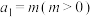 ,
,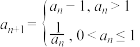 ,则下列结论中错误的是( )
,则下列结论中错误的是( )A.若 ,则m可以取3个不同的值; ,则m可以取3个不同的值; |
B.若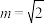 ,则数列 ,则数列 是周期为3的数列; 是周期为3的数列; |
C.对于任意的 且T≥2,存在 且T≥2,存在 ,使得 ,使得 是周期为 是周期为 的数列 的数列 |
D.存在 且 且 ,使得数列 ,使得数列 是周期数列 是周期数列 |
您最近一年使用:0次
2020-07-11更新
|
1158次组卷
|
5卷引用:四川省成都市温江区2019-2020学年度高一下学期期末考试数学试题
四川省成都市温江区2019-2020学年度高一下学期期末考试数学试题2015届湖南省长望浏宁四县高三3月调研(一模)考试理科数学试卷(已下线)专题6-1 数列函数性质与不等式放缩(讲+练)-1(已下线)专题9 周期数列 微点2 周期数列的“脸谱”识别北京一零一中学2024届高三上学期统考一数学试题
名校
解题方法
9 . 已知数列 的通项公式为
的通项公式为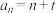 ,数列
,数列 为公比小于1的等比数列,且满足
为公比小于1的等比数列,且满足 ,
,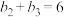 ,设
,设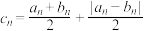 ,在数列
,在数列 中,若
中,若 ,则实数
,则实数 的取值范围为
的取值范围为
__________ .
 的通项公式为
的通项公式为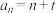 ,数列
,数列 为公比小于1的等比数列,且满足
为公比小于1的等比数列,且满足 ,
,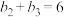 ,设
,设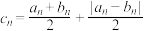 ,在数列
,在数列 中,若
中,若 ,则实数
,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
2018-04-25更新
|
2772次组卷
|
8卷引用:四川省珙县中学校2020-2021学年高一下期数学第5月月考测试题
四川省珙县中学校2020-2021学年高一下期数学第5月月考测试题江西省抚州市临川区第一中学2017-2018学年高一下学期期末数学试题河北省2018年普通高等学校招生全国统一考试模拟考试(五)调研卷理科数学试题(已下线)专题06 数列(文理)福建师范大学附属中学2023届高三上学期12月月考数学试题广东省广州市华南师范大学附属中学2023届高三上学期11月月考(二)数学试题河南省信阳市2023-2024学年高三上学期第二次教学质量检测数学试卷(已下线)河南省信阳市2023-2024学年高三上学期第二次教学质量检测数学试题变式题11-16
10 . 已知数列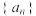 满足
满足 ,
,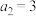 ,
,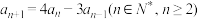 ,又
,又 .
.
(Ⅰ)求证数列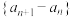 是等比数列,并求出
是等比数列,并求出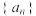 的通项公式;
的通项公式;
(Ⅱ)若 的前
的前 和为
和为 ,
,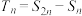 .
.
①判断并证明数列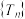 的单调性;
的单调性;
②求证: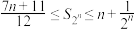
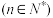 .
.
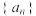 满足
满足 ,
,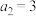 ,
,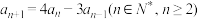 ,又
,又 .
.(Ⅰ)求证数列
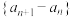 是等比数列,并求出
是等比数列,并求出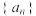 的通项公式;
的通项公式;(Ⅱ)若
 的前
的前 和为
和为 ,
,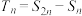 .
.①判断并证明数列
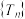 的单调性;
的单调性;②求证:
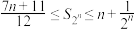
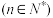 .
.
您最近一年使用:0次



