名校
1 . e是自然对数的底数, ,已知
,已知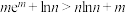 ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )
 ,已知
,已知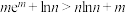 ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )A.若 ,则 ,则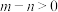 | B.若 ,则 ,则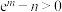 |
C.若 ,则 ,则 | D.若 ,则 ,则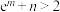 |
您最近一年使用:0次
2023-02-12更新
|
4071次组卷
|
12卷引用:【课后练】专题6 导数中的同构问题 课后作业-湘教版(2019)选择性必修第二册 第1章 导数及其应用
【课后练】专题6 导数中的同构问题 课后作业-湘教版(2019)选择性必修第二册 第1章 导数及其应用广东省茂名市2023届高三一模数学试题湖南省湘潭市部分学校2022-2023学年高三上学期期末线上联考数学试题(已下线)模块八 专题3 以函数性质与不等式为背景的压轴小题(已下线)山东省日照市2023届高三一模考试数学试题变式题11-16(已下线)专题七 导数-1专题05导数及其应用(选择题)江苏省镇江中学2023届高三下学期4月(二模)模拟数学试题(已下线)拓展六:导数的同构问题6种考法总结-【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第二册)广东省中山市桂山中学2024届高三上学期第一次月考数学试题河北省唐山市开滦第二中学2022-2023学年高二下学期3月月考数学试题(已下线)模块三 大招3 同构思想
名校
解题方法
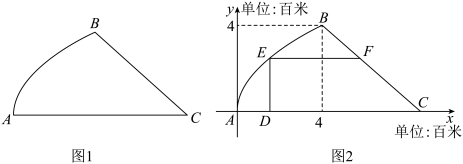
2 . 从商业化书店到公益性城市书房,再到“会呼吸的文化森林”——图书馆,建设高水平、现代化、开放式的图书馆一直以来是大众的共同心声.现有一块不规则的地,其平面图形如图1所示,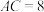 (百米),建立如图2所示的平面直角坐标系,将曲线
(百米),建立如图2所示的平面直角坐标系,将曲线 看成函数
看成函数 图象的一部分,
图象的一部分, 为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形
为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形 (如图2),则图书馆占地面积(万平方米)的最大值为( )
(如图2),则图书馆占地面积(万平方米)的最大值为( )
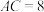 (百米),建立如图2所示的平面直角坐标系,将曲线
(百米),建立如图2所示的平面直角坐标系,将曲线 看成函数
看成函数 图象的一部分,
图象的一部分, 为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形
为一次函数图象的一部分,若在此地块上建立一座图书馆,平面图为直角梯形 (如图2),则图书馆占地面积(万平方米)的最大值为( )
(如图2),则图书馆占地面积(万平方米)的最大值为( )
A. | B.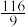 | C.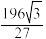 | D.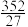 |
您最近一年使用:0次
2023-02-08更新
|
1326次组卷
|
10卷引用:1.3.4 导数的应用举例(同步练习)2022-2023学年高二选择性必修第二册素养提升检测(提高篇)
(已下线)1.3.4 导数的应用举例(同步练习)2022-2023学年高二选择性必修第二册素养提升检测(提高篇)广东省清远市清新区部分学校2023届高三下学期2月联考数学试题广东省韶关市部分学校2023届高三下学期开学考试数学试题湖南省部分学校2023届高三下学期2月联考数学试题辽宁省名校联盟2022-2023学年高三下学期质量检测考试数学试题内蒙2023届古高三仿真模拟考试理科数学试题广东省金太阳2023届高三联考数学试题湖南省湘潭钢铁集团有限公司第一子弟中学2023届高三下学期入学考试数学试题江西省贵溪市实验中学2023届高三第四次月考数学(文)试题陕西省西安市第三十八中学2023届高三2月模拟理科数学试题
3 . 设 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为“取整函数”,如:
称为“取整函数”,如: ,
, .现有关于“取整函数”的两个命题:①集合
.现有关于“取整函数”的两个命题:①集合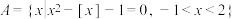 是单元素集:②对于任意
是单元素集:②对于任意 ,
,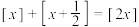 成立,则以下说法正确的是 ( )
成立,则以下说法正确的是 ( )
 ,用
,用 表示不超过
表示不超过 的最大整数,则
的最大整数,则 称为“取整函数”,如:
称为“取整函数”,如: ,
, .现有关于“取整函数”的两个命题:①集合
.现有关于“取整函数”的两个命题:①集合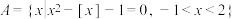 是单元素集:②对于任意
是单元素集:②对于任意 ,
,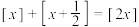 成立,则以下说法正确的是 ( )
成立,则以下说法正确的是 ( )| A.①②都是真命题 | B.①是真命题②是假命题 |
| C.①是假命题②是真命题 | D.①②都是假命题 |
您最近一年使用:0次
2024-01-15更新
|
1119次组卷
|
6卷引用:1.5.1 全称量词与存在量词——课后作业(提升版)
(已下线)1.5.1 全称量词与存在量词——课后作业(提升版)上海市松江区2023-2024学年高一上学期期末质量监控数学试卷 (已下线)第05讲 全称量词与存在量词-【暑假预科讲义】(人教A版2019必修第一册)(已下线)专题02 常用逻辑用语-【暑假自学课】(沪教版2020必修第一册)上海市上海交通大学附属中学2024-2025学年高一上学期9月数学练习卷安徽省宣城市第二中学2024-2025学年高一上学期第一次调研测试(10月)数学试题
名校
解题方法
4 . 已知函数 ,
,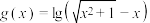 ,则( )
,则( )
 ,
,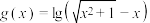 ,则( )
,则( )A.函数 为偶函数 为偶函数 |
B.函数 为奇函数 为奇函数 |
C.函数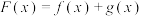 在区间 在区间 上的最大值与最小值之和为0 上的最大值与最小值之和为0 |
D.设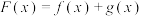 ,则 ,则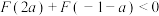 的解集为 的解集为 |
您最近一年使用:0次
2021-08-02更新
|
4002次组卷
|
14卷引用:试卷18(第1章-6.3 对数函数)-2021-2022学年高一数学易错题、精典题滚动训练(苏教版2019必修第一册)
(已下线)试卷18(第1章-6.3 对数函数)-2021-2022学年高一数学易错题、精典题滚动训练(苏教版2019必修第一册)(已下线)试卷19(第1章-6.4 指数函数与对数函数综合)-2021-2022学年高一数学易错题、精典题滚动训练(苏教版2019必修第一册)山东省烟台市2020-2021学年高二下学期期末数学试题江苏省南京市第五中学2021-2022学年高三上学期一模热身数学试题(已下线)课时4.4.1(同步练习)对数函数-2021-2022学年高一数学新课学习讲与练精品资源(人教版2019必修第一册)江苏省徐州市第三十六中学2021-2022学年高一上学期12月月考数学试题山东省滨州市阳信县2021-2022学年高二下学期期中考试数学试题苏教版(2019) 必修第一册 突围者 第6章 全章综合检测江西省上饶市广丰区重点高中2022-2023学年高一上学期第三次月考数学试题辽宁省沈阳市铁路实验中学2022-2023学年高一上学期12月月考数学试题湖南省衡阳市第八中学2022-2023学年高一上学期期末数学试题陕西省西安高新唐南中学2022-2023学年高一上学期期末数学试题(已下线)6.3 对数函数-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)湖北省恩施州高中教育联盟2022-2023学年高一下学期期中数学试题
解题方法
5 . 2024年1月,某市的高二调研考试首次采用了“ ”新高考模式.该模式下,计算学生个人总成绩时,“
”新高考模式.该模式下,计算学生个人总成绩时,“ ”的学科均以原始分记入,再选的“2”个学科(学生在政治、地理、化学、生物中选修的2科)以赋分成绩记入.赋分成绩的具体算法是:先将该市某再选科目原始成绩按从高到低划分为
”的学科均以原始分记入,再选的“2”个学科(学生在政治、地理、化学、生物中选修的2科)以赋分成绩记入.赋分成绩的具体算法是:先将该市某再选科目原始成绩按从高到低划分为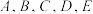 五个等级,各等级人数所占比例分别约为
五个等级,各等级人数所占比例分别约为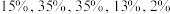 .依照转换公式,将五个等级的原始分分别转换到
.依照转换公式,将五个等级的原始分分别转换到 五个分数区间,并对所得分数的小数点后一位进行“四舍五入”,最后得到保留为整数的转换分成绩,并作为赋分成绩.具体等级比例和赋分区间如下表:
五个分数区间,并对所得分数的小数点后一位进行“四舍五入”,最后得到保留为整数的转换分成绩,并作为赋分成绩.具体等级比例和赋分区间如下表:
已知该市本次高二调研考试化学科目考试满分为100分.
(2)现从该市本次高二调研考试的化学成绩中随机选取100名学生的原始成绩进行分析,其频率分布直方图如图所示,求出图中 的值,并用样本估计总体的方法,估计该市本次化学原始成绩
的值,并用样本估计总体的方法,估计该市本次化学原始成绩 等级中的最低分.
等级中的最低分.
 ”新高考模式.该模式下,计算学生个人总成绩时,“
”新高考模式.该模式下,计算学生个人总成绩时,“ ”的学科均以原始分记入,再选的“2”个学科(学生在政治、地理、化学、生物中选修的2科)以赋分成绩记入.赋分成绩的具体算法是:先将该市某再选科目原始成绩按从高到低划分为
”的学科均以原始分记入,再选的“2”个学科(学生在政治、地理、化学、生物中选修的2科)以赋分成绩记入.赋分成绩的具体算法是:先将该市某再选科目原始成绩按从高到低划分为 五个等级,各等级人数所占比例分别约为
五个等级,各等级人数所占比例分别约为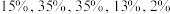 .依照转换公式,将五个等级的原始分分别转换到
.依照转换公式,将五个等级的原始分分别转换到 五个分数区间,并对所得分数的小数点后一位进行“四舍五入”,最后得到保留为整数的转换分成绩,并作为赋分成绩.具体等级比例和赋分区间如下表:
五个分数区间,并对所得分数的小数点后一位进行“四舍五入”,最后得到保留为整数的转换分成绩,并作为赋分成绩.具体等级比例和赋分区间如下表:| 等级 |  | 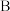 | 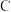 | 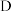 |  |
| 比例 |  |  |  | 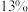 |  |
| 赋分区间 | 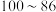 |  | 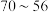 |  |  |

(2)现从该市本次高二调研考试的化学成绩中随机选取100名学生的原始成绩进行分析,其频率分布直方图如图所示,求出图中
 的值,并用样本估计总体的方法,估计该市本次化学原始成绩
的值,并用样本估计总体的方法,估计该市本次化学原始成绩 等级中的最低分.
等级中的最低分.
您最近一年使用:0次
2024-03-21更新
|
861次组卷
|
8卷引用:9.2.1?总体取值规律的估计——课后作业(提升版)
(已下线)9.2.1?总体取值规律的估计——课后作业(提升版)四川省成都市2024届高三下学期第二次诊断性检测文科数学试题(已下线)专题9.5 统计全章八大压轴题型归纳(拔尖篇)--举一反三系列(人教A版2019必修第二册)(已下线)专题9.3 统计图的相关运算大题专项训练-举一反三系列(人教A版2019必修第二册)(已下线)第14章 统计(提升卷)-重难点突破及混淆易错规避(苏教版2019必修第二册)(已下线)14.4 用样本估计总体(2)-【帮课堂】(苏教版2019必修第二册)(已下线)专题05 第九章 统计-期末考点大串讲(人教A版2019必修第二册)(已下线)第四章 统计 专题一 用样本估计总体 微点2 用样本估计总体(二)【培优版】
名校
解题方法
6 . 在复习了函数性质后,某同学发现:函数 为奇函数的充要条件是
为奇函数的充要条件是 的图彖关于坐标原点成中心对称:可以引申为:函数
的图彖关于坐标原点成中心对称:可以引申为:函数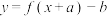 为奇函数,则
为奇函数,则 图象关于点
图象关于点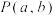 成中心对称.现在已知函数
成中心对称.现在已知函数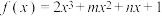 的图象关于
的图象关于 成中心对称,则下列结论正确的是( )
成中心对称,则下列结论正确的是( )
 为奇函数的充要条件是
为奇函数的充要条件是 的图彖关于坐标原点成中心对称:可以引申为:函数
的图彖关于坐标原点成中心对称:可以引申为:函数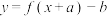 为奇函数,则
为奇函数,则 图象关于点
图象关于点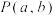 成中心对称.现在已知函数
成中心对称.现在已知函数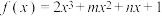 的图象关于
的图象关于 成中心对称,则下列结论正确的是( )
成中心对称,则下列结论正确的是( )A. |
B. |
C. |
D.对任意 ,都有 ,都有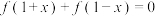 |
您最近一年使用:0次
2022-08-01更新
|
1517次组卷
|
9卷引用:突破3.2 函数的基本性质(2)
解题方法
7 . 某微生物科研团队为了研究某种细菌的繁殖情况,工作人员配制了一种适合该细菌繁殖的营养基质用以培养该细菌,通过相关设备以及分析计算后得到:该细菌在前3个小时的细菌数 与时间
与时间 (单位:小时,且
(单位:小时,且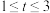 )满足回归方程
)满足回归方程 (其中
(其中 为常数),若
为常数),若 ,且前3个小时
,且前3个小时 与
与 的部分数据如下表:
的部分数据如下表:
3个小时后,向该营养基质中加入某种细菌抑制剂,分析计算后得到细菌数 与时间
与时间 (单位:小时,且
(单位:小时,且 )满足关系式:
)满足关系式: ,在
,在 时刻,该细菌数达到最大,随后细菌个数逐渐减少,则
时刻,该细菌数达到最大,随后细菌个数逐渐减少,则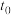 的值为( )
的值为( )
 与时间
与时间 (单位:小时,且
(单位:小时,且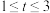 )满足回归方程
)满足回归方程 (其中
(其中 为常数),若
为常数),若 ,且前3个小时
,且前3个小时 与
与 的部分数据如下表:
的部分数据如下表:
| 1 | 2 | 3 |
|
|
|
|
 与时间
与时间 (单位:小时,且
(单位:小时,且 )满足关系式:
)满足关系式: ,在
,在 时刻,该细菌数达到最大,随后细菌个数逐渐减少,则
时刻,该细菌数达到最大,随后细菌个数逐渐减少,则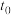 的值为( )
的值为( )| A.4 | B. | C.5 | D.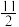 |
您最近一年使用:0次
2022-10-03更新
|
1321次组卷
|
10卷引用:9.1.2线性回归方程(2)
(已下线)9.1.2线性回归方程(2)(已下线)8.2一元线性回归分析(分层练习)-2022-2023学年高二数学同步精品课堂(沪教版2020选择性必修第二册)2023届新高考Ⅰ卷第二次统一调研模拟考试数学试题(已下线)专题21 概率与成对数据的统计分析(模拟练)(已下线)第01讲 统计(练)(已下线)模块三 专题3 小题满分挑战练( 2)(北师大2019版 高二)(已下线)模块三 专题3 小题满分挑战练( 2)(苏教版高二)(已下线)第9章:统计 章末检测试卷(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)第四章 统计 专题二 统计相关性与回归分析 微点4 相关分析与回归分析综合训练【培优版】
名校
解题方法
8 . 经过市场调研发现,某公司生产的某种时令商品在未来一个月(30天)内的日销售量 (百件)与时间第
(百件)与时间第 天的关系如下表所示:
天的关系如下表所示:
未来30天内,受市场因素影响,前15天此商品每天每件的利润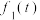 (元)与时间第
(元)与时间第 天的函数关系式为
天的函数关系式为 ,且
,且 为整数
为整数 ,而后15天此商品每天每件的利润
,而后15天此商品每天每件的利润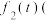 元
元 与时间第
与时间第 天的函数关系式为
天的函数关系式为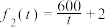 (
(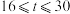 ,且
,且 为整数).
为整数).
(1)现给出以下两类函数模型:① (
(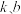 为常数);②
为常数);②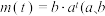 为常数,
为常数, 且
且 .分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;
.分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;
(2)若这30天内该公司此商品的日销售利润始终不能超过4万元,则考虑转型.请判断该公司是否需要转型?并说明理由.
 (百件)与时间第
(百件)与时间第 天的关系如下表所示:
天的关系如下表所示:第 天 天 | 1 | 3 | 10 |  | 30 |
日销售量 (百件) (百件) | 2 | 3 | 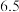 |  |  |
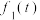 (元)与时间第
(元)与时间第 天的函数关系式为
天的函数关系式为 ,且
,且 为整数
为整数 ,而后15天此商品每天每件的利润
,而后15天此商品每天每件的利润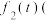 元
元 与时间第
与时间第 天的函数关系式为
天的函数关系式为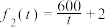 (
(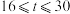 ,且
,且 为整数).
为整数).(1)现给出以下两类函数模型:①
 (
(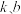 为常数);②
为常数);②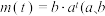 为常数,
为常数, 且
且 .分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;
.分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;(2)若这30天内该公司此商品的日销售利润始终不能超过4万元,则考虑转型.请判断该公司是否需要转型?并说明理由.
您最近一年使用:0次
2022-06-25更新
|
1267次组卷
|
10卷引用:突破3.4 函数的应用(一)(课时训练)
(已下线)突破3.4 函数的应用(一)(课时训练)上海市金山区2022届高三下学期二模数学试题河南省郑州市第七中学2022-2023学年高三上学期8月月考数学理科试题黑龙江省大庆市大庆实验中学2022-2023学年高一上学期10月月考数学试题河北省衡水中学2023届高三上学期一调数学试题宁夏石嘴山市第三中学2022-2023学年高一上学期第二次考试数学试题(已下线)2023年上海高考数学模拟卷02(已下线)3.4函数的应用(一)(分层作业)-【上好课】宁夏回族自治区银川一中2024届高三上学期第二次月考数学(理)试题【巩固卷】第5章测评卷 单元测试A-沪教版(2020)必修第一册
9 . 阅读材料:我们研究了函数的单调性、奇偶性和周期性,但是这些还不能够准确地描述出函数的图象,例如函数 和
和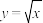 ,虽然它们都是增函数,图象在
,虽然它们都是增函数,图象在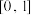 上都是上升的,但是却有着显著的不同.如图1所示,函数
上都是上升的,但是却有着显著的不同.如图1所示,函数 的图象是向下凸的,在
的图象是向下凸的,在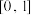 上任意取两个点
上任意取两个点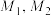 ,函数
,函数 的图象总是在线段
的图象总是在线段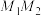 的下方,此时函数
的下方,此时函数 称为下凸函数;函数
称为下凸函数;函数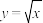 的图象是向上凸的,在
的图象是向上凸的,在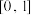 上任意取两个点
上任意取两个点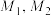 ,函数
,函数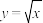 的图象总是在线段
的图象总是在线段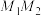 的上方,则函数
的上方,则函数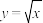 称为上凸函数.具有这样特征的函数通常称做凸函数.
称为上凸函数.具有这样特征的函数通常称做凸函数.
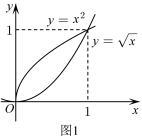
定义1:设函数 是定义在区间I上的连续函数,若
是定义在区间I上的连续函数,若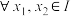 ,都有
,都有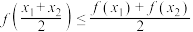 ,则称
,则称 为区间I上的下凸函数.如图2.下凸函数的形状特征:曲线上任意两点
为区间I上的下凸函数.如图2.下凸函数的形状特征:曲线上任意两点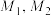 之间的部分位于线段
之间的部分位于线段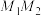 的下方.定义2:设函数
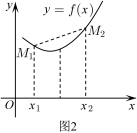
的下方.定义2:设函数 是定义在区间I上的连续函数,若
是定义在区间I上的连续函数,若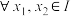 ,都有
,都有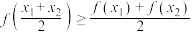 ,则称
,则称 为区间I上的上凸函数.如图3.上凸函数的形状特征:曲线上任意两点
为区间I上的上凸函数.如图3.上凸函数的形状特征:曲线上任意两点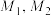 之间的部分位于线段
之间的部分位于线段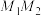 的上方.上凸(下凸)函数与函数的定义域密切相关的.例如,函数
的上方.上凸(下凸)函数与函数的定义域密切相关的.例如,函数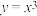 在
在 为上凸函数,在
为上凸函数,在 上为下凸函数.函数的奇偶性和周期性分别反映的是函数图象的对称性和循环往复,属于整体性质;而函数的单调性和凸性分别刻画的是函数图象的升降和弯曲方向,属于局部性质.关于函数性质的探索,对我们的启示是:在认识事物和研究问题时,只有从多角度、全方位加以考查,才能使认识和研究更加准确.结合阅读材料回答下面的问题:
上为下凸函数.函数的奇偶性和周期性分别反映的是函数图象的对称性和循环往复,属于整体性质;而函数的单调性和凸性分别刻画的是函数图象的升降和弯曲方向,属于局部性质.关于函数性质的探索,对我们的启示是:在认识事物和研究问题时,只有从多角度、全方位加以考查,才能使认识和研究更加准确.结合阅读材料回答下面的问题:
(1)请尝试列举一个下凸函数:___________;
(2)求证:二次函数 是上凸函数;
是上凸函数;
(3)已知函数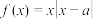 ,若对任意
,若对任意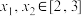 ,恒有
,恒有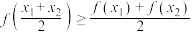 ,尝试数形结合探究实数a的取值范围.
,尝试数形结合探究实数a的取值范围.
 和
和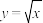 ,虽然它们都是增函数,图象在
,虽然它们都是增函数,图象在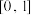 上都是上升的,但是却有着显著的不同.如图1所示,函数
上都是上升的,但是却有着显著的不同.如图1所示,函数 的图象是向下凸的,在
的图象是向下凸的,在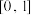 上任意取两个点
上任意取两个点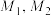 ,函数
,函数 的图象总是在线段
的图象总是在线段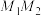 的下方,此时函数
的下方,此时函数 称为下凸函数;函数
称为下凸函数;函数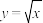 的图象是向上凸的,在
的图象是向上凸的,在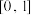 上任意取两个点
上任意取两个点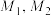 ,函数
,函数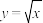 的图象总是在线段
的图象总是在线段 的上方,则函数
的上方,则函数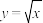 称为上凸函数.具有这样特征的函数通常称做凸函数.
称为上凸函数.具有这样特征的函数通常称做凸函数.


定义1:设函数
 是定义在区间I上的连续函数,若
是定义在区间I上的连续函数,若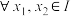 ,都有
,都有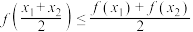 ,则称
,则称 为区间I上的下凸函数.如图2.下凸函数的形状特征:曲线上任意两点
为区间I上的下凸函数.如图2.下凸函数的形状特征:曲线上任意两点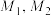 之间的部分位于线段
之间的部分位于线段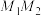 的下方.定义2:设函数
的下方.定义2:设函数 是定义在区间I上的连续函数,若
是定义在区间I上的连续函数,若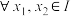 ,都有
,都有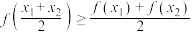 ,则称
,则称 为区间I上的上凸函数.如图3.上凸函数的形状特征:曲线上任意两点
为区间I上的上凸函数.如图3.上凸函数的形状特征:曲线上任意两点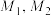 之间的部分位于线段
之间的部分位于线段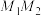 的上方.上凸(下凸)函数与函数的定义域密切相关的.例如,函数
的上方.上凸(下凸)函数与函数的定义域密切相关的.例如,函数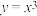 在
在 为上凸函数,在
为上凸函数,在 上为下凸函数.函数的奇偶性和周期性分别反映的是函数图象的对称性和循环往复,属于整体性质;而函数的单调性和凸性分别刻画的是函数图象的升降和弯曲方向,属于局部性质.关于函数性质的探索,对我们的启示是:在认识事物和研究问题时,只有从多角度、全方位加以考查,才能使认识和研究更加准确.结合阅读材料回答下面的问题:
上为下凸函数.函数的奇偶性和周期性分别反映的是函数图象的对称性和循环往复,属于整体性质;而函数的单调性和凸性分别刻画的是函数图象的升降和弯曲方向,属于局部性质.关于函数性质的探索,对我们的启示是:在认识事物和研究问题时,只有从多角度、全方位加以考查,才能使认识和研究更加准确.结合阅读材料回答下面的问题:(1)请尝试列举一个下凸函数:___________;
(2)求证:二次函数
 是上凸函数;
是上凸函数;(3)已知函数
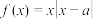 ,若对任意
,若对任意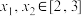 ,恒有
,恒有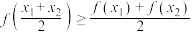 ,尝试数形结合探究实数a的取值范围.
,尝试数形结合探究实数a的取值范围.
您最近一年使用:0次
2022-03-01更新
|
1358次组卷
|
4卷引用:聚焦核心素养-一元二次函数、方程和不等式
聚焦核心素养-一元二次函数、方程和不等式贵州省贵阳市普通中学2021-2022学年高一上学期期末监测考试数学试题第三章 函数的概念与性质(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)(已下线)第一章 导数与函数的图像 专题二 函数的凹凸性与渐近线 微点2 函数的凹凸性与渐近线综合训练
名校
10 . 在① 是三次函数,且
是三次函数,且 ,
,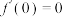 ,
,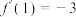 ,
,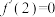 ,②
,② 是二次函数,且
是二次函数,且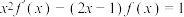 这两个条件中任选一个作为已知条件,并回答下列问题.
这两个条件中任选一个作为已知条件,并回答下列问题.
(1)求函数 的解析式;
的解析式;
(2)求 的图象在
的图象在 处的切线l与两坐标轴围成的三角形的面积.
处的切线l与两坐标轴围成的三角形的面积.
 是三次函数,且
是三次函数,且 ,
,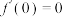 ,
,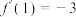 ,
,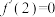 ,②
,② 是二次函数,且
是二次函数,且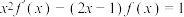 这两个条件中任选一个作为已知条件,并回答下列问题.
这两个条件中任选一个作为已知条件,并回答下列问题.(1)求函数
 的解析式;
的解析式;(2)求
 的图象在
的图象在 处的切线l与两坐标轴围成的三角形的面积.
处的切线l与两坐标轴围成的三角形的面积.
您最近一年使用:0次
2021-10-22更新
|
1713次组卷
|
12卷引用:5.2 导数的运算-2021-2022学年高二数学尖子生同步培优题典(苏教版2019选择性必修第一册)
(已下线)5.2 导数的运算-2021-2022学年高二数学尖子生同步培优题典(苏教版2019选择性必修第一册)人教B版(2019) 选修第三册 名师精选 第七单元 基本初等函数的导数、求导法则及其应用(B卷)(已下线)5.2导数的运算C卷2023版 苏教版(2019) 选修第一册 名师精选卷 第十三单元 导数的概念、导数的运算 B卷沪教版(2020) 选修第二册 经典学案 第5章 5.2导数的运算北师大版(2019) 选修第二册 名师精选 第七单元 导数的计算、导数的四则运算法则、简单复合函数的求导法则(A卷)(已下线)第04讲 导数的四则运算法则-【帮课堂】2021-2022学年高二数学同步精品讲义(人教A版2019选择性必修第二册)(已下线)卷07 导数的概念及其意义、导数的运算 A卷 ·基础达标-【重难点突破】2021-2022学年高二数学名校好题汇编同步测试卷(人教A版选择性必修第二册)(已下线)第一章 导数与函数的图像 专题四 三次函数切线问题 微点1 三次函数切线问题江苏省建湖高级中学2023-2024学年高二下学期期初测试(2月)数学试题【随堂练】 5.2 导数的运算 随堂练习-沪教版(2020)选择性必修第二册第5章 导数及其应用(已下线)函数解析式的求法