解题方法
1 . 已知函数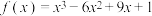 .
.
(1)求函数 在
在 处的切线方程;
处的切线方程;
(2)当 时,求函数
时,求函数 的最大值.
的最大值.
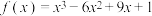 .
.(1)求函数
 在
在 处的切线方程;
处的切线方程;(2)当
 时,求函数
时,求函数 的最大值.
的最大值.
您最近一年使用:0次
2024-07-31更新
|
297次组卷
|
2卷引用:浙江省嘉兴市2023-2024学年高二下学期6月期末检测数学试题
名校
2 . 已知点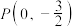 ,点
,点 在
在 轴上,点
轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在直线
在直线 上,且满足
上,且满足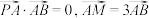 .
.
(1)当点 在
在 轴上移动时,求动点
轴上移动时,求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设 为(1)中的曲线
为(1)中的曲线 上一点,直线
上一点,直线 过点
过点 且与曲线
且与曲线 在点
在点 处的切线垂直,
处的切线垂直, 与曲线
与曲线 相交于另一点
相交于另一点 ,当
,当 (
( 为坐标原点)时,求直线
为坐标原点)时,求直线 的方程.
的方程.
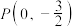 ,点
,点 在
在 轴上,点
轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在直线
在直线 上,且满足
上,且满足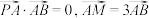 .
.(1)当点
 在
在 轴上移动时,求动点
轴上移动时,求动点 的轨迹
的轨迹 的方程;
的方程;(2)设
 为(1)中的曲线
为(1)中的曲线 上一点,直线
上一点,直线 过点
过点 且与曲线
且与曲线 在点
在点 处的切线垂直,
处的切线垂直, 与曲线
与曲线 相交于另一点
相交于另一点 ,当
,当 (
( 为坐标原点)时,求直线
为坐标原点)时,求直线 的方程.
的方程.
您最近一年使用:0次
3 . 已知函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 在区间
在区间 上的最大值
上的最大值 的表达式;
的表达式;
(3)若函数 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
 .
.(1)若
 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 在区间
在区间 上的最大值
上的最大值 的表达式;
的表达式;(3)若函数
 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
4 . 已知函数 ,下列结论正确的是( )
,下列结论正确的是( )
 ,下列结论正确的是( )
,下列结论正确的是( )A.当 时, 时, 在 在 处的切线方程为 处的切线方程为 |
B.当 时, 时,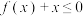 恒成立 恒成立 |
C.若 恰有一个零点,则 恰有一个零点,则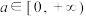 |
D.若 恰有两个零点,则 恰有两个零点,则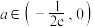 |
您最近一年使用:0次
解题方法
5 . 已知函数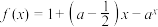 .
.
(1)当 时,求曲线
时,求曲线 在点
在点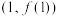 处的切线方程;
处的切线方程;
(2)当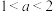 时,证明:
时,证明: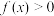 在
在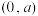 上恒成立.
上恒成立.
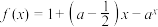 .
.(1)当
 时,求曲线
时,求曲线 在点
在点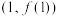 处的切线方程;
处的切线方程;(2)当
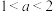 时,证明:
时,证明: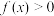 在
在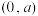 上恒成立.
上恒成立.
您最近一年使用:0次
6 . 若曲线 在点
在点 处的切线方程为
处的切线方程为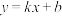 ,则
,则 的最大值为( )
的最大值为( )
 在点
在点 处的切线方程为
处的切线方程为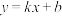 ,则
,则 的最大值为( )
的最大值为( )A. | B.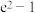 |
C. | D. |
您最近一年使用:0次
名校
7 . 关于函数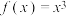 的图象的切线,下列说法正确的是( )
的图象的切线,下列说法正确的是( )
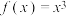 的图象的切线,下列说法正确的是( )
的图象的切线,下列说法正确的是( )A.在点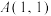 处的切线方程为 处的切线方程为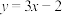 |
B.经过点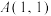 的切线方程为 的切线方程为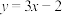 |
C.切线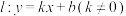 与 与 的图象必有两个公共点 的图象必有两个公共点 |
D.在点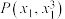 处的切线过点 处的切线过点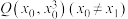 ,则 ,则 |
您最近一年使用:0次
2024-06-27更新
|
221次组卷
|
2卷引用:浙江省台州市2023-2024学年高二下学期6月期末考试数学试题
8 . 已知函数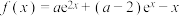 ,
, .
.
(1)当 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(2)讨论 的单调性.
的单调性.
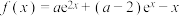 ,
, .
.(1)当
 时,求
时,求 在
在 处的切线方程;
处的切线方程;(2)讨论
 的单调性.
的单调性.
您最近一年使用:0次
9 . 已知曲线 :
: ,曲线
,曲线 :
: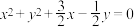 ,两曲线在第二象限交于点
,两曲线在第二象限交于点 ,
, ,
, 在
在 处的切线倾斜角分别为
处的切线倾斜角分别为 ,
, ,则( )
,则( )
 :
: ,曲线
,曲线 :
: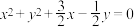 ,两曲线在第二象限交于点
,两曲线在第二象限交于点 ,
, ,
, 在
在 处的切线倾斜角分别为
处的切线倾斜角分别为 ,
, ,则( )
,则( )A.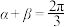 | B.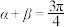 | C.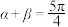 | D.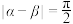 |
您最近一年使用:0次
10 . 若曲线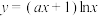 有两条过坐标原点的切线,则
有两条过坐标原点的切线,则 的取值范围是( )
的取值范围是( )
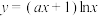 有两条过坐标原点的切线,则
有两条过坐标原点的切线,则 的取值范围是( )
的取值范围是( )A. | B.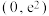 | C.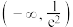 | D.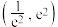 |
您最近一年使用:0次
2024-06-18更新
|
1088次组卷
|
4卷引用:浙江省衢州市2023-2024学年高二下学期6月教学质量检测数学试题
浙江省衢州市2023-2024学年高二下学期6月教学质量检测数学试题(已下线)第三章 第五节 导数与函数零点【同步课时】提升卷(已下线)专题11 切线方程 利用切点(经典好题母题)【练】福建省泉州实验中学2024-2025学年高三上学期10月月考数学试题



