解题方法
1 . 今年立秋以后,川渝地区持续性高温登上热搜,引发关注讨论.根据专家推测,主要是由于大陆高压和西太平洋副热带高压呈现非常强大,在高压的控制下,川渝地区上空晴朗少云,在太阳辐射增温和气流下沉增温的共同作用下,两个地区的气温出现了直接攀升的状态.川东北某城市一室内游泳馆,为给顾客更好的体验,推出了A和B两个套餐服务,顾客可自由选择A和B两个套餐之一;该游泳馆在App平台上推出了优惠券活动,下表是App平台统计某周内周一至周六销售优惠券情况.
经计算可得: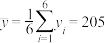 ,
,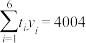 ,
,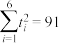 .
.
(1)因为优惠券销售火爆,App平台在周六时系统出现异常,导致当天顾客购买优惠券数量大幅减少,现剔除周六数据,求y关于t的经验回归方程;
(2)若购买优惠券的顾客选择A套餐的概率为 ,选择B套餐的概率为
,选择B套餐的概率为 ,并且A套餐包含两张优惠券,B套餐包含一张优惠券,记App平台累计销售优惠券为n张的概率为
,并且A套餐包含两张优惠券,B套餐包含一张优惠券,记App平台累计销售优惠券为n张的概率为 ,求
,求 ;
;
(3)请依据下列定义,解决下列问题:
定义:如果对于任意给定的正数 ,总存在正整数
,总存在正整数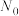 ,使得当
,使得当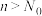 时,
时, (a是一个确定的实数),则称数列
(a是一个确定的实数),则称数列 收敛于a.
收敛于a.
运用:记(2)中所得概率 的值构成数列
的值构成数列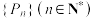 .求
.求 的最值,并证明数列
的最值,并证明数列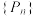 收敛.
收敛.
参考公式: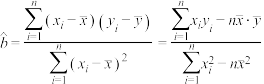 ,
, .
.
星期t | 1 | 2 | 3 | 4 | 5 | 6 |
销售量y(张) | 218 | 224 | 230 | 232 | 236 | 90 |
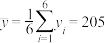 ,
,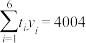 ,
,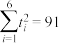 .
.(1)因为优惠券销售火爆,App平台在周六时系统出现异常,导致当天顾客购买优惠券数量大幅减少,现剔除周六数据,求y关于t的经验回归方程;
(2)若购买优惠券的顾客选择A套餐的概率为
 ,选择B套餐的概率为
,选择B套餐的概率为 ,并且A套餐包含两张优惠券,B套餐包含一张优惠券,记App平台累计销售优惠券为n张的概率为
,并且A套餐包含两张优惠券,B套餐包含一张优惠券,记App平台累计销售优惠券为n张的概率为 ,求
,求 ;
;(3)请依据下列定义,解决下列问题:
定义:如果对于任意给定的正数
 ,总存在正整数
,总存在正整数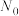 ,使得当
,使得当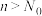 时,
时, (a是一个确定的实数),则称数列
(a是一个确定的实数),则称数列 收敛于a.
收敛于a.运用:记(2)中所得概率
 的值构成数列
的值构成数列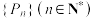 .求
.求 的最值,并证明数列
的最值,并证明数列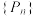 收敛.
收敛.参考公式:
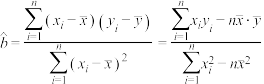 ,
, .
.
您最近一年使用:0次
名校
2 . 已知函数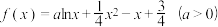
(1)判断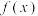 的单调性;
的单调性;
(2)若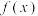 有且仅有一个零点,求
有且仅有一个零点,求 的取值范围;
的取值范围;
(3)若 取第(2)问所求范围的最小值,且数列
取第(2)问所求范围的最小值,且数列 满足,
满足, ,
,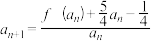 ,求证:
,求证: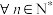 ,
,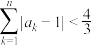 .
.
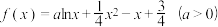
(1)判断
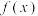 的单调性;
的单调性;(2)若
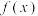 有且仅有一个零点,求
有且仅有一个零点,求 的取值范围;
的取值范围;(3)若
 取第(2)问所求范围的最小值,且数列
取第(2)问所求范围的最小值,且数列 满足,
满足, ,
,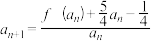 ,求证:
,求证: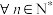 ,
,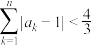 .
.
您最近一年使用:0次
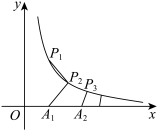
3 . 如图,已知点列 与
与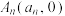 满足
满足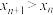 ,
,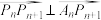 且
且 ,其中
,其中 ,
, .
. ;
;
(2)求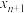 与
与 的关系式;
的关系式;
(3)证明: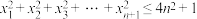 .
.
 与
与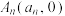 满足
满足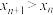 ,
,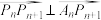 且
且 ,其中
,其中 ,
, .
.
 ;
;(2)求
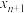 与
与 的关系式;
的关系式;(3)证明:
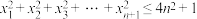 .
.
您最近一年使用:0次
2024-08-20更新
|
561次组卷
|
3卷引用:四川省新高考联盟校级2025届高三九月适应考数学试题
4 . 对于任意正整数n,进行如下操作:若n为偶数,则对n不断地除以2,直到得到一个奇数,记这个奇数为 ;若n为奇数,则对
;若n为奇数,则对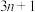 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.
(1)求20以内的质数“理想数”;
(2)已知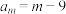 .求m的值;
.求m的值;
(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: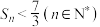 .
.
 ;若n为奇数,则对
;若n为奇数,则对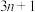 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.(1)求20以内的质数“理想数”;
(2)已知
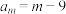 .求m的值;
.求m的值;(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列
 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: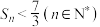 .
.
您最近一年使用:0次
2024-08-10更新
|
1107次组卷
|
8卷引用:四川省内江市威远县威远中学校2024-2025学年高三上学期9月月考数学试题
5 . 已知数列 满足
满足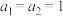 ,数列
,数列 为公差为
为公差为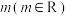 的等差数列,且满足
的等差数列,且满足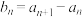 .记
.记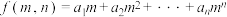 ,称
,称 为由数列
为由数列 生成的“
生成的“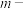 函数”.
函数”.
(1)求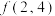 的值;
的值;
(2)若“1-函数” ,求n的最小值;
,求n的最小值;
(3)记函数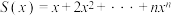 ,其导函数为
,其导函数为 ,证明:“
,证明:“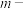 函数”
函数”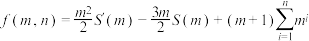 .
.
附: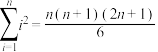
 满足
满足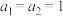 ,数列
,数列 为公差为
为公差为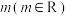 的等差数列,且满足
的等差数列,且满足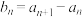 .记
.记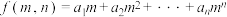 ,称
,称 为由数列
为由数列 生成的“
生成的“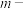 函数”.
函数”.(1)求
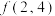 的值;
的值;(2)若“1-函数”
 ,求n的最小值;
,求n的最小值;(3)记函数
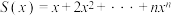 ,其导函数为
,其导函数为 ,证明:“
,证明:“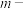 函数”
函数”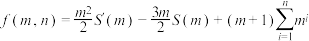 .
.附:
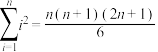
您最近一年使用:0次
2024-07-20更新
|
348次组卷
|
4卷引用:四川省德阳市高中2024-2025学年高三上学期质量监测考试(一)数学试卷
四川省德阳市高中2024-2025学年高三上学期质量监测考试(一)数学试卷山东省日照市2023-2024学年高二下学期期末考试数学试题(已下线)专题3 数列中的新定义压轴大题(过关集训)(已下线)全真综合模拟卷(四)(高三大一轮好卷)(基础卷)
解题方法
6 . 已知新同学小王每天中午会在自己学校提供的A、B两家餐厅中选择就餐,小王第1天午餐时随机选择一家餐厅用餐、如果第1天去A餐厅,那么第2天去A餐厅的概率为0.8;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.4,如此往复.
(1)求小王第2天中午去A餐厅用餐的概率;
(2)求小王第i天中午去B餐厅用餐的概率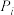 ;
;
(3)已知:若随机变量 服从两点分布,且
服从两点分布,且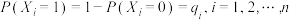 ,则
,则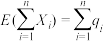 .记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求
.记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求 .
.
(1)求小王第2天中午去A餐厅用餐的概率;
(2)求小王第i天中午去B餐厅用餐的概率
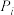 ;
;(3)已知:若随机变量
 服从两点分布,且
服从两点分布,且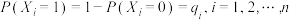 ,则
,则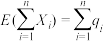 .记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求
.记前n次(即从第1次到第n次午餐)中小王去B餐厅用午餐的次数为Y,求 .
.
您最近一年使用:0次
解题方法
7 . 已知函数 ,记
,记 ,且
,且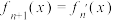 ,
,
(1)求 ,
,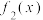 ;
;
(2)设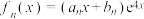 ,
, ,
,
(ⅰ)证明:数列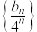 是等差数列;
是等差数列;
(ⅱ)数列 的前n项和为
的前n项和为 ,且对任意的
,且对任意的 ,满足
,满足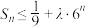 ,求
,求 的取值范围.
的取值范围.
 ,记
,记 ,且
,且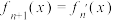 ,
,
(1)求
 ,
,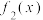 ;
;(2)设
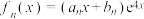 ,
, ,
,(ⅰ)证明:数列
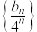 是等差数列;
是等差数列;(ⅱ)数列
 的前n项和为
的前n项和为 ,且对任意的
,且对任意的 ,满足
,满足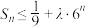 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
8 . 对于数列 ,如果存在正整数
,如果存在正整数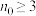 ,当任意正整数
,当任意正整数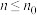 时均有
时均有 ,则称
,则称 为
为 的“
的“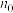 项递增相伴数列”.若
项递增相伴数列”.若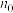 可取任意的正整数,则称
可取任意的正整数,则称 为
为 的“无限递增相伴数列”.
的“无限递增相伴数列”.
(1)已知 ,请写出一个数列
,请写出一个数列 的“无限递增相伴数列
的“无限递增相伴数列 ”,并说明理由?
”,并说明理由?
(2)若 满足
满足 ,其中
,其中 是首项
是首项 的等差数列,当
的等差数列,当 为
为 的“无限递增相伴数列”时,求
的“无限递增相伴数列”时,求 的通项公式:
的通项公式:
(3)已知等差数列 和正整数等比数列
和正整数等比数列 满足:
满足: ,其中k是正整数,求证:存在正整数k,使得
,其中k是正整数,求证:存在正整数k,使得 为
为 的“2024项递增相伴数列”.
的“2024项递增相伴数列”.
 ,如果存在正整数
,如果存在正整数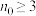 ,当任意正整数
,当任意正整数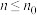 时均有
时均有 ,则称
,则称 为
为 的“
的“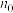 项递增相伴数列”.若
项递增相伴数列”.若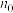 可取任意的正整数,则称
可取任意的正整数,则称 为
为 的“无限递增相伴数列”.
的“无限递增相伴数列”.(1)已知
 ,请写出一个数列
,请写出一个数列 的“无限递增相伴数列
的“无限递增相伴数列 ”,并说明理由?
”,并说明理由?(2)若
 满足
满足 ,其中
,其中 是首项
是首项 的等差数列,当
的等差数列,当 为
为 的“无限递增相伴数列”时,求
的“无限递增相伴数列”时,求 的通项公式:
的通项公式:(3)已知等差数列
 和正整数等比数列
和正整数等比数列 满足:
满足: ,其中k是正整数,求证:存在正整数k,使得
,其中k是正整数,求证:存在正整数k,使得 为
为 的“2024项递增相伴数列”.
的“2024项递增相伴数列”.
您最近一年使用:0次
2024-06-14更新
|
370次组卷
|
3卷引用:四川省成都市成华区嘉祥外国语学校2025届高三上学期期中考试数学试题
9 . 已知数列 满足
满足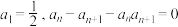 .
.
(1)求 的通项公式;
的通项公式;
(2)若数列 满足,
满足,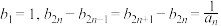 ,求证:
,求证: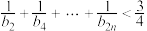 .
.
 满足
满足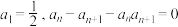 .
.(1)求
 的通项公式;
的通项公式;(2)若数列
 满足,
满足,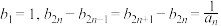 ,求证:
,求证: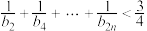 .
.
您最近一年使用:0次
10 . 在 (
( )个不同数的排列
)个不同数的排列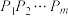 中,若
中,若 时有
时有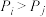 (即前面某数大于后面某数),则称
(即前面某数大于后面某数),则称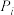 与
与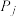 构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.例如,三个数的排列
构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.例如,三个数的排列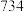 中,因为
中,因为 ,
, ,称 7与3,7与4均构成逆序,而
,称 7与3,7与4均构成逆序,而 ,3与4不构成逆序,于是排列
,3与4不构成逆序,于是排列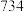 的逆序数为2.记排列
的逆序数为2.记排列 的逆序数为
的逆序数为 .
.
(1)求 ,
, ,
, ,并写出
,并写出 的表达式;
的表达式;
(2)设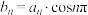 ,求数列
,求数列 的前
的前 项和;
项和;
(3)设数列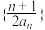 的前
的前 项和为
项和为 ,证明
,证明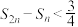 .
.
 (
( )个不同数的排列
)个不同数的排列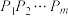 中,若
中,若 时有
时有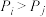 (即前面某数大于后面某数),则称
(即前面某数大于后面某数),则称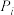 与
与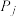 构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.例如,三个数的排列
构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.例如,三个数的排列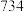 中,因为
中,因为 ,
, ,称 7与3,7与4均构成逆序,而
,称 7与3,7与4均构成逆序,而 ,3与4不构成逆序,于是排列
,3与4不构成逆序,于是排列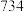 的逆序数为2.记排列
的逆序数为2.记排列 的逆序数为
的逆序数为 .
.(1)求
 ,
, ,
, ,并写出
,并写出 的表达式;
的表达式;(2)设
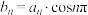 ,求数列
,求数列 的前
的前 项和;
项和;(3)设数列
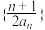 的前
的前 项和为
项和为 ,证明
,证明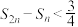 .
.
您最近一年使用:0次



