解题方法
1 . 在一定的环境下,某种食品的保质期为正整数 ,根据统计数据,它近似满足以下规律:对任意正整数
,根据统计数据,它近似满足以下规律:对任意正整数 ,保质期恰好为
,保质期恰好为 的该食品在所有保质期不小于
的该食品在所有保质期不小于 的该食品中的占比为
的该食品中的占比为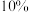 .记该食品的保质期为
.记该食品的保质期为 为事件
为事件 ,该食品的保质期不小于
,该食品的保质期不小于 为事件
为事件 :则
:则
______ ,
______ .
 ,根据统计数据,它近似满足以下规律:对任意正整数
,根据统计数据,它近似满足以下规律:对任意正整数 ,保质期恰好为
,保质期恰好为 的该食品在所有保质期不小于
的该食品在所有保质期不小于 的该食品中的占比为
的该食品中的占比为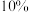 .记该食品的保质期为
.记该食品的保质期为 为事件
为事件 ,该食品的保质期不小于
,该食品的保质期不小于 为事件
为事件 :则
:则

您最近一年使用:0次
名校
2 . 已知各项均不为零的数列 的前
的前 项和为
项和为 ,
, ,
,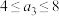 ,
,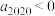 ,且
,且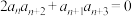 ,则
,则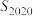 的最大值等于
的最大值等于_________ .
 的前
的前 项和为
项和为 ,
, ,
,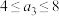 ,
,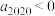 ,且
,且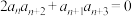 ,则
,则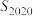 的最大值等于
的最大值等于
您最近一年使用:0次
2023-02-06更新
|
831次组卷
|
4卷引用:上海市行知中学2020-2021学年高二下学期期中数学试题
上海市行知中学2020-2021学年高二下学期期中数学试题(已下线)高二下期中真题精选(压轴40题专练)(已下线)期中真题必刷压轴50题专练-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)福建省宁德第一中学2020-2021学年高二上学期开学检测数学试题
名校
3 . 如图,在 中,
中, 是
是 边上一点,且
边上一点,且 ,
, 为直线
为直线 上一点列,满足:
上一点列,满足: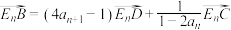 ,且
,且 ,则
,则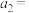
___________ ,设数列 ,则
,则 的通项公式为
的通项公式为___________ .
 中,
中, 是
是 边上一点,且
边上一点,且 ,
, 为直线
为直线 上一点列,满足:
上一点列,满足: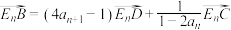 ,且
,且 ,则
,则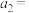
 ,则
,则 的通项公式为
的通项公式为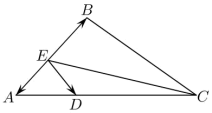
您最近一年使用:0次
2022-12-05更新
|
1362次组卷
|
7卷引用:福建省厦门外国语学校2024届高三上学期期中考试数学试题
福建省厦门外国语学校2024届高三上学期期中考试数学试题黑龙江省哈尔滨市第九中学校2022-2023学年高三上学期第三次月考数学试题天津市滨海新区大港第一中学2022-2023学年高三上学期1月阶段性测试数学试题江苏省盐城市响水中学2022-2023学年高二下学期期末模拟数学试题(已下线)专题05 数列 第一讲 数列的递推关系(分层练)(已下线)【讲】专题10 数列与其它知识的交汇问题(已下线)【练】 专题9 与图表有关的数列问题
4 . 2022年北京冬奥会开幕式中,当《雪花》这个节目开始后,一片巨大的“雪花”呈现在舞台中央,十分壮观.理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1904年研究的一种分形曲线.如图是“雪花曲线”的一种形成过程:从一个正三角形开始,把每条边分成三等份,然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程

若第1个图中的三角形的周长为1,则第n个图形的周长为___________ ;若第1个图中的三角形的面积为1,则第n个图形的面积为___________ .

若第1个图中的三角形的周长为1,则第n个图形的周长为
您最近一年使用:0次
2022-03-16更新
|
3858次组卷
|
16卷引用:浙江省杭州学军中学西溪校区2021-2022学年高二下学期4月期中数学试题
浙江省杭州学军中学西溪校区2021-2022学年高二下学期4月期中数学试题(已下线)高中数学 高二下-4湖北省八市2022届高三下学期3月联考数学试题江苏省镇江市扬中市第二高级中学2021-2022学年高二下学期3月阶段测试数学试题(已下线)专题20 科赫曲线(已下线)考点15 数列综合问题-1-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)天津市耀华中学2022-2023学年高三上学期统练(二)数学试题福建省福州第八中学2023届高三上学期质检四数学试题浙江省金华十校2022-2023学年高二上学期期末模拟数学试题辽宁省大连市庄河市高级中学2022-2023学年高二上学期12月月考数学试题山西省朔州市怀仁市2023届高三二模数学试题(已下线)专题05 数列(已下线)押新高考第16题 数列性质及其应用(已下线)专题10 数列通项公式的求法 微点2 累加法重庆市第八中学校2023-2024学年高二下学期入学适应性训练数学试题(已下线)数列的综合应用
名校
解题方法
5 . 把数列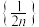 的所有项按照从大到小,左大右小的原则写成如图所示的数表,第
的所有项按照从大到小,左大右小的原则写成如图所示的数表,第 行有
行有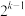 个数,第
个数,第 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则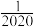 可记为
可记为_________ .
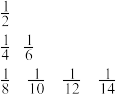
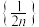 的所有项按照从大到小,左大右小的原则写成如图所示的数表,第
的所有项按照从大到小,左大右小的原则写成如图所示的数表,第 行有
行有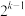 个数,第
个数,第 行的第
行的第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则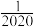 可记为
可记为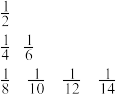
您最近一年使用:0次
2020-04-30更新
|
556次组卷
|
2卷引用:浙江省宁波市北仑中学2019-2020学年高一(2-10班)下学期期中数学试题
6 . 将一个数列中部分项按原来的先后次序排列所成的一个新数列称为原数列的一个子数列,如果数列存在成等比数列的子数列,那么称该数列为“弱等比数列”.已知 ,设区间
,设区间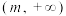 内的三个正整数
内的三个正整数 ,
, ,
, 满足:数列
满足:数列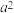 ,
, ,
,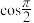 ,
, 为“弱等比数列”,则
为“弱等比数列”,则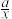 的最小值为
的最小值为________ .
 ,设区间
,设区间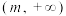 内的三个正整数
内的三个正整数 ,
, ,
, 满足:数列
满足:数列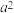 ,
, ,
,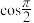 ,
, 为“弱等比数列”,则
为“弱等比数列”,则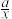 的最小值为
的最小值为
您最近一年使用:0次
2020-02-14更新
|
1015次组卷
|
2卷引用:江苏省南通市海安高级中学2021-2022学年高三上学期期中模拟数学试题
名校
解题方法
7 . 已知非空集合M满足M⊆{0,1,2,…n}(n≥2,n∈N+).若存在非负整数k(k≤n),使得当a∈M时,均有2k-a∈M,则称集合M具有性质P.设具有性质P的集合M的个数为f(n),求 的值为
的值为______ .
 的值为
的值为
您最近一年使用:0次
2019-05-04更新
|
1338次组卷
|
3卷引用:【全国百强校】江苏省无锡市第一中学2018-2019学年高二第二学期期中数学(理科)试题
【全国百强校】江苏省无锡市第一中学2018-2019学年高二第二学期期中数学(理科)试题(已下线)专题03 集合的运算压轴题型-2021-2022学年高一《新题速递·数学》(人教A版2019)上海市浦东复旦附中分校2023-2024学年高三下学期3月月考数学试题
名校
8 . 已知数列 的前
的前 项和为
项和为 ,且数列
,且数列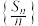 是首项为3,公差为2的等差数列,若
是首项为3,公差为2的等差数列,若 ,数列
,数列 的前
的前 项和为
项和为 ,则使得
,则使得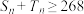 成立的
成立的 的最小值为
的最小值为__________ .
 的前
的前 项和为
项和为 ,且数列
,且数列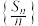 是首项为3,公差为2的等差数列,若
是首项为3,公差为2的等差数列,若 ,数列
,数列 的前
的前 项和为
项和为 ,则使得
,则使得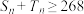 成立的
成立的 的最小值为
的最小值为
您最近一年使用:0次
2018-08-29更新
|
2570次组卷
|
5卷引用:上海市上海中学2018-2019学年高三上学期期中数学试题
9 . 已知集合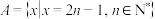 ,
,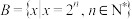 .将
.将 的所有元素从小到大依次排列构成一个数列
的所有元素从小到大依次排列构成一个数列 .记
.记 为数列
为数列 的前n项和,则使得
的前n项和,则使得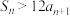 成立的n的最小值为
成立的n的最小值为________ .
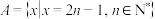 ,
,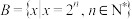 .将
.将 的所有元素从小到大依次排列构成一个数列
的所有元素从小到大依次排列构成一个数列 .记
.记 为数列
为数列 的前n项和,则使得
的前n项和,则使得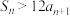 成立的n的最小值为
成立的n的最小值为
您最近一年使用:0次
2018-06-10更新
|
10274次组卷
|
49卷引用:上海市西南位育中学2019-2020学年高三上学期期中数学试题
上海市西南位育中学2019-2020学年高三上学期期中数学试题2018年全国普通高等学校招生统一考试数学(江苏卷)(已下线)2018年高考题及模拟题汇编 【理科】4.数列与不等式(已下线)2018年高考题及模拟题汇编 【文科】4.数列与不等式江西省都昌县第一中学2019届高三上学期第一次调研考试理科数学【全国百强校】浙江省杭州第十四中学2019届高三12月月考试数学试题(已下线)10.算法、推理与证明、复数[文] -《备战2020年高考精选考点专项突破题集》(已下线)专题14 数列的综合应用-《巅峰冲刺2020年高考之二轮专项提升》(江苏)专题10 算法、推理与证明、复数[理]-《备战2020年高考精选考点专项突破题集》(已下线)专题12 数列——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题12 数列——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题08 数列-五年(2016-2020)高考数学(文)真题分项(已下线)专题08 数列-五年(2016-2020)高考数学(理)真题分项(已下线)考点20 数列的综合运用-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)考点19 数列通项与求和与通项-2021年高考数学三年真题与两年模拟考点分类解读(新高考地区专用)(已下线)专题19 数列的求和问题-十年(2011-2020)高考真题数学分项(已下线)考点23 数列的综合应用-备战2021年高考数学(文)一轮复习考点一遍过(已下线)专题33 算法、复数、推理与证明-十年(2011-2020)高考真题数学分项(六)江苏省常州市第三中学2020-2021学年高二上学期10月学情检测数学试题(已下线)第23练 等比数列-2021年高考数学(理)一轮复习小题必刷(已下线)第22练 等差数列-2021年高考数学(理)一轮复习小题必刷(已下线)专题18+新定义题、推理与证明-2021高考数学(理)高频考点、热点题型归类强化(已下线)第四章 数列测试 B提高练湖南省益阳市桃江县第一中学2020-2021学年高二下学期入学考试数学试题(已下线)专题08 数列的通项、求和及综合应用 第一篇 热点、难点突破篇(练)-2021年高考数学二轮复习讲练测(浙江专用))(已下线)专题20 数列综合问题的探究-2021年高考数学二轮优化提升专题训练(新高考地区专用)【学科网名师堂】(已下线)预测07 数列-【临门一脚】2020年高考数学三轮冲刺过关(江苏专用)(已下线)2021年高三数学二轮复习讲练测之练案 专题十九 数列中的最值问题(文理通用)(已下线)数学-2021年高考考前20天终极冲刺攻略(三)(新高考地区专用)【学科网名师堂】 (6月1日)(已下线)【新教材精创】第五章-复习与小结 -B提高练 上海市大同中学2021届高三上学期开学考试数学试题(已下线)模块07 数列与数学归纳法-2022年高考数学一轮复习小题多维练(上海专用)(已下线)专题08 数列-五年(2017-2021)高考数学真题分项汇编(文科+理科)苏教版(2019) 选修第一册 一蹴而就 第4章 单元整合(已下线)专题15 盘点与数列有关的最值问题——备战2022年高考数学二轮复习常考点专题突破(已下线)专题22 等差等比数列性质的巧用-学会解题之高三数学万能解题模板【2022版】(已下线)专题24 数列求和的常见方法-学会解题之高三数学万能解题模板【2022版】上海市松江二中2023届高三上学期9月月考数学试题上海市曹杨第二中学2023届高三上学期12月月考数学试题沪教版(2020) 一轮复习 堂堂清 第四单元 综合练习(已下线)专题6.3 等比数列及其前n项和(练)-江苏版《2020年高考一轮复习讲练测》上海市吴淞中学2021-2022学年高二上学期期末数学试题(已下线)专题11 押全国卷(理科)第4、8题 数列江苏省扬州中学2022-2023学年高二下学期3月月考数学试题北京市海淀区北京理工大附中高三上学期12月练习数学试题(已下线)专题05 数列 第三讲 数列与不等关系(分层练)(已下线)专题06 数列小题(理科)-2(已下线)专题05 数列小题(7类题型,文科)上海市大同中学2023-2024学年高一下学期5月月考数学试题
名校
解题方法
10 . 在 中,
中, ,
, 分别是边
分别是边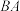 ,
, 的中点,
的中点, ,
, 分别是线段
分别是线段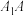 ,
, 的中点,…,
的中点,…, ,
, 分别是线段
分别是线段 ,
,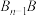 (
( ,
, )的中点,设数列
)的中点,设数列 ,
, 满足:向量
满足:向量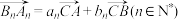 ,有下列四个命题:
,有下列四个命题:
①数列 是单调递增数列,数列
是单调递增数列,数列 是单调递减数列;
是单调递减数列;
②数列 是等比数列;
是等比数列;
③数列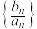 有最小值,无最大值;
有最小值,无最大值;
④若 中,
中, ,
, ,则
,则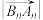 最小时,
最小时,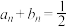
其中真命题是__________ .
 中,
中, ,
, 分别是边
分别是边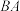 ,
, 的中点,
的中点, ,
, 分别是线段
分别是线段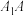 ,
, 的中点,…,
的中点,…, ,
, 分别是线段
分别是线段 ,
,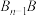 (
( ,
, )的中点,设数列
)的中点,设数列 ,
, 满足:向量
满足:向量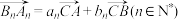 ,有下列四个命题:
,有下列四个命题:①数列
 是单调递增数列,数列
是单调递增数列,数列 是单调递减数列;
是单调递减数列;②数列
 是等比数列;
是等比数列;③数列
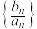 有最小值,无最大值;
有最小值,无最大值;④若
 中,
中, ,
, ,则
,则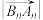 最小时,
最小时,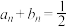
其中真命题是
您最近一年使用:0次
2018-03-09更新
|
1547次组卷
|
3卷引用:北京市第一六六中学2022-2023学年高二下学期期中诊断数学试题



