解题方法
1 . 如图,在以 为顶点的五面体中,四边形
为顶点的五面体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形,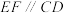 ,且平面
,且平面 平面
平面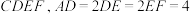 .
.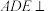 平面
平面 ;
;
(2)求平面 和平面
和平面 夹角的余弦值.
夹角的余弦值.
 为顶点的五面体中,四边形
为顶点的五面体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形,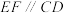 ,且平面
,且平面 平面
平面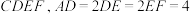 .
.
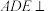 平面
平面 ;
;(2)求平面
 和平面
和平面 夹角的余弦值.
夹角的余弦值.
您最近半年使用:0次
解题方法
2 . 在三棱锥 中,
中,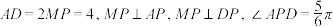 ,则三棱锥
,则三棱锥 的外接球的体积为( )
的外接球的体积为( )
 中,
中,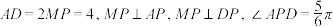 ,则三棱锥
,则三棱锥 的外接球的体积为( )
的外接球的体积为( )A.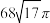 | B.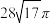 |
C.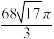 | D. |
您最近半年使用:0次
名校
3 . 如图,在直三棱柱 中,
中,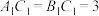 ,
,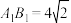 ,
, 为
为 的中点.
的中点.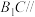 平面
平面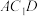 .
.
(2)若以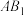 为直径的球的表面积为
为直径的球的表面积为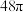 ,求二面角
,求二面角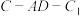 的余弦值.
的余弦值.
 中,
中,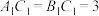 ,
,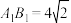 ,
, 为
为 的中点.
的中点.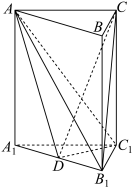
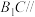 平面
平面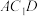 .
.(2)若以
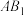 为直径的球的表面积为
为直径的球的表面积为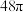 ,求二面角
,求二面角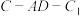 的余弦值.
的余弦值.
您最近半年使用:0次
2024-04-20更新
|
1141次组卷
|
3卷引用:四川省雅安市2024届高三下学期4月联考数学(理)试题
解题方法
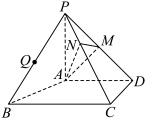
4 . 已知在四棱锥 中,
中, 平面
平面 ,四边形
,四边形 是直角梯形,满足
是直角梯形,满足 ,若
,若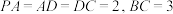 ,点
,点 为
为 的中点,点
的中点,点 为
为 的三等分点(靠近点
的三等分点(靠近点 ).
). 平面
平面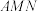 ;
;
(2)若线段 上的点
上的点 在平面
在平面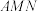 内,求
内,求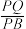 的值.
的值.
 中,
中, 平面
平面 ,四边形
,四边形 是直角梯形,满足
是直角梯形,满足 ,若
,若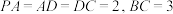 ,点
,点 为
为 的中点,点
的中点,点 为
为 的三等分点(靠近点
的三等分点(靠近点 ).
).
 平面
平面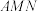 ;
;(2)若线段
 上的点
上的点 在平面
在平面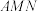 内,求
内,求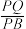 的值.
的值.
您最近半年使用:0次
名校
解题方法
5 . 如图,菱形 的对角线
的对角线 与
与 交于点
交于点 ,
, 是
是 的中位线,
的中位线, 与
与 交于点
交于点 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形﹐且
旋转过程中的一个图形﹐且 平面
平面 .给出下列结论:
.给出下列结论: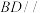 平面
平面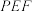 ;
;
②平面 平面
平面 ;
;
③“直线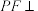 直线
直线 ”始终不成立.
”始终不成立.
其中所有正确结论的序号为( )
 的对角线
的对角线 与
与 交于点
交于点 ,
, 是
是 的中位线,
的中位线, 与
与 交于点
交于点 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形﹐且
旋转过程中的一个图形﹐且 平面
平面 .给出下列结论:
.给出下列结论: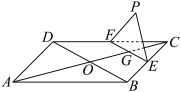
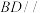 平面
平面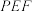 ;
;②平面
 平面
平面 ;
;③“直线
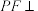 直线
直线 ”始终不成立.
”始终不成立.其中所有正确结论的序号为( )
| A.①②③ | B.①② | C.①③ | D.②③ |
您最近半年使用:0次
2024-04-20更新
|
594次组卷
|
6卷引用:四川省广安市2024届高三第二次诊断性考试数学(文)试题
四川省广安市2024届高三第二次诊断性考试数学(文)试题2024届四川省遂宁市等3地高三二模文科数学试题四川省雅安市2024届高三下学期二诊数学(文)试题四川省乐山市2024届高三第二次调查研究考试文科数学试题河南省南阳市西峡县第一高级中学2023-2024学年高二下学期第一次月考数学试卷(已下线)专题20 空间直线、平面的垂直-《重难点题型·高分突破》(人教A版2019必修第二册)
6 . 设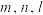 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,则下列说法中正确的是( )
是两个不同的平面,则下列说法中正确的是( )
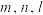 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,则下列说法中正确的是( )
是两个不同的平面,则下列说法中正确的是( )A.若 ,则 ,则 | B.若 ,则 ,则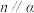 |
C.若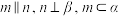 ,则 ,则 | D.若 ,则 ,则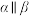 |
您最近半年使用:0次
2024-04-20更新
|
965次组卷
|
3卷引用:四川省南充市2024届高三高考适应性考试(二诊)理科数学试题
四川省南充市2024届高三高考适应性考试(二诊)理科数学试题四川省南充市2024届高三高考适应性考试(二诊)文科数学试题(已下线)专题20 空间直线、平面的垂直-《重难点题型·高分突破》(人教A版2019必修第二册)
解题方法
7 . 如图1,在矩形 中,
中,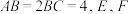 分别为线段
分别为线段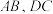 的中点,沿
的中点,沿 把
把 折起,使得
折起,使得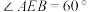 ,如图2所示,
,如图2所示,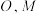 分别为线段
分别为线段 的中点,
的中点,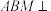 平而
平而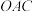 ;
;
(2)求二面角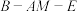 的余弦值.
的余弦值.
 中,
中,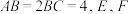 分别为线段
分别为线段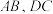 的中点,沿
的中点,沿 把
把 折起,使得
折起,使得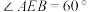 ,如图2所示,
,如图2所示,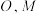 分别为线段
分别为线段 的中点,
的中点,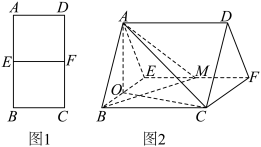
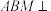 平而
平而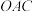 ;
;(2)求二面角
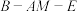 的余弦值.
的余弦值.
您最近半年使用:0次
8 . 已知 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列说法正确的是( )
是两个不同的平面,则下列说法正确的是( )
 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列说法正确的是( )
是两个不同的平面,则下列说法正确的是( )A.若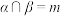 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则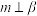 |
C.若 , ,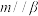 , , ,则 ,则 |
D.若 , , , ,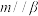 , , ,则 ,则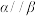 |
您最近半年使用:0次
9 . 已知 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,给出下列结论,其中正确结论的个数是( )
是两个不同的平面,给出下列结论,其中正确结论的个数是( )
①若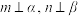 ,且
,且 ,则
,则
②若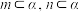 且
且 ,则
,则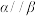
③若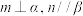 ,且
,且 ,则
,则
④若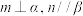 ,且
,且 ,则
,则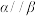
 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,给出下列结论,其中正确结论的个数是( )
是两个不同的平面,给出下列结论,其中正确结论的个数是( )①若
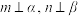 ,且
,且 ,则
,则
②若
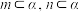 且
且 ,则
,则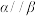
③若
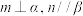 ,且
,且 ,则
,则
④若
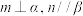 ,且
,且 ,则
,则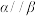
| A.1 | B.2 | C.3 | D.4 |
您最近半年使用:0次
名校
解题方法
10 . 已知球内接正四棱锥 的高为
的高为 ,
, 、
、 相交于
相交于 ,球的表面积为
,球的表面积为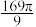 ,若
,若 为
为 中点.
中点.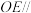 平面
平面 ;
;
(2)求三棱锥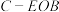 的体积.
的体积.
 的高为
的高为 ,
, 、
、 相交于
相交于 ,球的表面积为
,球的表面积为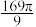 ,若
,若 为
为 中点.
中点.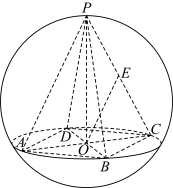
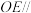 平面
平面 ;
;(2)求三棱锥
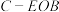 的体积.
的体积.
您最近半年使用:0次



