1 . 如图,三棱柱 中,
中, 平面
平面 ,
, ,
,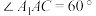 .过侧棱
.过侧棱 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.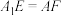 ;
;
(2)若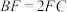 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, 平面
平面 ,
, ,
,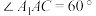 .过侧棱
.过侧棱 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.
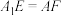 ;
;(2)若
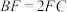 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
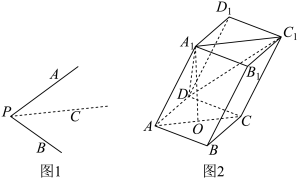
2 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记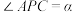 ,
,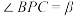 ,
, ,二面角
,二面角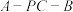 的大小为
的大小为 ,则
,则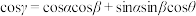 .如图2,四棱柱
.如图2,四棱柱 中,
中,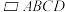 为菱形,
为菱形, ,
,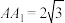 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.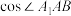 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: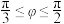 ;
;
(3)过点 作平面
作平面 ,使平面
,使平面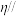 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记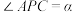 ,
,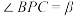 ,
, ,二面角
,二面角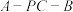 的大小为
的大小为 ,则
,则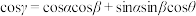 .如图2,四棱柱
.如图2,四棱柱 中,
中,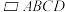 为菱形,
为菱形, ,
,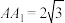 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
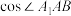 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: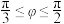 ;
;(3)过点
 作平面
作平面 ,使平面
,使平面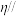 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
您最近一年使用:0次
2024-07-20更新
|
782次组卷
|
6卷引用:河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题
河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2(已下线)拔高点突破04 新情景、新定义下的立体几何问题(六大题型)-1湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题山东省德州市夏津育中万隆中英文高级中学2024-2025学年高二上学期第一次月考数学试题
名校
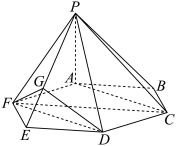
3 . 如图,在六棱锥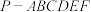 中,平面
中,平面 是边长为
是边长为 的正六边形,
的正六边形, 平面
平面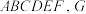 为棱
为棱 上一点,且
上一点,且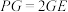 .
.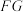
 平面
平面 ;
;
(2)若 ,求平面
,求平面 与平面
与平面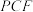 夹角的余弦值.
夹角的余弦值.
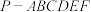 中,平面
中,平面 是边长为
是边长为 的正六边形,
的正六边形, 平面
平面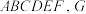 为棱
为棱 上一点,且
上一点,且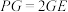 .
.
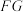
 平面
平面 ;
;(2)若
 ,求平面
,求平面 与平面
与平面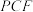 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
名校
4 . 如图,已知在圆柱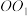 中,A,B,C是底面圆O上的三个点,且线段
中,A,B,C是底面圆O上的三个点,且线段 为圆O的直径,
为圆O的直径, ,
, 为圆柱上底面上的两点,且矩形
为圆柱上底面上的两点,且矩形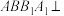 平面
平面 ,D,E分别是
,D,E分别是 ,
,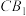 的中点.
的中点. 平面
平面 .
.
(2)若 是等腰直角三角形,且
是等腰直角三角形,且 平面
平面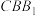 ,求平面
,求平面 与平面
与平面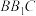 的夹角的正弦值.
的夹角的正弦值.
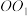 中,A,B,C是底面圆O上的三个点,且线段
中,A,B,C是底面圆O上的三个点,且线段 为圆O的直径,
为圆O的直径, ,
, 为圆柱上底面上的两点,且矩形
为圆柱上底面上的两点,且矩形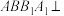 平面
平面 ,D,E分别是
,D,E分别是 ,
,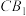 的中点.
的中点.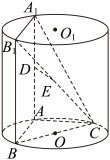
 平面
平面 .
.(2)若
 是等腰直角三角形,且
是等腰直角三角形,且 平面
平面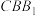 ,求平面
,求平面 与平面
与平面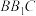 的夹角的正弦值.
的夹角的正弦值.
您最近一年使用:0次
2024-03-23更新
|
1469次组卷
|
3卷引用:河北省沧州市沧县中学2024届高三下学期3月高考模拟测试数学试题
解题方法
5 . 如图,正方体 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且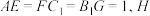 是棱
是棱 上一点.
上一点.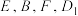 四点共面;
四点共面;
(2)若平面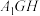 ∥平面
∥平面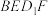 ,求证:
,求证: 为
为 的中点.
的中点.
 的棱长为3,点
的棱长为3,点 在棱
在棱 上,点
上,点 在棱
在棱 上,
上, 在棱
在棱 上,且
上,且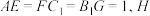 是棱
是棱 上一点.
上一点.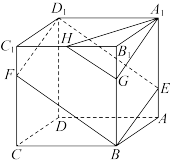
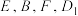 四点共面;
四点共面;(2)若平面
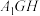 ∥平面
∥平面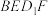 ,求证:
,求证: 为
为 的中点.
的中点.
您最近一年使用:0次
2023-08-06更新
|
808次组卷
|
7卷引用:河北省承德市重点高中2022-2023学年高一下学期5月月考数学试题
河北省承德市重点高中2022-2023学年高一下学期5月月考数学试题河北省沧州市东光县等三县联考2022-2023学年高一下学期4月月考数学试题(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】(已下线)8.5.2平面与平面平行(已下线)6.4.2平面与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)专题13.5空间平面与平面的位置关系-重难点突破及混淆易错规避(苏教版2019必修第二册)(已下线)专题3.5空间直线、平面的平行-重难点突破及混淆易错规避(人教A版2019必修第二册)
名校
解题方法
6 . 如图,在三棱柱 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.

 ;
;
(2)在线段CD上是否存在一点 ,使得平面
,使得平面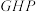
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.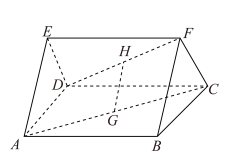


 ;
;(2)在线段CD上是否存在一点
 ,使得平面
,使得平面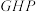
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
您最近一年使用:0次
2023-04-13更新
|
3311次组卷
|
11卷引用:河北定州中学2022-2023学年高一下学期5月月考数学试题
河北定州中学2022-2023学年高一下学期5月月考数学试题浙江省宁波市三锋教研联盟2022-2023学年高一下学期期中联考数学试题(已下线)立体几何专题:立体几何探索性问题的8种考法(已下线)13.2.4 平面与平面的位置关系 (1)江西省宜春市第十中学2024届高二上学期开学检测数学试题新疆阿克苏市实验中学2022-2023学年高一下学期第三次月考数学试题(已下线)8.5.3 平面与平面平行【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)(已下线)专题突破:空间几何体的动点探究问题-同步题型分类归纳讲与练(人教A版2019必修第二册)【课后练】第4.4节综合训练 课后作业-湘教版(2019)必修(第二册) 第4章 立体几何初步(已下线)第四节直线、平面平行的判定与性质【同步课时】基础卷
名校
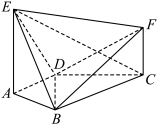
7 . 如图, 平面
平面 ,
,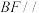 平面
平面 ,
,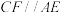 ,
, ,
,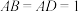 ,
, .
.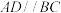 ;
;
(2)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 平面
平面 ,
,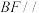 平面
平面 ,
,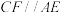 ,
, ,
,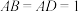 ,
, .
.
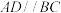 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2023-01-01更新
|
664次组卷
|
2卷引用:河北省保定市高碑店市崇德实验中学2024届高三下学期3月月考数学试题
名校
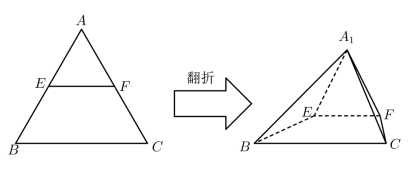
8 . 已知 是边长为4的等边三角形,E,F分别是
是边长为4的等边三角形,E,F分别是 ,
, 的中点,将
的中点,将 沿着
沿着 翻折,得到四棱锥
翻折,得到四棱锥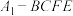 ,平面
,平面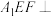 平面
平面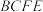 ,平面
,平面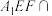 平面
平面 .
.
(1)求证: 平面
平面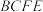 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求点C到平面 的距离.
的距离.
 是边长为4的等边三角形,E,F分别是
是边长为4的等边三角形,E,F分别是 ,
, 的中点,将
的中点,将 沿着
沿着 翻折,得到四棱锥
翻折,得到四棱锥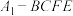 ,平面
,平面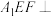 平面
平面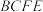 ,平面
,平面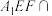 平面
平面 .
.
(1)求证:
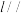 平面
平面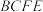 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求点C到平面
 的距离.
的距离.
您最近一年使用:0次
2022-10-12更新
|
538次组卷
|
2卷引用:河北省故城县高级中学2022-2023学年高二上学期第一次月考数学试题
名校
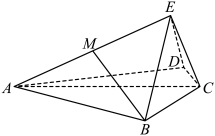
9 . 如图,四棱锥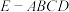 ,
,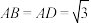 ,
,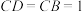 ,
,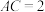 ,平面
,平面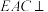 平面
平面 ,平面
,平面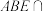 平面
平面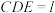 .
. 为线段
为线段 中点,求证:
中点,求证: ;
;
(2)若 ,
, ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
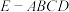 ,
,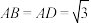 ,
,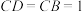 ,
,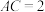 ,平面
,平面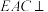 平面
平面 ,平面
,平面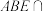 平面
平面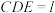 .
.
 为线段
为线段 中点,求证:
中点,求证: ;
;(2)若
 ,
, ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-05-16更新
|
688次组卷
|
2卷引用:河北省邯郸市2022届高三5月模拟数学试题
名校
10 . 如图,三棱台 的底面是正三角形,平面
的底面是正三角形,平面 平面
平面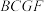 ,
,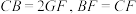 .
.
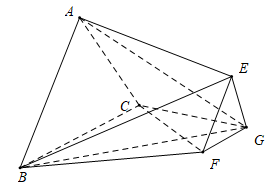
(1)求证: ;
;
(2)若 ,求直线
,求直线 与平面
与平面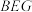 所成角的正弦值.
所成角的正弦值.
 的底面是正三角形,平面
的底面是正三角形,平面 平面
平面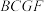 ,
,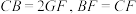 .
.
(1)求证:
 ;
;(2)若
 ,求直线
,求直线 与平面
与平面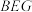 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2020-09-02更新
|
475次组卷
|
9卷引用:河北省冀州中学2018-2019学年高二下学期第二次月考数学(理)试题
河北省冀州中学2018-2019学年高二下学期第二次月考数学(理)试题【市级联考】安徽省合肥市2019届高三第二次教学质量检测数学(理)试题【全国百强校】重庆市南开中学2019届高三4月测试数学(理)试题【市级联考】山东省聊城市2019届高三三模试卷理科数学试题2019届浙江省绍兴一中高三下学期5月高考适应性考试数学试题浙江省温州市平阳中学2020届高三下学期3月高考模拟数学试题(已下线)第32讲 平面的基本性质与推论-2021年新高考数学一轮专题复习(新高考专版)四川省眉山市2020-2021学年高二上学期期末考试数学(理)试题(已下线)专题19 立体几何综合-2020年高考数学母题题源全揭秘(浙江专版)



