名校
解题方法
1 . 如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, 、
、 分别为
分别为 、
、 的中点,平面
的中点,平面 平面
平面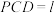 .
.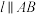 ;
;
(2)证明: ∥平面
∥平面 ;
;
(3)在线段 上是否存在一点
上是否存在一点 ,使
,使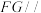 平面
平面 ?若存在,求出
?若存在,求出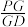 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,底面
中,底面 为平行四边形,
为平行四边形, 、
、 分别为
分别为 、
、 的中点,平面
的中点,平面 平面
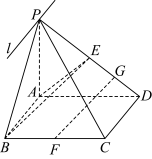
平面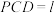 .
.
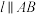 ;
;(2)证明:
 ∥平面
∥平面 ;
;(3)在线段
 上是否存在一点
上是否存在一点 ,使
,使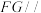 平面
平面 ?若存在,求出
?若存在,求出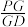 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-08-14更新
|
286次组卷
|
2卷引用:山西省太原市第五中学2023-2024学年高一下学期5月月考数学试题
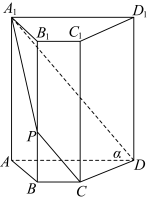
2 . 如图,四棱柱 中,
中, 平面
平面 ,平面
,平面 平面
平面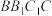 .过
.过 ,
, ,
, 三点的平面记为
三点的平面记为 ,
, 与
与 的交点为
的交点为 ,
, .
.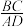 ;
;
(2)证明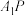 ,
, ,
, 三线共点,并求此四棱柱被平面
三线共点,并求此四棱柱被平面 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;
(3)若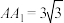 ,
,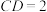 ,二面角
,二面角 的大小为
的大小为 ,求三棱台
,求三棱台 的体积.
的体积.
 中,
中, 平面
平面 ,平面
,平面 平面
平面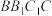 .过
.过 ,
, ,
, 三点的平面记为
三点的平面记为 ,
, 与
与 的交点为
的交点为 ,
, .
.
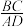 ;
;(2)证明
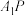 ,
, ,
, 三线共点,并求此四棱柱被平面
三线共点,并求此四棱柱被平面 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;(3)若
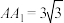 ,
,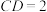 ,二面角
,二面角 的大小为
的大小为 ,求三棱台
,求三棱台 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
3 . 如图,在正三棱台 中,
中,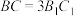 ,
,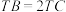 ,
, ,
, 分别是
分别是 ,
, 的中点,
的中点, 为
为 上一点.
上一点. 是
是 的中点,求证:
的中点,求证: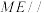 平面
平面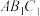 ;
;
(2)若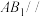 平面
平面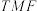 ,求点
,求点 的位置,并说明理由.
的位置,并说明理由.
 中,
中,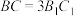 ,
,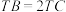 ,
, ,
, 分别是
分别是 ,
, 的中点,
的中点, 为
为 上一点.
上一点.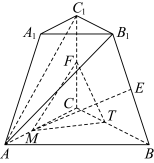
 是
是 的中点,求证:
的中点,求证: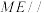 平面
平面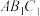 ;
;(2)若
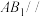 平面
平面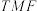 ,求点
,求点 的位置,并说明理由.
的位置,并说明理由.
您最近一年使用:0次
解题方法
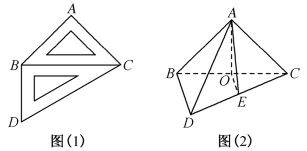
4 . 一副三角板如图(1),将其中的 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
(1)取 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面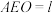 ,求证:
,求证: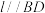 ;
;
(2)证明:平面 ⊥平面
⊥平面 ;
;
(3)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 沿
沿 折起,构造出如图(2)所示的三棱锥,
折起,构造出如图(2)所示的三棱锥, 为
为 的中点,连接
的中点,连接 ,使得
,使得 .
.
(1)取
 中点
中点 ,连接
,连接 ,设平面
,设平面 平面
平面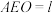 ,求证:
,求证: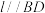 ;
;(2)证明:平面
 ⊥平面
⊥平面 ;
;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次



