1 . 如图所示的多面体中,四边形ABCD是菱形且 ,
, ,
, 平面ABCD,
平面ABCD,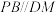 ,点N为PC上的动点.
,点N为PC上的动点.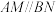 .
.
(2)求二面角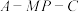 的正弦值.
的正弦值.
 ,
, ,
, 平面ABCD,
平面ABCD,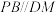 ,点N为PC上的动点.
,点N为PC上的动点.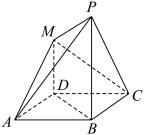
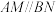 .
.(2)求二面角
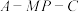 的正弦值.
的正弦值.
您最近一年使用:0次
2024-10-18更新
|
154次组卷
|
2卷引用:湖南省衡阳市衡阳县部分学校2024-2025学年高二上学期第一次月考数学测评卷(A卷)
名校
解题方法
2 . 在如图所示的直三棱柱 中,
中,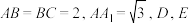 分别是线段
分别是线段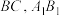 上的动点.
上的动点.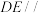 平面
平面 ,求证:
,求证: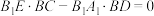 ;
;
(2)若 为正三角形,E是
为正三角形,E是 的中点,求二面角
的中点,求二面角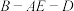 余弦值的最小值.
余弦值的最小值.
 中,
中,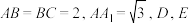 分别是线段
分别是线段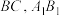 上的动点.
上的动点.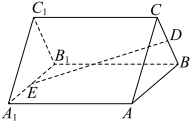
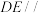 平面
平面 ,求证:
,求证: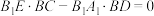 ;
;(2)若
 为正三角形,E是
为正三角形,E是 的中点,求二面角
的中点,求二面角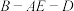 余弦值的最小值.
余弦值的最小值.
您最近一年使用:0次
名校
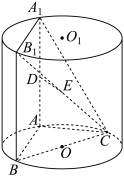
3 . 如图, ,
, 为圆柱
为圆柱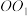 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
,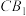 的中点,
的中点, 平面
平面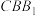 .
.
(1)证明:
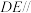 平面
平面 ;
;(2)若
 ,求平面
,求平面 与平面
与平面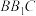 的夹角余弦值.
的夹角余弦值.
您最近一年使用:0次
名校
4 . 如图所示,圆台的上、下底面圆半径分别为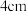 和
和 ,
,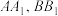 为圆台的两条不同的母线.
为圆台的两条不同的母线.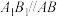 ;
;
(2)截面 与下底面所成的夹角大小为
与下底面所成的夹角大小为 ,且截面截得圆台上底面圆的劣弧
,且截面截得圆台上底面圆的劣弧 的长度为
的长度为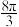 ,求截面
,求截面 的面积.
的面积.
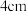 和
和 ,
,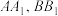 为圆台的两条不同的母线.
为圆台的两条不同的母线.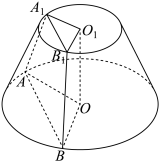
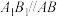 ;
;(2)截面
 与下底面所成的夹角大小为
与下底面所成的夹角大小为 ,且截面截得圆台上底面圆的劣弧
,且截面截得圆台上底面圆的劣弧 的长度为
的长度为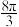 ,求截面
,求截面 的面积.
的面积.
您最近一年使用:0次
2024-01-26更新
|
1606次组卷
|
9卷引用:湖南省邵阳市2024届高三第一次联考数学试题
湖南省邵阳市2024届高三第一次联考数学试题湖南省长沙市长郡中学2024届高三下学期模拟(一)数学试卷(已下线)模块7 空间几何篇 第2讲:立体几何的截面问题【练】2024届高三新改革数学模拟预测训练一(九省联考题型)(已下线)2024年高考数学二轮复习测试卷(新题型,江苏专用)(已下线)第3套-复盘卷(已下线)微考点5-2 新高考新试卷结构立体几何解答题中与旋转体有关的问题(已下线)信息必刷卷01(江苏专用,2024新题型)(已下线)6.1 空间几何的体积与表面积
名校
5 . 如图所示,圆台的上、下底面圆半径分别为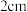 和
和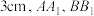 为圆台的两条不同的母线.
为圆台的两条不同的母线.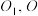 分别为圆台的上、下底面圆的圆心,且
分别为圆台的上、下底面圆的圆心,且 为等边三角形.
为等边三角形.
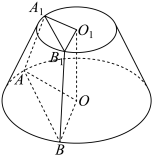
(1)求证:

 ;
;
(2)截面 与下底面所成的夹角大小为
与下底面所成的夹角大小为 ,求异面直线
,求异面直线 与
与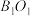 所成角的余弦值.
所成角的余弦值.
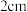 和
和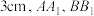 为圆台的两条不同的母线.
为圆台的两条不同的母线.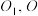 分别为圆台的上、下底面圆的圆心,且
分别为圆台的上、下底面圆的圆心,且 为等边三角形.
为等边三角形.
(1)求证:


 ;
;(2)截面
 与下底面所成的夹角大小为
与下底面所成的夹角大小为 ,求异面直线
,求异面直线 与
与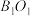 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024-01-24更新
|
1387次组卷
|
3卷引用:湖南省邵阳市2024届高三第一次联考数学试题
名校
6 . 如图, ,
, 为圆柱
为圆柱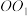 的母线,BC是底面圆O的直径,D,E分别是
的母线,BC是底面圆O的直径,D,E分别是 ,
,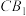 的中点,
的中点, 面
面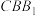 .
.

(1)证明: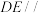 平面ABC;
平面ABC;
(2)若 ,求平面
,求平面 与平面BDC的夹角余弦值.
与平面BDC的夹角余弦值.
 ,
, 为圆柱
为圆柱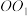 的母线,BC是底面圆O的直径,D,E分别是
的母线,BC是底面圆O的直径,D,E分别是 ,
,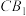 的中点,
的中点, 面
面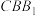 .
.
(1)证明:
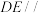 平面ABC;
平面ABC;(2)若
 ,求平面
,求平面 与平面BDC的夹角余弦值.
与平面BDC的夹角余弦值.
您最近一年使用:0次
2023-09-30更新
|
640次组卷
|
4卷引用:湖南省长沙市四校2022-2023学年高二上学期期中联考数学试题
名校
解题方法
7 . 如图,三棱柱 中,面
中,面 面
面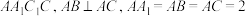 ,
,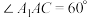 .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.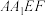 为平行四边形;
为平行四边形;
(2)若 到平面
到平面 的距离为
的距离为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,面
中,面 面
面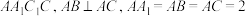 ,
,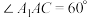 .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.
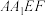 为平行四边形;
为平行四边形;(2)若
 到平面
到平面 的距离为
的距离为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-05-30更新
|
1549次组卷
|
7卷引用:湖南省怀化市2023届高三二模数学试题
21-22高一·湖南·课后作业
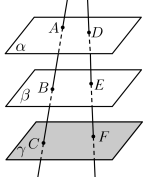
8 . 如图,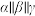 ,直线AC分别交平面
,直线AC分别交平面 ,
, ,
, 于点A,B,C,直线DF分别交平面
于点A,B,C,直线DF分别交平面 ,
, ,
, 于点D,E,F.求证:
于点D,E,F.求证: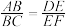 .
.
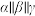 ,直线AC分别交平面
,直线AC分别交平面 ,
, ,
, 于点A,B,C,直线DF分别交平面
于点A,B,C,直线DF分别交平面 ,
, ,
, 于点D,E,F.求证:
于点D,E,F.求证: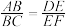 .
.
您最近一年使用:0次
2022-02-22更新
|
271次组卷
|
4卷引用:4.4.2 平面与平面垂直
(已下线)4.4.2 平面与平面垂直4.4.1 平面与平面平行的性质4.4.1 平面与平面平行(已下线)第10讲空间直线、平面的平行(核心考点讲与练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(原卷版)
9 . 如图,在五面体 中,四边形
中,四边形 是正方形,
是正方形,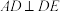 ,
,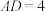 ,
,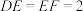 .
.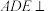 平面
平面 ;
;
(2)设 是
是 的中点,棱
的中点,棱 上是否存在点
上是否存在点 ,使得
,使得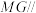 平面
平面 ?若存在,求线段
?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
 中,四边形
中,四边形 是正方形,
是正方形,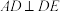 ,
,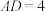 ,
,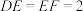 .
.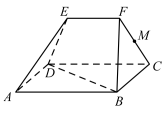
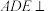 平面
平面 ;
;(2)设
 是
是 的中点,棱
的中点,棱 上是否存在点
上是否存在点 ,使得
,使得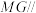 平面
平面 ?若存在,求线段
?若存在,求线段 的长;若不存在,说明理由.
的长;若不存在,说明理由.
您最近一年使用:0次
2021-04-28更新
|
1083次组卷
|
5卷引用:湖南省长沙市开福区长沙大学附属中学2024-2025学年高二上学期开学考试数学试题
湖南省长沙市开福区长沙大学附属中学2024-2025学年高二上学期开学考试数学试题河南省名校联盟2020-2021学年高三下学期4月联考(二) 数学(文科)试题(已下线)押第18题 立体几何-备战2021年高考数学(文)临考题号押题(全国卷1)(已下线)专题10 空间位置关系的判断与证明-2022年高考数学毕业班二轮热点题型归纳与变式演练(新高考专用)苏教版(2019) 必修第二册 过关斩将 第13章 专题强化练4 平面与平面的位置关系



