1 . 如图所示的多面体中,四边形ABCD是菱形且 ,
, ,
, 平面ABCD,
平面ABCD,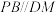 ,点N为PC上的动点.
,点N为PC上的动点.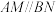 .
.
(2)求二面角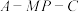 的正弦值.
的正弦值.
 ,
, ,
, 平面ABCD,
平面ABCD,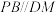 ,点N为PC上的动点.
,点N为PC上的动点.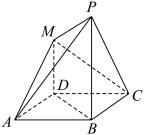
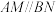 .
.(2)求二面角
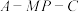 的正弦值.
的正弦值.
您最近一年使用:0次
2024-10-18更新
|
154次组卷
|
2卷引用:河南省南阳市内乡县夏关高中2024-2025学年高二上学期第二次阶段性测试数学试题
名校
2 . 如图,在棱长为2的正方体 中,
中, 为棱
为棱 的中点,
的中点, 为棱
为棱 的中点,平面
的中点,平面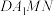 与平面
与平面 将该正方体截成三个多面体,其中
将该正方体截成三个多面体,其中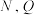 分别在棱
分别在棱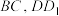 上.
上. 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
 中,
中, 为棱
为棱 的中点,
的中点, 为棱
为棱 的中点,平面
的中点,平面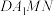 与平面
与平面 将该正方体截成三个多面体,其中
将该正方体截成三个多面体,其中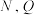 分别在棱
分别在棱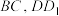 上.
上.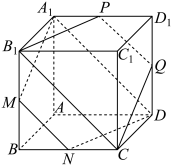
 平面
平面 ;
;(2)求异面直线
 与
与 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024-07-12更新
|
557次组卷
|
2卷引用:河南省鹤壁市高中2023-2024学年高一下学期7月期末考试数学试题
解题方法
3 . 如图,在四棱锥 中,
中,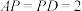 ,
,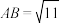 ,
,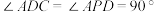 ,平面
,平面 平面ABCD.
平面ABCD. 平面PCD;
平面PCD;
(2)若E是棱PA的中点,且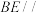 平面PCD,求异面直线BE与PD所成角的余弦值.
平面PCD,求异面直线BE与PD所成角的余弦值.
 中,
中,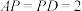 ,
,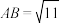 ,
,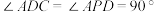 ,平面
,平面 平面ABCD.
平面ABCD.
 平面PCD;
平面PCD;(2)若E是棱PA的中点,且
 平面PCD,求异面直线BE与PD所成角的余弦值.
平面PCD,求异面直线BE与PD所成角的余弦值.
您最近一年使用:0次
2024-07-11更新
|
483次组卷
|
2卷引用:河南省开封市2023-2024学年高一下学期期末调研考试数学试题
名校
4 . 如图,三棱柱 中,面
中,面 面
面 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.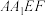 为平行四边形;
为平行四边形;
(2)若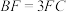 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,面
中,面 面
面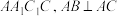 ,
, ,
, .过
.过 的平面交线段
的平面交线段 于点
于点 (不与端点重合),交线段
(不与端点重合),交线段 于点
于点 .
.
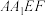 为平行四边形;
为平行四边形;(2)若
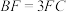 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
5 . 如图,空间六面体 中,
中,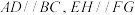 ,
,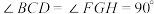 ,平面
,平面
 平面
平面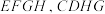 为正方形,平面
为正方形,平面 平面
平面 .
.

 ;
;
(2)若 ,求平面
,求平面 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 中,
中,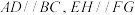 ,
,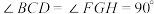 ,平面
,平面
 平面
平面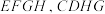 为正方形,平面
为正方形,平面 平面
平面 .
.


 ;
;(2)若
 ,求平面
,求平面 与平面
与平面 所成角的余弦值.
所成角的余弦值.
您最近一年使用:0次
2024-03-14更新
|
545次组卷
|
3卷引用:河南省焦作市博爱县第一中学2024届高三下学期4月月考数学试题
6 . 如图,在三棱锥 中,
中,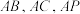 两两互相垂直,
两两互相垂直,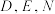 分别为棱
分别为棱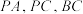 的中点,
的中点, 是线段
是线段 的中点,且
的中点,且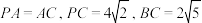
(1)求证: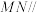 平面
平面 .
.
(2)在棱 上是否存在一点
上是否存在一点 ,使得直线
,使得直线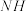 与平面
与平面 所成的角为
所成的角为 ,若存在,求线段
,若存在,求线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 中,
中,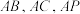 两两互相垂直,
两两互相垂直,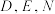 分别为棱
分别为棱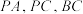 的中点,
的中点, 是线段
是线段 的中点,且
的中点,且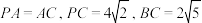

(1)求证:
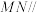 平面
平面 .
.(2)在棱
 上是否存在一点
上是否存在一点 ,使得直线
,使得直线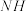 与平面
与平面 所成的角为
所成的角为 ,若存在,求线段
,若存在,求线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
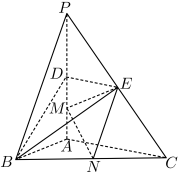
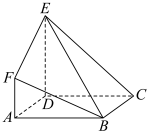
7 . 如图,在多面体 中,面
中,面 是正方形,
是正方形, 平面
平面 ,平面
,平面 平面
平面 ,
, ,
, ,
, ,
, 四点共面,
四点共面, ,
, .
. ;
;
(2)求点 到平面
到平面 的距离;
的距离;
(3)过点 与
与 垂直的平面交直线
垂直的平面交直线 于点
于点 ,求
,求 的长度.
的长度.
 中,面
中,面 是正方形,
是正方形, 平面
平面 ,平面
,平面 平面
平面 ,
, ,
, ,
, ,
, 四点共面,
四点共面, ,
, .
.
 ;
;(2)求点
 到平面
到平面 的距离;
的距离;(3)过点
 与
与 垂直的平面交直线
垂直的平面交直线 于点
于点 ,求
,求 的长度.
的长度.
您最近一年使用:0次
2023-04-25更新
|
1253次组卷
|
5卷引用:河南省信阳市宋基信阳实验中学2023-2024学年高二上学期教学测评(四)数学试题
河南省信阳市宋基信阳实验中学2023-2024学年高二上学期教学测评(四)数学试题北京市丰台区2023届高三二模数学试题北京卷专题20空间向量与立体几何(解答题)(已下线)每日一题 第6题 空间距离 要用向量(高二)(已下线)周测15 空间平行与垂直的关系(北京专版 )
8 . 在如图所示的六面体 中,平面
中,平面
 平面
平面 ,
, ,
, ,
, .
.
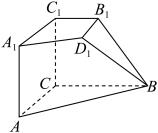
(1)求证:
 平面
平面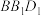 ;
;
(2)若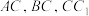 两两互相垂直,
两两互相垂直,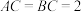 ,
,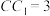 ,求二面角
,求二面角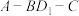 的余弦值.
的余弦值.
 中,平面
中,平面
 平面
平面 ,
,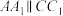 ,
,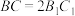 ,
, .
.
(1)求证:

 平面
平面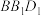 ;
;(2)若
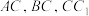 两两互相垂直,
两两互相垂直,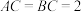 ,
,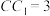 ,求二面角
,求二面角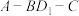 的余弦值.
的余弦值.
您最近一年使用:0次
2023-02-09更新
|
273次组卷
|
2卷引用:河南省濮阳市2022-2023学年高三下学期第一次摸底考试理科数学试题
解题方法
9 . 求证:夹在两个平行平面间的平行线段相等.画图,并用图中字母写出已知、求证;写出证明过程.
您最近一年使用:0次
2022-07-05更新
|
98次组卷
|
2卷引用:河南省许昌市2021-2022学年高一下学期期末数学理科试题
解题方法
10 . 如图所示,正方体 的棱长为3,
的棱长为3, 是棱
是棱 上的一个动点,
上的一个动点, 为
为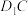 的中点.
的中点.
(1)求证:平面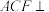 平面
平面 ;
;
(2)若 ,求证:
,求证: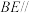 平面
平面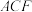 .
.
 的棱长为3,
的棱长为3, 是棱
是棱 上的一个动点,
上的一个动点, 为
为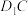 的中点.
的中点.
(1)求证:平面
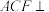 平面
平面 ;
;(2)若
 ,求证:
,求证: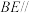 平面
平面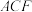 .
.
您最近一年使用:0次
2021-08-12更新
|
183次组卷
|
3卷引用:河南省焦作市普通高中2020-2021学年高二下学期期中考试试题文科数学



