名校
解题方法
1 . 已知双曲线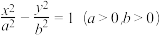
的离心率等于
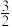，且点
在双曲线上.
(1)求双曲线的方程；
(2)若双曲线的左顶点为
，右焦点为
，P为双曲线右支上任意一点，求
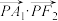的最小值.
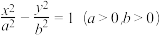的离心率等于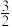，且点在双曲线上.(1)求双曲线的方程；
(2)若双曲线的左顶点为
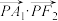，右焦点为，P为双曲线右支上任意一点，求的最小值.
您最近一年使用：0次
2022-03-27更新
|
2000次组卷
|
16卷引用：人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系
人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系江苏省徐州市沛县2020-2021学年高二上学期第一次学情调研数学试题北京市平谷区第五中学2020-2021学年高二上学期期中考试数学试题（已下线）3.2.2 双曲线的简单几何性质（2）-2020-2021学年高二数学课时同步练（人教A版选择性必修第一册）宁夏回族自治区银川一中2022届高三二模数学（文）试题宁夏回族自治区银川一中2022届高三二模数学（理）试题（已下线）3.2.1 双曲线的标准方程（课堂培优）-2021-2022学年高二数学课后培优练（苏教版2019选择性必修第一册）（已下线）3.2.2 双曲线的几何性质（课堂培优）-2021-2022学年高二数学课后培优练（苏教版2019选择性必修第一册）人教A版(2019) 选修第一册 实战演练 第三章 课时练习25 双曲线的简单几何性质安徽省六安市新安中学2021-2022学年高二上学期12月月考数学试题（已下线）专题3.8 双曲线的标准方程和性质-重难点题型检测-2021-2022学年高二数学举一反三系列（人教A版2019选择性必修第一册）（已下线）第06讲 双曲线 (精练）（已下线）第二章 平面解析几何之圆锥曲线的方程（A卷·知识通关练）（6）3.2.2 双曲线的几何性质（一）（同步练习基础版）广西玉林市博白第四高级中学2021-2022学年高二上学期期中数学（文）试题山东省威海市乳山市银滩高级中学2023-2024学年高二上学期12月月考数学试题
名校
解题方法
2 . （1）焦点在
轴上的椭圆过点
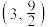，离心率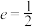
，求椭圆的标准方程；
（2）已知双曲线过点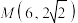
，它的渐近线方程为
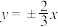，求双曲线的标准方程.
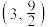轴上的椭圆过点，离心率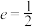，求椭圆的标准方程；（2）已知双曲线过点
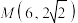，它的渐近线方程为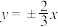，求双曲线的标准方程.
您最近一年使用：0次
2020-10-13更新
|
574次组卷
|
7卷引用：宁夏银川市第二中学2020-2021学年高二上学期月考（一）数学（理）试题
宁夏银川市第二中学2020-2021学年高二上学期月考（一）数学（理）试题宁夏银川市第二中学2020-2021学年高二上学期月考（一）数学（文）试题江苏省淮安市淮阴师范学院附属中学2020-2021学年高二上学期期中数学试题（已下线）第三章 圆锥曲线与方程B卷（综合培优）-【双基双测】2021-2022学年高二数学同步单元AB卷（苏教版2019选择性必修第一册）江苏省连云港市灌云县杨集高级中学2022-2023学年高二上学期第二次阶段检测数学试题山东省东营市利津县高级中学2023-2024学年高二上学期12月月考数学试题山东省东营市利津县2023-2024学年高二上学期12月阶段性检测数学试题
名校
解题方法
3 . 已知焦点在轴上的双曲线
经过点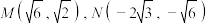
.
（1）求双曲线的离心率
；
（2）若直线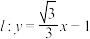
与双曲线交于
两点，求弦长
.
轴上的双曲线经过点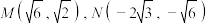.（1）求双曲线
的离心率；（2）若直线
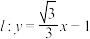与双曲线交于两点，求弦长.
您最近一年使用：0次
解题方法
4 . 求适合下列条件的双曲线的标准方程.
（1）焦点在x轴上，实轴长10，虚轴长8.
（2）焦点在y轴上，焦距是10，虚轴长8.
（3）离心率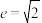
，经过点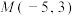
.
（1）焦点在x轴上，实轴长10，虚轴长8.
（2）焦点在y轴上，焦距是10，虚轴长8.
（3）离心率
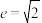，经过点.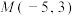
您最近一年使用：0次
2020-06-25更新
|
1239次组卷
|
5卷引用：宁夏贺兰县景博中学2019-2020学年高二上学期第一次月考数学试题
名校
5 . 求满足下列条件的曲线的方程：
（1）离心率为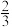
，长轴长为6的椭圆的标准方程
（2）与椭圆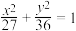
有相同焦点，且经过点
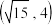的双曲线的标准方程．
（1）离心率为
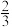，长轴长为6的椭圆的标准方程（2）与椭圆
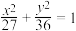有相同焦点，且经过点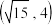的双曲线的标准方程．
您最近一年使用：0次
2020-01-02更新
|
488次组卷
|
4卷引用：宁夏回族自治区宁夏育才中学2019-2020学年高二上学期期中数学（文）试题
宁夏回族自治区宁夏育才中学2019-2020学年高二上学期期中数学（文）试题（已下线）专题2.3 双曲线-2020-2021学年高二数学课时同步练（苏教版选修1-1）宁夏青铜峡市高级中学2021-2022学年高二上学期期末考试数学（文）试题（已下线）专题2.3 双曲线-2020-2021学年高二数学课时同步练（苏教版选修2-1）
名校
6 . 已知双曲线
的中心在原点，对称轴为坐标轴，根据下列条件分别求双曲线的标准方程.
（1）渐近线方程为
，且过点
；
（2）与双曲线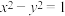
的离心率相同，与
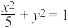共焦点.
的中心在原点，对称轴为坐标轴，根据下列条件分别求双曲线的标准方程. （1）渐近线方程为
，且过点；（2）与双曲线
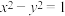的离心率相同，与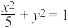共焦点.
您最近一年使用：0次
2019-01-18更新
|
395次组卷
|
2卷引用：宁夏育才中学2018-2019学年高二上学期期末考试数学（理）试题
