解题方法
1 . 已知双曲线E的两个焦点分别为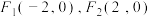 ,并且E经过点
,并且E经过点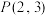 .
.
(1)求双曲线E的方程;
(2)过点 的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
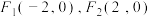 ,并且E经过点
,并且E经过点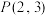 .
.(1)求双曲线E的方程;
(2)过点
 的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
的直线l与双曲线E有且仅有一个公共点,求直线l的方程.
您最近一年使用:0次
2023-08-24更新
|
988次组卷
|
16卷引用:福建省漳州市2019-2020学年高二上学期期末数学试题
福建省漳州市2019-2020学年高二上学期期末数学试题人教A版(2019) 选择性必修第一册 过关斩将 第三章 圆锥曲线的方程 专题强化练7 双曲线的综合运用辽宁省沈阳市东北育才外国语学校2023-2024学年高二上学期期中教学诊断数学试题(已下线)专题07 圆锥曲线的方程-双曲线的综合运用-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)人教A版(2019) 选修第一册 实战演练 第三章 课时练习26 直线与双曲线的位置关系河南省周口市太康县第三高级中学2022-2023学年高二上学期12月月考理数试题河南省周口市太康县第三高级中学2022-2023学年高二上学期12月月考文数试题新疆维吾尔自治区昌吉回族自治州2022-2023学年高二上学期11月期中质量检测数学试题(已下线)考点巩固卷21 双曲线方程及其性质(十一大考点)(已下线)考点15 直线与圆锥曲线相切问题 2024届高考数学考点总动员(已下线)第05讲 拓展二:直线与双曲线的位置关系(1)(已下线)3.2.2 双曲线的几何性质(1)(已下线)通关练16 双曲线13考点精练(100题)- 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)专题3.2 双曲线(5个考点十大题型)(2)【课后练】 3.2.2 双曲线的简单几何性质 课后作业-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程(已下线)重组8 高二期中真题重组卷(辽宁卷)A基础卷
解题方法
2 . 已知双曲线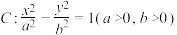 经过点
经过点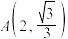 ,两个焦点为
,两个焦点为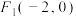 ,
,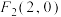 .
.
(1)求 的方程;
的方程;
(2)设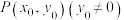 是
是 上一点,直线
上一点,直线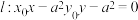 与直线
与直线 相交于点
相交于点 ,与直线
,与直线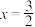 相交于点
相交于点 ,证明:当
,证明:当 点在
点在 上移动时,
上移动时,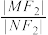 为定值,并求此定值.
为定值,并求此定值.
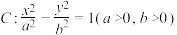 经过点
经过点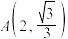 ,两个焦点为
,两个焦点为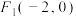 ,
,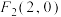 .
.(1)求
 的方程;
的方程;(2)设
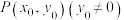 是
是 上一点,直线
上一点,直线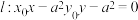 与直线
与直线 相交于点
相交于点 ,与直线
,与直线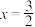 相交于点
相交于点 ,证明:当
,证明:当 点在
点在 上移动时,
上移动时,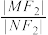 为定值,并求此定值.
为定值,并求此定值.
您最近一年使用:0次
3 . 双曲线 的左、右焦点分别为
的左、右焦点分别为 、
、 ,点
,点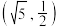 ,
,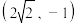 在双曲线
在双曲线 上.
上.
(1)求双曲线 的标准方程;
的标准方程;
(2)直线 过点
过点 且与双曲线
且与双曲线 交于
交于 、
、 两点,且
两点,且 的中点的横坐标为
的中点的横坐标为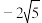 ,求直线
,求直线 的方程.
的方程.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,点
,点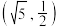 ,
,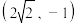 在双曲线
在双曲线 上.
上.(1)求双曲线
 的标准方程;
的标准方程;(2)直线
 过点
过点 且与双曲线
且与双曲线 交于
交于 、
、 两点,且
两点,且 的中点的横坐标为
的中点的横坐标为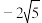 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2019-11-28更新
|
878次组卷
|
2卷引用:河南省开封市五县联考2019-2020学年高二上学期期中数学(理)试题
4 . 已知双曲线方程为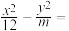 1,双曲线的一支上不同的三点A(x1,y1),B(6,
1,双曲线的一支上不同的三点A(x1,y1),B(6,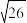 ),C(x2,y2)到焦点F(5,0)的距离成等差数列.
),C(x2,y2)到焦点F(5,0)的距离成等差数列.
(1)求m的值;
(2)试求x1+x2的值.
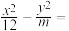 1,双曲线的一支上不同的三点A(x1,y1),B(6,
1,双曲线的一支上不同的三点A(x1,y1),B(6,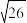 ),C(x2,y2)到焦点F(5,0)的距离成等差数列.
),C(x2,y2)到焦点F(5,0)的距离成等差数列.(1)求m的值;
(2)试求x1+x2的值.
您最近一年使用:0次
11-12高二·辽宁沈阳·期末
名校
5 . 双曲线 :
: 上一点
上一点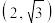 到左,右两焦点距离的差为
到左,右两焦点距离的差为 .
.
(1)求双曲线的方程;
(2)设 ,
, 是双曲线的左右焦点,
是双曲线的左右焦点, 是双曲线上的点,若
是双曲线上的点,若 ,
,
求 的面积;
的面积;
(3)过 作直线
作直线 交双曲线
交双曲线 于
于 ,
, 两点,若
两点,若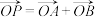 ,是否存在这样的直线
,是否存在这样的直线 ,使
,使 为矩形?若存在,求出
为矩形?若存在,求出 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
 :
: 上一点
上一点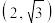 到左,右两焦点距离的差为
到左,右两焦点距离的差为 .
.(1)求双曲线的方程;
(2)设
 ,
, 是双曲线的左右焦点,
是双曲线的左右焦点, 是双曲线上的点,若
是双曲线上的点,若 ,
,求
 的面积;
的面积;(3)过
 作直线
作直线 交双曲线
交双曲线 于
于 ,
, 两点,若
两点,若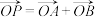 ,是否存在这样的直线
,是否存在这样的直线 ,使
,使 为矩形?若存在,求出
为矩形?若存在,求出 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
您最近一年使用:0次



