名校
解题方法
1 . 已知双曲线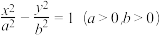 的离心率等于
的离心率等于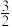 ,且点
,且点 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若双曲线的左顶点为 ,右焦点为
,右焦点为 ,P为双曲线右支上任意一点,求
,P为双曲线右支上任意一点,求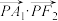 的最小值.
的最小值.
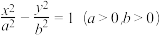 的离心率等于
的离心率等于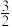 ,且点
,且点 在双曲线上.
在双曲线上.(1)求双曲线的方程;
(2)若双曲线的左顶点为
 ,右焦点为
,右焦点为 ,P为双曲线右支上任意一点,求
,P为双曲线右支上任意一点,求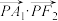 的最小值.
的最小值.
您最近一年使用:0次
2022-03-27更新
|
2065次组卷
|
16卷引用:人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系
人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.8 直线与圆锥曲线的位置关系江苏省徐州市沛县2020-2021学年高二上学期第一次学情调研数学试题北京市平谷区第五中学2020-2021学年高二上学期期中考试数学试题(已下线)3.2.2 双曲线的简单几何性质(2)-2020-2021学年高二数学课时同步练(人教A版选择性必修第一册)安徽省六安市新安中学2021-2022学年高二上学期12月月考数学试题(已下线)3.2.1 双曲线的标准方程(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)(已下线)3.2.2 双曲线的几何性质(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)人教A版(2019) 选修第一册 实战演练 第三章 课时练习25 双曲线的简单几何性质(已下线)专题3.8 双曲线的标准方程和性质-重难点题型检测-2021-2022学年高二数学举一反三系列(人教A版2019选择性必修第一册)宁夏回族自治区银川一中2022届高三二模数学(文)试题宁夏回族自治区银川一中2022届高三二模数学(理)试题(已下线)第06讲 双曲线 (精练)(已下线)第二章 平面解析几何之圆锥曲线的方程(A卷·知识通关练)(6)3.2.2 双曲线的几何性质(一)(同步练习基础版)广西玉林市博白第四高级中学2021-2022学年高二上学期期中数学(文)试题山东省威海市乳山市银滩高级中学2023-2024学年高二上学期12月月考数学试题
20-21高二·全国·单元测试
名校
解题方法
2 . 根据下列条件,求双曲线的标准方程.
(1)焦距为 ,经过点
,经过点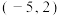 ,且焦点在
,且焦点在 轴上;
轴上;
(2)焦点为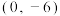 ,
,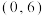 ,且过点
,且过点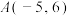 .
.
(1)焦距为
 ,经过点
,经过点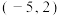 ,且焦点在
,且焦点在 轴上;
轴上;(2)焦点为
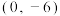 ,
,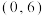 ,且过点
,且过点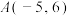 .
.
您最近一年使用:0次
2021-11-30更新
|
333次组卷
|
6卷引用:专题17 双曲线及其标准方程(核心素养练习)-【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第一册)
(已下线)专题17 双曲线及其标准方程(核心素养练习)-【新教材精创】2020-2021学年高二数学新教材知识讲学(人教A版选择性必修第一册)安徽省安庆市第七中学2021-2022学年高二上学期12月阶段性考试数学试题(已下线)3.2 双曲线-2021-2022学年高二数学尖子生同步培优题典(苏教版2019选择性必修第一册)(已下线)3.2.1双曲线的标准方程(备作业)-【上好课】-2021-2022学年高二数学同步备课系列(苏教版2019必修第一册)(已下线)第3.3讲 双曲线及其标准方程-2021-2022学年高二数学链接教材精准变式练(人教A版2019选择性必修第一册)【典例题】 3.2.1.1 双曲线的标准方程 课堂例题-湘教版(2019)选择性必修第一册 第3章 圆锥曲线与方程
解题方法
3 . 已知中心在原点,焦点在坐标轴上的双曲线 经过
经过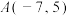 ,
,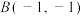 两点.
两点.
(1)求双曲线 的方程;
的方程;
(2)设直线 :
: 交双曲线
交双曲线 于
于 ,
, 两点,且线段
两点,且线段 被圆
被圆 :
: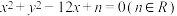 三等分,求实数
三等分,求实数 ,
, 的值.
的值.
 经过
经过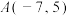 ,
,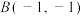 两点.
两点.(1)求双曲线
 的方程;
的方程;(2)设直线
 :
: 交双曲线
交双曲线 于
于 ,
, 两点,且线段
两点,且线段 被圆
被圆 :
: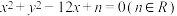 三等分,求实数
三等分,求实数 ,
, 的值.
的值.
您最近一年使用:0次
名校
解题方法
4 . 求曲线(中心在原点,焦点在坐标轴上)方程:
(1)若椭圆经过点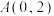 和
和 ,求椭圆标准方程.
,求椭圆标准方程.
(2)若双曲线经过点 ,且它的两条渐近线方程是
,且它的两条渐近线方程是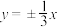 ,求双曲线的标准方程.
,求双曲线的标准方程.
(1)若椭圆经过点
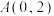 和
和 ,求椭圆标准方程.
,求椭圆标准方程.(2)若双曲线经过点
 ,且它的两条渐近线方程是
,且它的两条渐近线方程是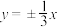 ,求双曲线的标准方程.
,求双曲线的标准方程.
您最近一年使用:0次
名校
解题方法
5 . 已知双曲线 与椭圆
与椭圆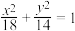 有共同的焦点,点
有共同的焦点,点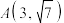 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程及渐近线方程;
(2)以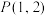 为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
 与椭圆
与椭圆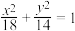 有共同的焦点,点
有共同的焦点,点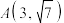 在双曲线C上.
在双曲线C上.(1)求双曲线C的方程及渐近线方程;
(2)以
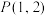 为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
为中点作双曲线C的一条弦AB,求弦AB所在直线的方程.
您最近一年使用:0次
2020-11-04更新
|
3959次组卷
|
10卷引用:浙江省金华市曙光学校2020-2021学年高二上学期第一次阶段考试数学试题
浙江省金华市曙光学校2020-2021学年高二上学期第一次阶段考试数学试题安徽省合肥市庐江县第五中学(庐巢八校联考)2022-2023学年高二上学期12月月考数学试题吉林省长春市第二十九中学2020-2021学年高二上学期期末考试数学(文)试题云南省曲靖市沾益区第四中学2020-2021学年高二5月月考数学(理)试题人教A版(2019) 选修第一册 实战演练 第三章 验收检测圆锥曲线之间的综合问题河南省南阳市第六完全学校高级中学2022-2023学年高二上学期10月月考数学试题黑龙江省哈尔滨市宾县第二中学2022-2023学年高二上学期期中考试数学试题湖南省株洲市攸县健坤高级中学2023-2024学年高二上学期第三次月考数学试题内蒙古自治区兴安盟乌兰浩特第二中学2025届高三上学期开学摸底考试数学试卷
名校
解题方法
6 . 已知双曲线 :
: 的离心率为
的离心率为 ,且过点
,且过点 .
.
(1)求双曲线 的方程;
的方程;
(2)若直线 :
: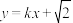 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 ,
, ,求
,求 的取值范围.
的取值范围.
 :
: 的离心率为
的离心率为 ,且过点
,且过点 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
 :
: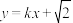 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 ,
, ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-08-04更新
|
707次组卷
|
5卷引用:安徽省滁州市定远县育才学校2019-2020学年高二下学期期末数学(文)试题
安徽省滁州市定远县育才学校2019-2020学年高二下学期期末数学(文)试题(已下线)第三章 圆锥曲线的方程+章末测试-2020-2021学年一隅三反系列之高二数学新教材选择性必修第一册(人教A版)河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第3次能力达标理科数学试题河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第三次能力达标检测文科数学试题河南省洛阳市宜阳第一高级中学2022-2023学年高二上学期第三次月考数学试题(文)
名校
解题方法
7 . 已知双曲线的焦点为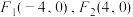 ,且该双曲线过点
,且该双曲线过点 .
.
(1)求双曲线的标准方程;
(2)若双曲线上的点 满足
满足 ,求
,求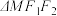 的面积.
的面积.
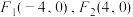 ,且该双曲线过点
,且该双曲线过点 .
.(1)求双曲线的标准方程;
(2)若双曲线上的点
 满足
满足 ,求
,求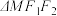 的面积.
的面积.
您最近一年使用:0次
2020-03-16更新
|
333次组卷
|
5卷引用:湖北省荆门市2019-2020学年高二上学期期末数学试题
名校
解题方法
8 . 分别求出满合下列条件的圆锥曲线的标准方程:
(1)离心率为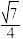 ,且短轴长为6的椭圆
,且短轴长为6的椭圆 ;
;
(2)过点 ,且与椭圆
,且与椭圆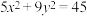 有相同焦点的双曲线
有相同焦点的双曲线 .
.
(1)离心率为
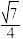 ,且短轴长为6的椭圆
,且短轴长为6的椭圆 ;
;(2)过点
 ,且与椭圆
,且与椭圆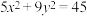 有相同焦点的双曲线
有相同焦点的双曲线 .
.
您最近一年使用:0次
2020-03-05更新
|
467次组卷
|
2卷引用:安徽省凤阳县第二中学2019-2020学年高二上学期期末考试数学(文)试题
名校
9 . 已知椭圆C的中心在原点,焦点在x轴上,且长轴长为12,离心率为 .
.
(1)求椭圆C的标准方程;
(2)已知双曲线E过点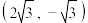 ,且双曲线E的焦点与椭圆C的焦点重合,求双曲线E的标准方程.
,且双曲线E的焦点与椭圆C的焦点重合,求双曲线E的标准方程.
 .
.(1)求椭圆C的标准方程;
(2)已知双曲线E过点
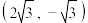 ,且双曲线E的焦点与椭圆C的焦点重合,求双曲线E的标准方程.
,且双曲线E的焦点与椭圆C的焦点重合,求双曲线E的标准方程.
您最近一年使用:0次
2020-02-26更新
|
403次组卷
|
6卷引用:陕西省西安市2019-2020学年高二上学期期末数学(文)试题
陕西省西安市2019-2020学年高二上学期期末数学(文)试题陕西省西安市2019-2020学年高二上学期期末数学(理)试题陕西省西安市远东一中2019-2020学年高二上学期期末数学(理)试题安徽省皖南十校2022-2023学年高二上学期期末文科数学试题(已下线)专题12 双曲线-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练沪教版(2020) 选修第一册 单元训练 第2章 双曲线(A卷)
10 . (1)点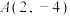 在以原点为顶点,坐标轴为对称轴的抛物线上,求抛物线方程;
在以原点为顶点,坐标轴为对称轴的抛物线上,求抛物线方程;
(2)已知双曲线C经过点 ,它的一条渐近线方程为
,它的一条渐近线方程为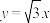 ,求双曲线C的标准方程.
,求双曲线C的标准方程.
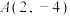 在以原点为顶点,坐标轴为对称轴的抛物线上,求抛物线方程;
在以原点为顶点,坐标轴为对称轴的抛物线上,求抛物线方程;(2)已知双曲线C经过点
 ,它的一条渐近线方程为
,它的一条渐近线方程为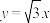 ,求双曲线C的标准方程.
,求双曲线C的标准方程.
您最近一年使用:0次
2020-04-30更新
|
18次组卷
|
2卷引用:安徽省滁州市定远县第二中学2018-2019学年高二上学期第三次调研考试数学(文)试题



