解题方法
1 . 已知动点M到定点 的距离比点M到定直线
的距离比点M到定直线 的距离小1.
的距离小1.
(1)求点M的轨迹C的方程.
(2)过点F作两条互相垂直的直线 和
和 ,分别交曲线C于点A,B和K,N.设线段AB,KN的中点分别为P,Q,求证:直线
,分别交曲线C于点A,B和K,N.设线段AB,KN的中点分别为P,Q,求证:直线 恒过一个定点.
恒过一个定点.
 的距离比点M到定直线
的距离比点M到定直线 的距离小1.
的距离小1.(1)求点M的轨迹C的方程.
(2)过点F作两条互相垂直的直线
 和
和 ,分别交曲线C于点A,B和K,N.设线段AB,KN的中点分别为P,Q,求证:直线
,分别交曲线C于点A,B和K,N.设线段AB,KN的中点分别为P,Q,求证:直线 恒过一个定点.
恒过一个定点.
您最近一年使用:0次
2 . 平面直角坐标系 中,过点
中,过点 的动直线l与抛物线
的动直线l与抛物线 交于A,B两点且
交于A,B两点且 .
.
(1)求t的值;
(2)若点M在x轴上且 ,在x轴上是否存在确定的点P,使得当动直线l不与x轴垂直时,恒有
,在x轴上是否存在确定的点P,使得当动直线l不与x轴垂直时,恒有 .若存在,请求出点P的坐标:若不存在,请说明理由.
.若存在,请求出点P的坐标:若不存在,请说明理由.
 中,过点
中,过点 的动直线l与抛物线
的动直线l与抛物线 交于A,B两点且
交于A,B两点且 .
.(1)求t的值;
(2)若点M在x轴上且
 ,在x轴上是否存在确定的点P,使得当动直线l不与x轴垂直时,恒有
,在x轴上是否存在确定的点P,使得当动直线l不与x轴垂直时,恒有 .若存在,请求出点P的坐标:若不存在,请说明理由.
.若存在,请求出点P的坐标:若不存在,请说明理由.
您最近一年使用:0次
3 . 若抛物线 的焦点为
的焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且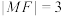 .
.
(1)求抛物线
 的方程;
的方程;(2)过点
 的直线
的直线 交抛物线
交抛物线 于
于 两点,点A关于
两点,点A关于 轴的对称点是
轴的对称点是 ,证明:
,证明: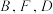 三点共线.
三点共线.
您最近一年使用:0次
解题方法
4 . 已知抛物线 ,
, 是
是 上一点.
上一点.
(1)求证:直线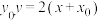 与
与 相切;
相切;
(2)设过点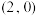 的直线
的直线 与
与 交于
交于 ,
, 两点,分别过
两点,分别过 ,
, 作
作 的切线
的切线 ,
, ,
, 与
与 相交于点
相交于点 ,求证:点
,求证:点 在定直线上.
在定直线上.
 ,
, 是
是 上一点.
上一点.(1)求证:直线
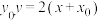 与
与 相切;
相切;(2)设过点
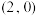 的直线
的直线 与
与 交于
交于 ,
, 两点,分别过
两点,分别过 ,
, 作
作 的切线
的切线 ,
, ,
, 与
与 相交于点
相交于点 ,求证:点
,求证:点 在定直线上.
在定直线上.
您最近一年使用:0次
解题方法
5 . 已知抛物线 的焦点为
的焦点为 ,且点
,且点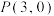 关于直线
关于直线 的对称点恰好在
的对称点恰好在 上.
上.
(1)求抛物线 的方程;
的方程;
(2)斜率为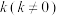 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且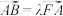 ,过点
,过点 且与直线
且与直线 垂直的直线交
垂直的直线交 轴于点
轴于点 ,求证:
,求证: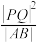 为定值,并求出该定值.
为定值,并求出该定值.
 的焦点为
的焦点为 ,且点
,且点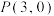 关于直线
关于直线 的对称点恰好在
的对称点恰好在 上.
上.(1)求抛物线
 的方程;
的方程;(2)斜率为
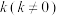 的直线
的直线 与抛物线
与抛物线 交于
交于 两点,且
两点,且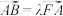 ,过点
,过点 且与直线
且与直线 垂直的直线交
垂直的直线交 轴于点
轴于点 ,求证:
,求证: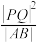 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
名校
解题方法
6 . 已知抛物线 与
与 交于
交于 两点,其中点
两点,其中点 在第一象限,且
在第一象限,且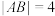 ,抛物线
,抛物线 的准线
的准线 与
与 轴交于点
轴交于点 .
.
(1)求以线段 为直径的圆的方程;
为直径的圆的方程;
(2)若 在抛物线
在抛物线 上,且
上,且 ,探究:直线
,探究:直线 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
 与
与 交于
交于 两点,其中点
两点,其中点 在第一象限,且
在第一象限,且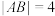 ,抛物线
,抛物线 的准线
的准线 与
与 轴交于点
轴交于点 .
.(1)求以线段
 为直径的圆的方程;
为直径的圆的方程;(2)若
 在抛物线
在抛物线 上,且
上,且 ,探究:直线
,探究:直线 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
您最近一年使用:0次
2024-02-25更新
|
645次组卷
|
2卷引用:1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(文科)试题(十九)
解题方法
7 . 已知 为抛物线
为抛物线 的焦点,直线
的焦点,直线 交抛物线
交抛物线 于
于 ,
, 两点,
两点,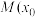 ,
, 为
为 的中点,且
的中点,且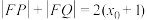 .
.
(1)求抛物线
 的方程;
的方程;(2)经过点(12,8)的两条直线
 的斜率分别为
的斜率分别为 ,且
,且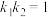 ,若直线
,若直线 交抛物线于点
交抛物线于点 ,直线
,直线 交抛物线于点
交抛物线于点 ,线段
,线段 和
和 的中点分别为
的中点分别为 ,
, .试判断直线
.试判断直线 是否经过定点,若经过求出定点;若不经过,说明理由.
是否经过定点,若经过求出定点;若不经过,说明理由.
您最近一年使用:0次
2024-02-21更新
|
110次组卷
|
2卷引用:中原名校2022年高三上学期第四次精英联赛理科数学试题
8 . 若抛物线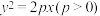 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 交抛物线于
交抛物线于 .
.
(1)当 平行于
平行于 轴时,
轴时,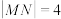 ,求
,求 ;
;
(2)当 时,现有以下两个结论:①
时,现有以下两个结论:①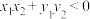 ;②
;②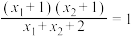 .请选择其中一个结论证明.
.请选择其中一个结论证明.
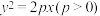 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 交抛物线于
交抛物线于 .
.(1)当
 平行于
平行于 轴时,
轴时,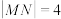 ,求
,求 ;
;(2)当
 时,现有以下两个结论:①
时,现有以下两个结论:①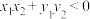 ;②
;②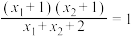 .请选择其中一个结论证明.
.请选择其中一个结论证明.
您最近一年使用:0次
名校
解题方法
9 . 已知焦点为 的抛物线
的抛物线 :
: (
( )上一点
)上一点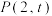 到
到 的距离是4.
的距离是4.
(1)求抛物线 的方程.
的方程.
(2)若不过原点 的直线
的直线 与抛物线
与抛物线 交于
交于 ,
, 两点(
两点( ,
, 位于
位于 轴两侧),
轴两侧), 的准线
的准线 与
与 轴交于点
轴交于点 ,直线
,直线 ,
, 与
与 分别交于点
分别交于点 ,
, ,若
,若 ,证明:直线
,证明:直线 过定点.
过定点.
 的抛物线
的抛物线 :
: (
( )上一点
)上一点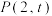 到
到 的距离是4.
的距离是4.(1)求抛物线
 的方程.
的方程.(2)若不过原点
 的直线
的直线 与抛物线
与抛物线 交于
交于 ,
, 两点(
两点( ,
, 位于
位于 轴两侧),
轴两侧), 的准线
的准线 与
与 轴交于点
轴交于点 ,直线
,直线 ,
, 与
与 分别交于点
分别交于点 ,
, ,若
,若 ,证明:直线
,证明:直线 过定点.
过定点.
您最近一年使用:0次
2024-01-10更新
|
553次组卷
|
2卷引用:陕西省西安博爱国际学校2021-2022学年高二上学期期末理科数学试题
10 . 已知抛物线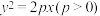 的焦点为
的焦点为 ,点
,点 为坐标原点,线段
为坐标原点,线段 的垂直平分线交抛物线于
的垂直平分线交抛物线于 两点,
两点,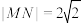 .
.
(1)求抛物线的标准方程;
(2)点 是抛物线上异于点
是抛物线上异于点 的两个动点,且
的两个动点,且 ,求证:直线
,求证:直线 恒过一定点.
恒过一定点.
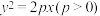 的焦点为
的焦点为 ,点
,点 为坐标原点,线段
为坐标原点,线段 的垂直平分线交抛物线于
的垂直平分线交抛物线于 两点,
两点,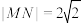 .
.(1)求抛物线的标准方程;
(2)点
 是抛物线上异于点
是抛物线上异于点 的两个动点,且
的两个动点,且 ,求证:直线
,求证:直线 恒过一定点.
恒过一定点.
您最近一年使用:0次



