1 . 在平面直角坐标系 中,P,Q是抛物线
中,P,Q是抛物线 上两点(异于点O),过点P且与C相切的直线l交x轴于点M,且直线
上两点(异于点O),过点P且与C相切的直线l交x轴于点M,且直线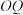 与l的斜率乘积为
与l的斜率乘积为 .
.
(1)求证:直线 过定点,并求此定点D的坐标;
过定点,并求此定点D的坐标;
(2)过M作l的垂线交椭圆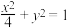 于A,B两点,过D作l的平行线交直线
于A,B两点,过D作l的平行线交直线 于H,记
于H,记 的面积为S,
的面积为S, 的面积为T.
的面积为T.
①当 取最大值时,求点P的纵坐标;
取最大值时,求点P的纵坐标;
②证明:存在定点G,使 为定值.
为定值.
 中,P,Q是抛物线
中,P,Q是抛物线 上两点(异于点O),过点P且与C相切的直线l交x轴于点M,且直线
上两点(异于点O),过点P且与C相切的直线l交x轴于点M,且直线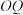 与l的斜率乘积为
与l的斜率乘积为 .
.(1)求证:直线
 过定点,并求此定点D的坐标;
过定点,并求此定点D的坐标;(2)过M作l的垂线交椭圆
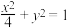 于A,B两点,过D作l的平行线交直线
于A,B两点,过D作l的平行线交直线 于H,记
于H,记 的面积为S,
的面积为S, 的面积为T.
的面积为T.①当
 取最大值时,求点P的纵坐标;
取最大值时,求点P的纵坐标;②证明:存在定点G,使
 为定值.
为定值.
您最近一年使用:0次
2023-05-08更新
|
996次组卷
|
5卷引用:湖南省株洲市第二中学2022届高三下学期第三次月考数学试题
湖南省株洲市第二中学2022届高三下学期第三次月考数学试题山东省烟台市2023届高考适应性练习(一)数学试题山东省枣庄市2023届高三三模数学试题(已下线)高二上学期期中复习【第三章 圆锥曲线的方程】十二大题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)通关练17 抛物线8考点精练(3)
2 . 已知 的一个顶点为抛物线
的一个顶点为抛物线 的顶点O,
的顶点O, 两点都在抛物线上,且
两点都在抛物线上,且 .
.
(1)求证:直线 必过一定点;
必过一定点;
(2)求 面积的最小值.
面积的最小值.
 的一个顶点为抛物线
的一个顶点为抛物线 的顶点O,
的顶点O, 两点都在抛物线上,且
两点都在抛物线上,且 .
.(1)求证:直线
 必过一定点;
必过一定点;(2)求
 面积的最小值.
面积的最小值.
您最近一年使用:0次
3 . 已知抛物线H:x2=2py(p>0)的焦点为F,过点(0,1)作倾斜角为45°的直线交H于A,B两点,且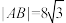 .
.
(1)求抛物线H的方程;
(2)设直线l的方程为 ,且l与H相交于C,D两点,若以CD为直径的圆G恰好经过点F,求圆G的面积.
,且l与H相交于C,D两点,若以CD为直径的圆G恰好经过点F,求圆G的面积.
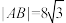 .
.(1)求抛物线H的方程;
(2)设直线l的方程为
 ,且l与H相交于C,D两点,若以CD为直径的圆G恰好经过点F,求圆G的面积.
,且l与H相交于C,D两点,若以CD为直径的圆G恰好经过点F,求圆G的面积.
您最近一年使用:0次
2023-02-26更新
|
366次组卷
|
2卷引用:湖南省长沙市雅礼中学2022-2023学年高三上学期月考(四)数学试题
名校
解题方法
4 . 已知抛物线 上一点
上一点 到焦点
到焦点 的距离为4.
的距离为4.
(1)求抛物线 的标准方程;
的标准方程;
(2)过焦点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,
, ,
, 为坐标原点,设直线
为坐标原点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 上一点
上一点 到焦点
到焦点 的距离为4.
的距离为4.(1)求抛物线
 的标准方程;
的标准方程;(2)过焦点
 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,
, ,
, 为坐标原点,设直线
为坐标原点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2022-12-20更新
|
617次组卷
|
5卷引用:湖南省郴州市嘉禾县第六中学2022-2023学年高二上学期第三次月考数学试题
解题方法
5 . 若抛物线 :
: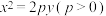 上的一点
上的一点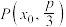 到它的焦点的距离为
到它的焦点的距离为 .
.
(1)求C的标准方程;
(2)若过点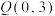 的直线
的直线 与抛物线C相交于A,B两点.求证:
与抛物线C相交于A,B两点.求证: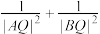 为定值.
为定值.
 :
: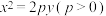 上的一点
上的一点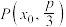 到它的焦点的距离为
到它的焦点的距离为 .
.(1)求C的标准方程;
(2)若过点
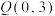 的直线
的直线 与抛物线C相交于A,B两点.求证:
与抛物线C相交于A,B两点.求证: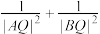 为定值.
为定值.
您最近一年使用:0次
解题方法
6 . 已知抛物线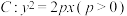 ,过点
,过点 作直线与
作直线与 交于
交于 ,
, 两点,当该直线垂直于
两点,当该直线垂直于 轴时,
轴时, 的面积为2,其中
的面积为2,其中 为坐标原点.
为坐标原点.
(1)求 的方程.
的方程.
(2)若 的一条弦
的一条弦 经过
经过 的焦点,且直线
的焦点,且直线 与直线
与直线 平行,试问是否存在常数
平行,试问是否存在常数 ,使得
,使得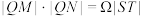 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
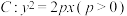 ,过点
,过点 作直线与
作直线与 交于
交于 ,
, 两点,当该直线垂直于
两点,当该直线垂直于 轴时,
轴时, 的面积为2,其中
的面积为2,其中 为坐标原点.
为坐标原点.(1)求
 的方程.
的方程.(2)若
 的一条弦
的一条弦 经过
经过 的焦点,且直线
的焦点,且直线 与直线
与直线 平行,试问是否存在常数
平行,试问是否存在常数 ,使得
,使得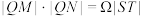 恒成立?若存在,求
恒成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2022-11-26更新
|
626次组卷
|
8卷引用:湖南省部分学校2022-2023学年高三上学期12月联考数学试题
解题方法
7 . 在直角坐标系 中,已知抛物线
中,已知抛物线 ,
, 为直线
为直线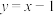 上的动点,过点
上的动点,过点 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为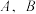 ,当
,当 在
在 轴上时,
轴上时, .
.
(1)求抛物线 的方程;
的方程;
(2)求点 到直线
到直线 距离的最大值.
距离的最大值.
 中,已知抛物线
中,已知抛物线 ,
, 为直线
为直线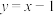 上的动点,过点
上的动点,过点 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为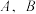 ,当
,当 在
在 轴上时,
轴上时, .
.(1)求抛物线
 的方程;
的方程;(2)求点
 到直线
到直线 距离的最大值.
距离的最大值.
您最近一年使用:0次
名校
解题方法
8 . 已知抛物线 与直线
与直线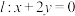 交于M,N两点,且线段MN的中点为
交于M,N两点,且线段MN的中点为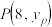 .
.
(1)求抛物线C的方程;
(2)过点P作直线m交抛物线于点A,B,是否存在定点M,使得以弦AB为直径的圆恒过点M.若存在,请求出点M坐标;若不存在,请说明理由.
 与直线
与直线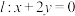 交于M,N两点,且线段MN的中点为
交于M,N两点,且线段MN的中点为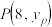 .
.(1)求抛物线C的方程;
(2)过点P作直线m交抛物线于点A,B,是否存在定点M,使得以弦AB为直径的圆恒过点M.若存在,请求出点M坐标;若不存在,请说明理由.
您最近一年使用:0次
2022-10-12更新
|
644次组卷
|
3卷引用:湖南省长沙市周南中学2022-2023学年高三上学期第二次月考数学试题
名校
9 . 在平面直角坐标系中,抛物线 与
与 轴分别相交于
轴分别相交于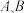 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 ,设抛物线
,设抛物线 的对称轴与
的对称轴与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求 的值;
的值;
(2)将抛物线 向上平移3个单位,得到抛物线
向上平移3个单位,得到抛物线 ,设点
,设点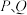 是抛物线
是抛物线 上在第一象限内不同的两点,射线
上在第一象限内不同的两点,射线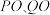 分别交直线
分别交直线 于点
于点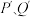 ,设
,设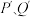 的横坐标分别为
的横坐标分别为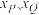 ,且
,且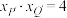 ,求证:直线
,求证:直线 经过定点.
经过定点.
 与
与 轴分别相交于
轴分别相交于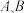 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴相交于点
轴相交于点 ,设抛物线
,设抛物线 的对称轴与
的对称轴与 轴相交于点
轴相交于点 ,且
,且 .
.(1)求
 的值;
的值;(2)将抛物线
 向上平移3个单位,得到抛物线
向上平移3个单位,得到抛物线 ,设点
,设点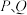 是抛物线
是抛物线 上在第一象限内不同的两点,射线
上在第一象限内不同的两点,射线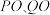 分别交直线
分别交直线 于点
于点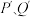 ,设
,设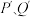 的横坐标分别为
的横坐标分别为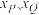 ,且
,且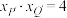 ,求证:直线
,求证:直线 经过定点.
经过定点.
您最近一年使用:0次
10 . 已知抛物线C: (
( ),直线
),直线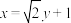 交抛物线C于A,B两点,且三角形OAB的面积为
交抛物线C于A,B两点,且三角形OAB的面积为 (O为坐标原点).
(O为坐标原点).
(1)求实数p的值;
(2)过点D(2,0)作直线L交抛物线C于P,Q两点,点P关于x轴的对称点为P'.证明:直线P'Q经过定点,并求出定点坐标.
 (
( ),直线
),直线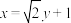 交抛物线C于A,B两点,且三角形OAB的面积为
交抛物线C于A,B两点,且三角形OAB的面积为 (O为坐标原点).
(O为坐标原点).(1)求实数p的值;
(2)过点D(2,0)作直线L交抛物线C于P,Q两点,点P关于x轴的对称点为P'.证明:直线P'Q经过定点,并求出定点坐标.
您最近一年使用:0次
2022-07-17更新
|
916次组卷
|
3卷引用:湖南省长沙市第一中学2023届高三上学期入学摸底考试数学试题



