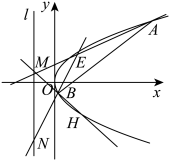
1 . 如图,点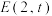 为抛物线
为抛物线 上位于第一象限的一点,F为抛物线焦点,满足
上位于第一象限的一点,F为抛物线焦点,满足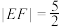 .
.
(1)求抛物线C的方程;
(2)点M为直线 上的动点,H为点E关于x轴的对称点,连接
上的动点,H为点E关于x轴的对称点,连接 、
、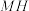 分别交C于点A、B,连接
分别交C于点A、B,连接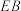 交直线l于点N.
交直线l于点N.
①求证:直线 过定点;
过定点;
②求证:以 为直径的圆过定点.
为直径的圆过定点.
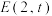 为抛物线
为抛物线 上位于第一象限的一点,F为抛物线焦点,满足
上位于第一象限的一点,F为抛物线焦点,满足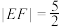 .
.
(1)求抛物线C的方程;
(2)点M为直线
 上的动点,H为点E关于x轴的对称点,连接
上的动点,H为点E关于x轴的对称点,连接 、
、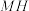 分别交C于点A、B,连接
分别交C于点A、B,连接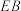 交直线l于点N.
交直线l于点N.①求证:直线
 过定点;
过定点;②求证:以
 为直径的圆过定点.
为直径的圆过定点.
您最近一年使用:0次
解题方法
2 . 如图,抛物线 在点
在点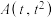 (
( )处的切线
)处的切线 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 (
( 的倾斜角与
的倾斜角与 的倾斜角互补)交抛物线于
的倾斜角互补)交抛物线于 ,
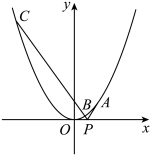
, 两点,求证:
两点,求证:
(1) 的斜率为
的斜率为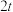 ;
;
(2)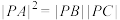 .
.
 在点
在点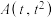 (
( )处的切线
)处的切线 交
交 轴于点
轴于点 ,过点
,过点 作直线
作直线 (
( 的倾斜角与
的倾斜角与 的倾斜角互补)交抛物线于
的倾斜角互补)交抛物线于 ,
, 两点,求证:
两点,求证:
(1)
 的斜率为
的斜率为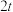 ;
;(2)
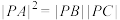 .
.
您最近一年使用:0次
3 . 已知点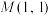 在抛物线
在抛物线 上.过点
上.过点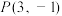 的直线l与抛物线C交于A,B两点(异于点M).
的直线l与抛物线C交于A,B两点(异于点M).
(1)若 的倾斜角为
的倾斜角为 ,求弦长
,求弦长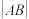 ;
;
(2)试探究直线AM与BM的斜率之积是否为定值:若为定值,求出该定值,若不是,说明理由.
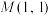 在抛物线
在抛物线 上.过点
上.过点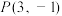 的直线l与抛物线C交于A,B两点(异于点M).
的直线l与抛物线C交于A,B两点(异于点M).(1)若
 的倾斜角为
的倾斜角为 ,求弦长
,求弦长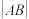 ;
;(2)试探究直线AM与BM的斜率之积是否为定值:若为定值,求出该定值,若不是,说明理由.
您最近一年使用:0次
4 . 抛物线C: 的焦点为F,过x轴上一点(其点在F右侧)的直线l交C于A,B两点,且C在A,B两点处的切线交于点P.
的焦点为F,过x轴上一点(其点在F右侧)的直线l交C于A,B两点,且C在A,B两点处的切线交于点P.
(1)若l: ,
, ,求C的方程;
,求C的方程;
(2)证明: .
.
 的焦点为F,过x轴上一点(其点在F右侧)的直线l交C于A,B两点,且C在A,B两点处的切线交于点P.
的焦点为F,过x轴上一点(其点在F右侧)的直线l交C于A,B两点,且C在A,B两点处的切线交于点P.(1)若l:
 ,
, ,求C的方程;
,求C的方程;(2)证明:
 .
.
您最近一年使用:0次
解题方法
5 . 已知抛物线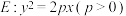 ,其焦点
,其焦点 与准线的距离为
与准线的距离为 ,若直线
,若直线 与
与 交于
交于 两点(直线
两点(直线 不垂直于
不垂直于 轴),且直线
轴),且直线 与
与 另一个交点为
另一个交点为 ,直线
,直线 与
与 另一个交点
另一个交点 .
.

(1)求抛物线 的方程;
的方程;
(2)若点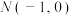 ,满足
,满足 恒成立,求证:直线
恒成立,求证:直线 过定点.
过定点.
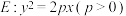 ,其焦点
,其焦点 与准线的距离为
与准线的距离为 ,若直线
,若直线 与
与 交于
交于 两点(直线
两点(直线 不垂直于
不垂直于 轴),且直线
轴),且直线 与
与 另一个交点为
另一个交点为 ,直线
,直线 与
与 另一个交点
另一个交点 .
.
(1)求抛物线
 的方程;
的方程;(2)若点
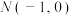 ,满足
,满足 恒成立,求证:直线
恒成立,求证:直线 过定点.
过定点.
您最近一年使用:0次
名校
解题方法
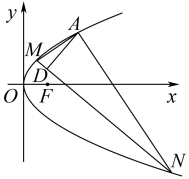
6 . 如图,已知抛物线 的焦点
的焦点 ,且经过点
,且经过点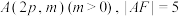 .
.
(1)求 和
和 的值;
的值;
(2)点 在
在 上,且
上,且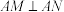 .过点
.过点 作
作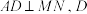 为垂足,问是否存在定点
为垂足,问是否存在定点 ,使得
,使得 为定值.若存在,求出点
为定值.若存在,求出点 坐标及
坐标及 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 的焦点
的焦点 ,且经过点
,且经过点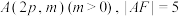 .
.
(1)求
 和
和 的值;
的值;(2)点
 在
在 上,且
上,且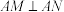 .过点
.过点 作
作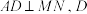 为垂足,问是否存在定点
为垂足,问是否存在定点 ,使得
,使得 为定值.若存在,求出点
为定值.若存在,求出点 坐标及
坐标及 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次
7 . 如图,已知抛物线 的焦点F,且经过点
的焦点F,且经过点 ,
,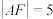 .
.

(1)求p和m的值;
(2)点M,N在C上,且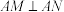 .过点A作
.过点A作 ,D为垂足,证明:存在定点Q,使得
,D为垂足,证明:存在定点Q,使得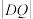 为定值.
为定值.
 的焦点F,且经过点
的焦点F,且经过点 ,
,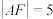 .
.
(1)求p和m的值;
(2)点M,N在C上,且
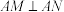 .过点A作
.过点A作 ,D为垂足,证明:存在定点Q,使得
,D为垂足,证明:存在定点Q,使得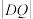 为定值.
为定值.
您最近一年使用:0次
2022-10-12更新
|
1231次组卷
|
5卷引用:浙江省十校联盟2022-2023学年高三上学期10月联考数学试题
22-23高二上·浙江·期末
名校
解题方法
8 . 设点 为抛物线
为抛物线 :
: (
( )的动点,
)的动点, 是抛物线的焦点,当
是抛物线的焦点,当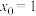 时,
时,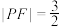 .
.
(1)求抛物线 的方程;
的方程;
(2)当 在第一象限且
在第一象限且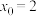 时,过
时,过 作斜率为
作斜率为 ,
, 的两条直线
的两条直线 ,
, ,分别交抛物线于点
,分别交抛物线于点 ,
, ,且
,且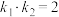 ,证明:直线
,证明:直线 恒过定点,并求该定点的坐标;
恒过定点,并求该定点的坐标;
(3)是否存在定圆 :
: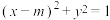 ,使得过曲线
,使得过曲线 上任意一点
上任意一点 作圆
作圆 的两条切线,与曲线
的两条切线,与曲线 交于另外两点
交于另外两点 ,
, 时,总有直线
时,总有直线 也与圆
也与圆 相切?若存在,求出
相切?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
 为抛物线
为抛物线 :
: (
( )的动点,
)的动点, 是抛物线的焦点,当
是抛物线的焦点,当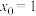 时,
时,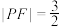 .
.(1)求抛物线
 的方程;
的方程;(2)当
 在第一象限且
在第一象限且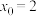 时,过
时,过 作斜率为
作斜率为 ,
, 的两条直线
的两条直线 ,
, ,分别交抛物线于点
,分别交抛物线于点 ,
, ,且
,且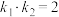 ,证明:直线
,证明:直线 恒过定点,并求该定点的坐标;
恒过定点,并求该定点的坐标;(3)是否存在定圆
 :
: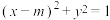 ,使得过曲线
,使得过曲线 上任意一点
上任意一点 作圆
作圆 的两条切线,与曲线
的两条切线,与曲线 交于另外两点
交于另外两点 ,
, 时,总有直线
时,总有直线 也与圆
也与圆 相切?若存在,求出
相切?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次
2022-09-29更新
|
777次组卷
|
5卷引用:高中数学 高二上-8
(已下线)高中数学 高二上-8江西省南昌市第二中学2022-2023学年高二上学期第二次月考数学试题河南省南阳市第五中学校2022-2023学年高二上学期第二次月考数学试题江西省上高二中2022-2023学年高二下学期2月月考数学试题(已下线)重难点突破14 阿基米德三角形(七大题型)
2021高三·全国·专题练习
9 . 如图,已知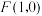 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作
作 的垂线,垂足为点
的垂线,垂足为点 ,且
,且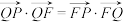 .
.

(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 的直线交轨迹
的直线交轨迹 于
于 两点,交直线
两点,交直线 于点
于点 .
.
(i)已知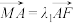 ,
,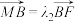 ,求
,求 的值;
的值;
(ii)求 的最小值.
的最小值.
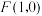 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点 作
作 的垂线,垂足为点
的垂线,垂足为点 ,且
,且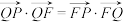 .
.
(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过点
 的直线交轨迹
的直线交轨迹 于
于 两点,交直线
两点,交直线 于点
于点 .
.(i)已知
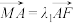 ,
,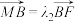 ,求
,求 的值;
的值;(ii)求
 的最小值.
的最小值.
您最近一年使用:0次
2022-10-28更新
|
1024次组卷
|
9卷引用:专题13 解析几何中的范围、最值和探索性问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》
(已下线)专题13 解析几何中的范围、最值和探索性问题(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题22 圆锥曲线中的定点、定值、定直线问题 微点2 圆锥曲线中的定值问题黑龙江省东风中学2021-2022学年高二下学期期中数学试题(已下线)第04讲 圆锥曲线综合(练)重庆市第十八中学2022-2023学年高二上学期线上素质测评数学试题江西省上饶市民校考试联盟2022-2023学年高二上学期12月联考数学试题(已下线)专题04 圆锥曲线定值问题-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)河北省曲阳县第一高级中学2021-2022学年高二上学期12月月考数学试题2007年普通高等学校招生考试数学(文)试题(福建卷)
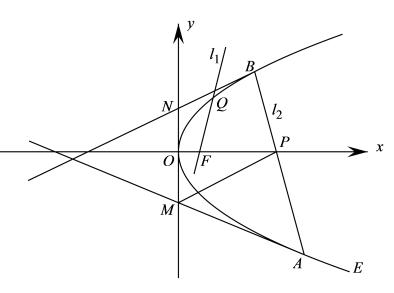
10 . 如图,过抛物线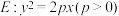 的焦点F的直线
的焦点F的直线 交抛物线于第一象限的点
交抛物线于第一象限的点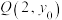 ,且
,且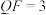 ,过点
,过点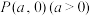 (不同于焦点F)的直线
(不同于焦点F)的直线 与抛物线E交于A,B,过A作抛物线的切线交y轴于M,过B作
与抛物线E交于A,B,过A作抛物线的切线交y轴于M,过B作 的平行线交y轴于N.
的平行线交y轴于N.
(1)求抛物线方程及直线 的斜率;
的斜率;
(2)记 为
为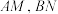 与y轴围成三角形的面积,是否存在实数
与y轴围成三角形的面积,是否存在实数 使
使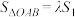 ,若存在,求出实数
,若存在,求出实数 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
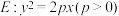 的焦点F的直线
的焦点F的直线 交抛物线于第一象限的点
交抛物线于第一象限的点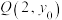 ,且
,且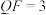 ,过点
,过点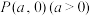 (不同于焦点F)的直线
(不同于焦点F)的直线 与抛物线E交于A,B,过A作抛物线的切线交y轴于M,过B作
与抛物线E交于A,B,过A作抛物线的切线交y轴于M,过B作 的平行线交y轴于N.
的平行线交y轴于N.
(1)求抛物线方程及直线
 的斜率;
的斜率;(2)记
 为
为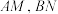 与y轴围成三角形的面积,是否存在实数
与y轴围成三角形的面积,是否存在实数 使
使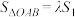 ,若存在,求出实数
,若存在,求出实数 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
您最近一年使用:0次



