解题方法
1 . 已知椭圆 的离心率为
的离心率为 ,
, 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 是椭圆上一点,且
是椭圆上一点,且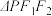 的周长是6,
的周长是6,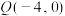 .
.
(1)求椭圆 的方程;
的方程;
(2)设直线 经过椭圆的左焦点
经过椭圆的左焦点 且与椭圆
且与椭圆 交于不同的两点
交于不同的两点 ,求证:直线
,求证:直线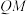 与直线
与直线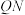 的斜率的和为定值.
的斜率的和为定值.
 的离心率为
的离心率为 ,
, 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 是椭圆上一点,且
是椭圆上一点,且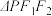 的周长是6,
的周长是6,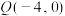 .
.(1)求椭圆
 的方程;
的方程;(2)设直线
 经过椭圆的左焦点
经过椭圆的左焦点 且与椭圆
且与椭圆 交于不同的两点
交于不同的两点 ,求证:直线
,求证:直线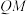 与直线
与直线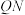 的斜率的和为定值.
的斜率的和为定值.
您最近一年使用:0次
名校
解题方法
2 . 在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: (
( )的离心率为
)的离心率为 ,焦距为
,焦距为 ,其上、下顶点分别为
,其上、下顶点分别为 、
、 ,直线
,直线 :
: 与
与 轴交于点
轴交于点 ,点
,点 是椭圆上的动点(异于
是椭圆上的动点(异于 、
、 ),直线
),直线 、
、 分别与直线
分别与直线 :
: 交于点
交于点 、
、 ,连接
,连接 ,与椭圆
,与椭圆 交于点
交于点
(1)求椭圆 的标准方程;
的标准方程;
(2)设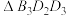 的面积为
的面积为 ,
,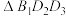 的面积为
的面积为 ,试判断
,试判断 是否为定值?并说明理由
是否为定值?并说明理由
 中,已知椭圆
中,已知椭圆 :
: (
( )的离心率为
)的离心率为 ,焦距为
,焦距为 ,其上、下顶点分别为
,其上、下顶点分别为 、
、 ,直线
,直线 :
: 与
与 轴交于点
轴交于点 ,点
,点 是椭圆上的动点(异于
是椭圆上的动点(异于 、
、 ),直线
),直线 、
、 分别与直线
分别与直线 :
: 交于点
交于点 、
、 ,连接
,连接 ,与椭圆
,与椭圆 交于点
交于点
(1)求椭圆
 的标准方程;
的标准方程;(2)设
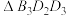 的面积为
的面积为 ,
,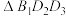 的面积为
的面积为 ,试判断
,试判断 是否为定值?并说明理由
是否为定值?并说明理由
您最近一年使用:0次
名校
解题方法
3 . 已知椭圆 的离心率为
的离心率为 ,以
,以 的长轴为直径的圆的方程为
的长轴为直径的圆的方程为 .
.
(1)求 的方程;
的方程;
(2)直线 与
与 轴平行,且与
轴平行,且与 交于
交于 ,
, 两点,
两点, ,
, 分别为
分别为 的左、右顶点.直线
的左、右顶点.直线 与
与 交于点
交于点 ,证明:点
,证明:点 与点
与点 的横坐标的乘积为定值.
的横坐标的乘积为定值.
 的离心率为
的离心率为 ,以
,以 的长轴为直径的圆的方程为
的长轴为直径的圆的方程为 .
.(1)求
 的方程;
的方程;(2)直线
 与
与 轴平行,且与
轴平行,且与 交于
交于 ,
, 两点,
两点, ,
, 分别为
分别为 的左、右顶点.直线
的左、右顶点.直线 与
与 交于点
交于点 ,证明:点
,证明:点 与点
与点 的横坐标的乘积为定值.
的横坐标的乘积为定值.
您最近一年使用:0次
2021-01-17更新
|
398次组卷
|
5卷引用:吉林省白城市第一中学2021届高三下学期质量检测数学(理)试题
4 . 已知椭圆 的离心率为
的离心率为 ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
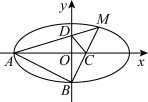
(1)求椭圆 的方程;
的方程;
(2)设点 为椭圆上位于第一象限内一动点,
为椭圆上位于第一象限内一动点, 分别为椭圆的左顶点和下顶点,直线
分别为椭圆的左顶点和下顶点,直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,求证:四边形
,求证:四边形 的面积为定值.
的面积为定值.
 的离心率为
的离心率为 ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆
 的方程;
的方程;(2)设点
 为椭圆上位于第一象限内一动点,
为椭圆上位于第一象限内一动点, 分别为椭圆的左顶点和下顶点,直线
分别为椭圆的左顶点和下顶点,直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,求证:四边形
,求证:四边形 的面积为定值.
的面积为定值.
您最近一年使用:0次
2021-08-07更新
|
1582次组卷
|
20卷引用:【全国百强校】吉林省实验中学2019届高三上学期第四次模拟考试数学(文)试题
【全国百强校】吉林省实验中学2019届高三上学期第四次模拟考试数学(文)试题【省级联考】福建省2019届高中毕业班数学学科备考关键问题指导系列数学(文科)适应性练习(二)【全国百强校】北京市清华大学附属中学2019届高三下学期第三次模拟考试数学(文)试题江西省上饶市横峰中学2020届高三下学期高考适应性考试数学(理)试题(已下线)专题05 平面解析几何——2020年高考真题和模拟题理科数学分项汇编安徽省宣城市郎溪县2020届高三下学期仿真模拟考试(最后一卷)文科数学试题(已下线)【南昌新东方】江西省南昌十九中2020-2021学年高三上学期10月第一次月考数学(理)试题广东省珠海市第二中学2021届高三上学期10月月考数学试题广东省普宁市七校联合体2021届高三上学期(11月)第二次联考数学试题(已下线)模块检测卷三(B卷 滚动提升检查)-2021年高考数学一轮复习单元滚动双测卷(新高考地区专用)江苏省南京市玄武高级中学、人民中学2021-2022学年高三上学期期初考前模拟数学试题(已下线)第45讲 解析几何的三角形、四边形面积问题及面积比问题-2022年新高考数学二轮专题突破精练(已下线)必刷卷03 (文)-2022年高考数学考前信息必刷卷(全国乙卷)(已下线)专题39 圆锥曲线中的定点、定值问题-1辽宁省丹东市凤城市第一中学2018-2019学年高二(下)4月月考数学(文科)试题江西省宜春市宜丰中学2019-2020学年高二下学期开学考试数学(理科)试题江西省靖安中学2019-2020学年高二下学期第一次月考数学(理)试题河北省邯郸市大名中学2019-2020学年高二(清北班)下学期第五次半月考(6月9日)数学试题江西省新余市2020-2021学年高二下学期期末数学(文)试题人教B版(2019) 选修第一册 过关检测 第二章 专题6 直线与圆锥曲线的综合问题
名校
解题方法
5 . 已知椭圆 的离心率为
的离心率为 ,
, 、
、 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 是椭圆上一点,且
是椭圆上一点,且 的周长是6.
的周长是6.
(1)求椭圆 的方程;
的方程;
(2)设直线 经过椭圆的右焦点
经过椭圆的右焦点 且与
且与 交于不同的两点
交于不同的两点 ,
, ,试问:在
,试问:在 轴上是否存在点
轴上是否存在点 ,使得直线
,使得直线 与直线
与直线 的斜率的和为定值?若存在,请求出点
的斜率的和为定值?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的离心率为
的离心率为 ,
, 、
、 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 是椭圆上一点,且
是椭圆上一点,且 的周长是6.
的周长是6.(1)求椭圆
 的方程;
的方程;(2)设直线
 经过椭圆的右焦点
经过椭圆的右焦点 且与
且与 交于不同的两点
交于不同的两点 ,
, ,试问:在
,试问:在 轴上是否存在点
轴上是否存在点 ,使得直线
,使得直线 与直线
与直线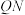 的斜率的和为定值?若存在,请求出点
的斜率的和为定值?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
2020-10-08更新
|
1343次组卷
|
9卷引用:吉林省长春外国语学校2021-2022学年高三下学期期初考试数学(文)试题
名校
解题方法
6 . 已知椭圆 :
: (
( )的左、右顶点分别为
)的左、右顶点分别为 、
、 ,焦距为2,点
,焦距为2,点 为椭圆上异于
为椭圆上异于 、
、 的点,且直线
的点,且直线 和
和 的斜率之积为
的斜率之积为 .
.
(1)求 的方程;
的方程;
(2)设直线 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 作
作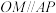 交椭圆于点
交椭圆于点 ,试证明
,试证明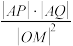 为定值,并求出该定值.
为定值,并求出该定值.
 :
: (
( )的左、右顶点分别为
)的左、右顶点分别为 、
、 ,焦距为2,点
,焦距为2,点 为椭圆上异于
为椭圆上异于 、
、 的点,且直线
的点,且直线 和
和 的斜率之积为
的斜率之积为 .
.(1)求
 的方程;
的方程;(2)设直线
 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 作
作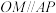 交椭圆于点
交椭圆于点 ,试证明
,试证明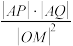 为定值,并求出该定值.
为定值,并求出该定值.
您最近一年使用:0次
2020-04-12更新
|
724次组卷
|
4卷引用:2020届吉林省长春市高三质量监测(二)文科数学试题
名校
解题方法
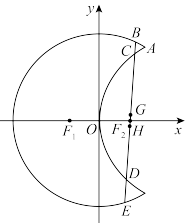
7 . 如图,曲线 是以原点
是以原点 为中心、
为中心、 ,
, 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 为顶点、
为顶点、 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线 和
和 的交点且
的交点且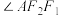 为钝角,若
为钝角,若 ,
,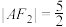 .
.
(1)求曲线 和
和 的方程;
的方程;
(2)过 作一条与
作一条与 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 ,
, 依次交于
依次交于 ,
, ,
, ,
, 四点,若
四点,若 为
为 中点,
中点, 为
为 中点,问
中点,问 是否为定值?若是,求出定值;若不是,说明理由.
是否为定值?若是,求出定值;若不是,说明理由.
 是以原点
是以原点 为中心、
为中心、 ,
, 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 为顶点、
为顶点、 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, 是曲线
是曲线 和
和 的交点且
的交点且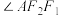 为钝角,若
为钝角,若 ,
,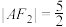 .
.
(1)求曲线
 和
和 的方程;
的方程;(2)过
 作一条与
作一条与 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线 ,
, 依次交于
依次交于 ,
, ,
, ,
, 四点,若
四点,若 为
为 中点,
中点, 为
为 中点,问
中点,问 是否为定值?若是,求出定值;若不是,说明理由.
是否为定值?若是,求出定值;若不是,说明理由.
您最近一年使用:0次
2020-06-27更新
|
509次组卷
|
6卷引用:吉林省长春市普通高中2022届高三质量监测(五)数学(文)试题
名校
解题方法
8 . 已知椭圆 的离心率为
的离心率为 ,且上顶点
,且上顶点 到直线
到直线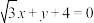 距离为3.
距离为3.
(1)求椭圆 的方程;
的方程;
(2)设直线 过点
过点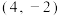 且与椭圆
且与椭圆 相交于
相交于 两点,
两点, 不经过点
不经过点 .证明:直线
.证明:直线 的斜率与直线
的斜率与直线 的斜率之和为定值.
的斜率之和为定值.
 的离心率为
的离心率为 ,且上顶点
,且上顶点 到直线
到直线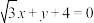 距离为3.
距离为3.(1)求椭圆
 的方程;
的方程;(2)设直线
 过点
过点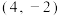 且与椭圆
且与椭圆 相交于
相交于 两点,
两点, 不经过点
不经过点 .证明:直线
.证明:直线 的斜率与直线
的斜率与直线 的斜率之和为定值.
的斜率之和为定值.
您最近一年使用:0次
2020-12-03更新
|
1025次组卷
|
6卷引用:吉林省实验中学2018届高三上学期第五次月考(一模)数学(文)试题
9 . 已知 的两个顶点
的两个顶点 的坐标分别为
的坐标分别为 ,
, ,且
,且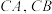 所在直线的斜率之积等于
所在直线的斜率之积等于 ,记顶点
,记顶点 的轨迹为
的轨迹为 .
.
(Ⅰ)求顶点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)若直线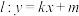 与曲线
与曲线 交于
交于 两点,点
两点,点 在曲线
在曲线 上,且
上,且 为
为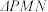 的重心(
的重心( 为坐标原点),求证:
为坐标原点),求证: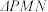 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
 的两个顶点
的两个顶点 的坐标分别为
的坐标分别为 ,
, ,且
,且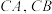 所在直线的斜率之积等于
所在直线的斜率之积等于 ,记顶点
,记顶点 的轨迹为
的轨迹为 .
.(Ⅰ)求顶点
 的轨迹
的轨迹 的方程;
的方程;(Ⅱ)若直线
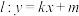 与曲线
与曲线 交于
交于 两点,点
两点,点 在曲线
在曲线 上,且
上,且 为
为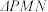 的重心(
的重心( 为坐标原点),求证:
为坐标原点),求证: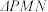 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
您最近一年使用:0次
2020-02-20更新
|
459次组卷
|
4卷引用:2020届吉林省长春市东北师大附中高三年级上学期第三次摸底数学(理)试题
2020届吉林省长春市东北师大附中高三年级上学期第三次摸底数学(理)试题四川省泸州市泸县第五中学2019-2020学年高三下学期第二次月考数学(理)试题四川省泸州市泸县第五中学2019-2020学年高三下学期第二次月考数学(文)试题(已下线)【新东方】【2021.5.25】【NB】【高二上】【高中数学】【NB00087】
10 . 已知椭圆 的离心率
的离心率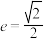 ,且椭圆过点
,且椭圆过点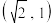
(1)求椭圆 的标准方程;
的标准方程;
(2)设直线 与
与 交于
交于 、
、 两点,点
两点,点 在椭圆
在椭圆 上,
上, 是坐标原点,若
是坐标原点,若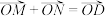 ,判定四边形
,判定四边形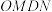 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
 的离心率
的离心率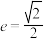 ,且椭圆过点
,且椭圆过点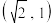
(1)求椭圆
 的标准方程;
的标准方程;(2)设直线
 与
与 交于
交于 、
、 两点,点
两点,点 在椭圆
在椭圆 上,
上, 是坐标原点,若
是坐标原点,若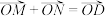 ,判定四边形
,判定四边形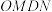 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
您最近一年使用:0次
2020-02-18更新
|
4246次组卷
|
21卷引用:2019届吉林省普通高三第三次联合模拟数学(文)试题
2019届吉林省普通高三第三次联合模拟数学(文)试题【市级联考】湖南省郴州市2019届高三第三次质量检测数学(文)试题【市级联考】陕西省榆林市2019届高三第四次普通高等学校招生模拟考试文科数学试题2020届河南省南阳市高三上学期期末数学(理)试题2020届河南省信阳市高三第二次教学质量检测数学(理)试题2019届湖南省长沙市雅礼中学高三下学期5月月考数学(文)试题2019届陕西省榆林市高三第四次模拟考试数学(文)试题(已下线)提升套餐练05-【新题型】2020年新高考数学多选题与热点解答题组合练(已下线)冲刺卷05-决战2020年高考数学冲刺卷(山东专版)2020届河南省开封市第五中学高三第四次教学质量检测数学(理)试卷(已下线)专题31 圆锥曲线中的定点、定值、探索性问题-冲刺2020高考跳出题海之高三数学模拟试题精中选萃(已下线)专题06 解析几何中的定点、定值问题(第五篇)-备战2020年高考数学大题精做之解答题题型全覆盖2020届黑龙江省大庆实验中学高三第一次模拟数学(文)试题河南省信阳市2020届高三上学期第二次教学质量检测(期末)数学(文)试题湖南省邵阳市邵东县第一中学2020-2021学年高三上学期第二次月考数学试题苏教版(2019) 选修第一册 选填专练 第3章 微专题七 高考中圆锥曲线问题(3):证明与探索性问题河南省许平汝联盟2021-2022学年高三下学期4月模拟考试文科数学试题河南省鹤壁市浚县第一中学2021-2022学年高三下学期4月考试文科数学试题湖南省长沙市明德中学2019-2020学年高二上学期期中数学试题江西省信丰中学2021-2022学年高二下学期第一次月考数学(理)B层试题宁夏中卫市中宁县2022-2023学年高二上学期质量测查(期末)数学(理)试题



