【课后练 】 2.4.3 向量与夹角 课后作业-湘教版(2019)选择性必修第二册 第2章 空间向量与立体几何
全国
高二
课后作业
2024-08-11
44次
整体难度:
容易
考查范围:
空间向量与立体几何
一、单选题 添加题型下试题
 的一个法向量为
的一个法向量为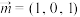 ,平面
,平面 的一个法向量是
的一个法向量是 ,则平面
,则平面 与
与 所成的角等于( )
所成的角等于( )A. | B. | C. | D.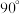 |
【知识点】 面面角的向量求法
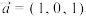 ,
,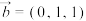 ,则斜线l与平面α所成的角为( )
,则斜线l与平面α所成的角为( )| A.30° | B.45° | C.60° | D.90° |
【知识点】 线面角的向量求法
 ,
, ,
,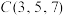 ,
,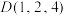 ,则直线
,则直线 和直线
和直线 所成角的余弦值为( )
所成角的余弦值为( )A.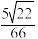 | B. | C.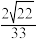 | D.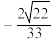 |
【知识点】 求异面直线所成的角 异面直线夹角的向量求法
 所在平面外一点
所在平面外一点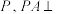 平面
平面 .若
.若 ,则平面
,则平面 与平面
与平面 所成的角的度数为( )
所成的角的度数为( )| A.30° | B.45° | C.60° | D.90° |
【知识点】 求二面角
 的底面ABCD是等腰梯形,
的底面ABCD是等腰梯形, ,且
,且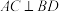 ,AC与BD交于O,
,AC与BD交于O, 底面ABCD,
底面ABCD,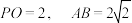 ,E,F分别是AB,AP的中点.则二面角
,E,F分别是AB,AP的中点.则二面角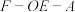 的余弦值为( )
的余弦值为( )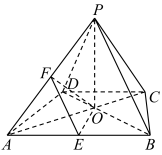
A. | B. | C.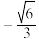 | D. |
【知识点】 面面角的向量求法
二、多选题 添加题型下试题
 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形,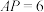 ,
,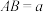 .若在直线
.若在直线 上存在两个不同点
上存在两个不同点 ,使得直线
,使得直线 与平面
与平面 所成角都为
所成角都为 .则实数
.则实数 的值为( )
的值为( )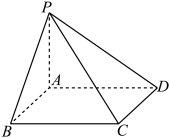
A. | B. | C. | D. |
【知识点】 由线面角的大小求长度
三、填空题 添加题型下试题
【知识点】 线面角的向量求法
四、解答题 添加题型下试题
 中,平面
中,平面 平面
平面 ,底面
,底面 为梯形,
为梯形,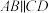 ,
, ,且
,且 ,
,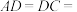
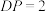 ,
,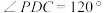 .求______所成角的余弦值.
.求______所成角的余弦值.从①平面
 与平面
与平面 ;②平面
;②平面 与平面
与平面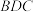 ;③平面
;③平面 与平面
与平面 这三个条件中任选一个,补充在题目中并作答.
这三个条件中任选一个,补充在题目中并作答.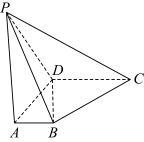
【知识点】 面面角的向量求法
五、单选题 添加题型下试题
 的对角线
的对角线 (不含端点)上.设
(不含端点)上.设 ,若
,若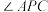 为钝角,则实数
为钝角,则实数 的取值范围为( )
的取值范围为( )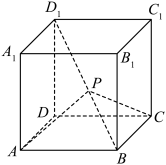
A. | B.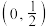 | C. | D.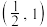 |
【知识点】 已知线线角求其他量
 ,
, 是直角梯形
是直角梯形 两腰的中点,
两腰的中点, 于
于 ,现将
,现将 沿
沿 折起,使平面
折起,使平面 与平面
与平面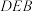 所成的角为
所成的角为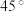 ,此时点
,此时点 在平面
在平面 内的射影恰为点
内的射影恰为点 ,则
,则 ,
, 的连线与
的连线与 所成的角的大小为( )
所成的角的大小为( )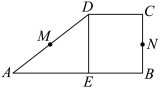
A.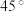 | B. | C. | D.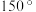 |
【知识点】 求异面直线所成的角 异面直线夹角的向量求法
六、填空题 添加题型下试题
 中,
中, 平面
平面 ,
, ,
, ,
,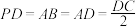 ,
, 为
为 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为
【知识点】 线面角的向量求法
 中,顶点
中,顶点 在空间直角坐标系的原点处,顶点
在空间直角坐标系的原点处,顶点 ,
, ,
, 分别在
分别在 ,
, ,
, 轴上,
轴上, 是线段
是线段 的中点,且
的中点,且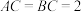 ,当
,当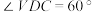 时,异面直线
时,异面直线 与
与 所成角的余弦值为
所成角的余弦值为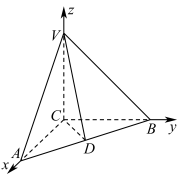
【知识点】 异面直线夹角的向量求法
七、解答题 添加题型下试题
 ,如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长均为1,点M在棱DG上.
,如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长均为1,点M在棱DG上.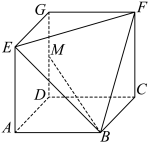
 ;
;(2)是否存在点M,使得直线MB与平面BEF所成的角为
 ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
【知识点】 空间位置关系的向量证明 已知线面角求其他量
试卷分析
导出试卷题型(共 16题)
试卷难度
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、单选题 | |||
| 1 | 0.94 | 面面角的向量求法 | |
| 2 | 0.85 | 线面角的向量求法 | |
| 3 | 0.94 | 求异面直线所成的角 异面直线夹角的向量求法 | |
| 4 | 0.65 | 求二面角 | |
| 5 | 0.65 | 面面角的向量求法 | |
| 11 | 0.65 | 已知线线角求其他量 | |
| 12 | 0.94 | 求异面直线所成的角 异面直线夹角的向量求法 | |
| 二、多选题 | |||
| 6 | 0.65 | 由线面角的大小求长度 | |
| 三、填空题 | |||
| 7 | 0.85 | 线面角的向量求法 | 单空题 |
| 8 | 0.65 | 面面角的向量求法 已知面面角求其他量 | 单空题 |
| 13 | 0.65 | 线面角的向量求法 | 单空题 |
| 14 | 0.85 | 异面直线夹角的向量求法 | 单空题 |
| 15 | 0.65 | 求异面直线所成的角 二面角的概念及辨析 | 单空题 |
| 四、解答题 | |||
| 9 | 0.65 | 异面直线夹角的向量求法 | 问答题 |
| 10 | 0.65 | 面面角的向量求法 | 问答题 |
| 16 | 0.65 | 空间位置关系的向量证明 已知线面角求其他量 | 证明题 |

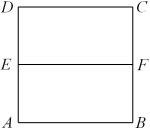
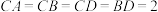 ,
,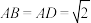 ,求异面直线
,求异面直线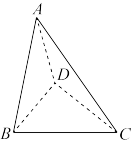
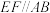 ,若沿EF将正方形折成一个二面角后,
,若沿EF将正方形折成一个二面角后,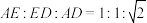 ,则AF与CE所成的角的余弦值为
,则AF与CE所成的角的余弦值为