17-18高一上·上海浦东新·期中
名校
1 . 设集合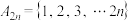
 ,如果对于
,如果对于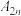 的每一个含有
的每一个含有
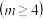 个元素的子集
个元素的子集 ,
, 中必有
中必有 个元素的和等于
个元素的和等于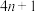 ,称正整数
,称正整数 为集合
为集合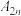 的一个“相关数”
的一个“相关数”
(1)当 时,判断
时,判断 和
和 是否为集合
是否为集合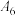 的“相关数”,说明理由;
的“相关数”,说明理由;
(2)若 为集合
为集合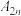 的“相关数”,证明:
的“相关数”,证明: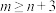 .
.
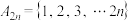
 ,如果对于
,如果对于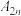 的每一个含有
的每一个含有
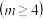 个元素的子集
个元素的子集 ,
, 中必有
中必有 个元素的和等于
个元素的和等于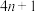 ,称正整数
,称正整数 为集合
为集合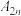 的一个“相关数”
的一个“相关数”(1)当
 时,判断
时,判断 和
和 是否为集合
是否为集合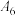 的“相关数”,说明理由;
的“相关数”,说明理由;(2)若
 为集合
为集合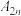 的“相关数”,证明:
的“相关数”,证明: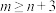 .
.
您最近一年使用:0次
2 . 定义区间 ,
,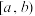 ,
, ,
, 的长度均为
的长度均为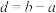 ,多个区间并集的长度为各区间长度之和,例如
,多个区间并集的长度为各区间长度之和,例如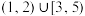 的长度
的长度 ,设
,设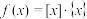 ,
,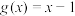 ,其中
,其中 表示不超过
表示不超过 的最大整数,
的最大整数,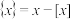 .若用
.若用 表示不等式
表示不等式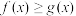 解集区间的长度,则当
解集区间的长度,则当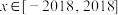 时,
时,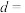
________ ;
 ,
,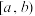 ,
, ,
, 的长度均为
的长度均为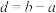 ,多个区间并集的长度为各区间长度之和,例如
,多个区间并集的长度为各区间长度之和,例如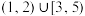 的长度
的长度 ,设
,设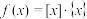 ,
, ,其中
,其中 表示不超过
表示不超过 的最大整数,
的最大整数,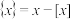 .若用
.若用 表示不等式
表示不等式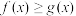 解集区间的长度,则当
解集区间的长度,则当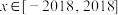 时,
时,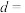
您最近一年使用:0次
2019-12-10更新
|
564次组卷
|
2卷引用:上海市七宝中学2018-2019学年高一上学期第一次月考数学试题
18-19高一上·上海浦东新·期中
名校
3 . 已知集合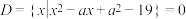 ,
,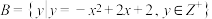 ,集合
,集合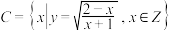 ,且集合
,且集合 满足
满足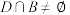 ,
, .
.
(1)求实数 的值;
的值;
(2)对集合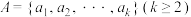 ,其中
,其中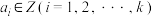 ,定义由
,定义由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: ,
,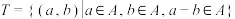 ,其中
,其中 是有序数对,集合
是有序数对,集合 和
和 中的元素个数分别为
中的元素个数分别为 和
和 ,若对任意的
,若对任意的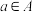 ,总有
,总有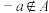 ,则称集合
,则称集合 具有性质
具有性质 .
.
①请检验集合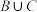 与
与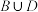 是否具有性质
是否具有性质 ,并对其中具有性质
,并对其中具有性质 的集合,写出相应的集合
的集合,写出相应的集合 和
和 ;
;
②试判断 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
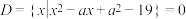 ,
,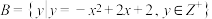 ,集合
,集合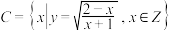 ,且集合
,且集合 满足
满足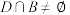 ,
, .
.(1)求实数
 的值;
的值;(2)对集合
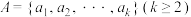 ,其中
,其中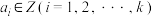 ,定义由
,定义由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: ,
,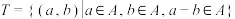 ,其中
,其中 是有序数对,集合
是有序数对,集合 和
和 中的元素个数分别为
中的元素个数分别为 和
和 ,若对任意的
,若对任意的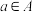 ,总有
,总有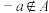 ,则称集合
,则称集合 具有性质
具有性质 .
.①请检验集合
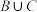 与
与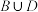 是否具有性质
是否具有性质 ,并对其中具有性质
,并对其中具有性质 的集合,写出相应的集合
的集合,写出相应的集合 和
和 ;
;②试判断
 和
和 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
名校
4 . 将含有 个正整数的集合
个正整数的集合 分成元素个数相等且两两没有公共元素的三个集合
分成元素个数相等且两两没有公共元素的三个集合 、
、 、
、 ,其中
,其中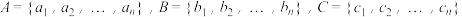 ,若
,若 、
、 、
、 中的元素满足条件:
中的元素满足条件: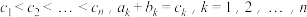 ,则称
,则称 为“完并集合”.
为“完并集合”.
(1)若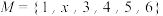 为“完并集合”,求
为“完并集合”,求 的值;
的值;
(2)对于“完并集合”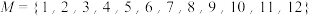 ,在所有符合条件的集合
,在所有符合条件的集合 中,求元素乘积最小的集合
中,求元素乘积最小的集合 .
.
 个正整数的集合
个正整数的集合 分成元素个数相等且两两没有公共元素的三个集合
分成元素个数相等且两两没有公共元素的三个集合 、
、 、
、 ,其中
,其中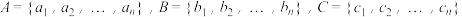 ,若
,若 、
、 、
、 中的元素满足条件:
中的元素满足条件: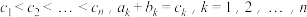 ,则称
,则称 为“完并集合”.
为“完并集合”.(1)若
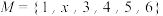 为“完并集合”,求
为“完并集合”,求 的值;
的值;(2)对于“完并集合”
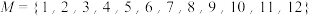 ,在所有符合条件的集合
,在所有符合条件的集合 中,求元素乘积最小的集合
中,求元素乘积最小的集合 .
.
您最近一年使用:0次
5 . 已知由自然数组成的 元集合
元集合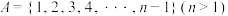 ,非空集合
,非空集合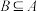 ,且对任意的
,且对任意的 ,都有
,都有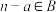 .
.
(1)当 时,求所有满足条件的集合
时,求所有满足条件的集合 ;
;
(2)当 时,求所有满足条件的集合
时,求所有满足条件的集合 的元素总和;
的元素总和;
(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合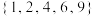 的交替和是
的交替和是 ,集合
,集合 的交替和为
的交替和为 .当
.当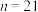 时,求所有满足条件的集合
时,求所有满足条件的集合 的“交替和”的总和.
的“交替和”的总和.
 元集合
元集合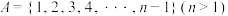 ,非空集合
,非空集合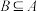 ,且对任意的
,且对任意的 ,都有
,都有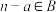 .
.(1)当
 时,求所有满足条件的集合
时,求所有满足条件的集合 ;
;(2)当
 时,求所有满足条件的集合
时,求所有满足条件的集合 的元素总和;
的元素总和;(3)定义一个集合的“交替和”如下:按照递减的次序重新排列该集合的元素,然后从最大数开始交替地减、加后继的数.例如集合
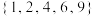 的交替和是
的交替和是 ,集合
,集合 的交替和为
的交替和为 .当
.当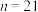 时,求所有满足条件的集合
时,求所有满足条件的集合 的“交替和”的总和.
的“交替和”的总和.
您最近一年使用:0次
名校
6 . 对于集合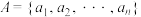 ,
,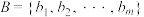 ,
,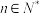 ,
, ,定义
,定义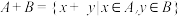 .集合
.集合 中的元素个数记为
中的元素个数记为 .规定:若集合
.规定:若集合 满足
满足 ,则称集合具
,则称集合具 有性质
有性质 .
.
(1)已知集合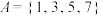 ,
, ,写出
,写出 ,
, 的值;
的值;
(2)已知集合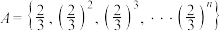 ,其中
,其中 ,证明:
,证明: 有性质
有性质 ;
;
(3)已知集合 ,
, 有性质
有性质 ,且
,且 求
求 的最小值.
的最小值.
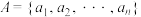 ,
,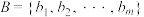 ,
,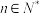 ,
, ,定义
,定义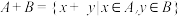 .集合
.集合 中的元素个数记为
中的元素个数记为 .规定:若集合
.规定:若集合 满足
满足 ,则称集合具
,则称集合具 有性质
有性质 .
.(1)已知集合
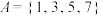 ,
, ,写出
,写出 ,
, 的值;
的值;(2)已知集合
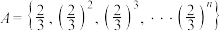 ,其中
,其中 ,证明:
,证明: 有性质
有性质 ;
;(3)已知集合
 ,
, 有性质
有性质 ,且
,且 求
求 的最小值.
的最小值.
您最近一年使用:0次
名校
7 . 已知 是满足下列条件的集合:①
是满足下列条件的集合:① ,
,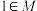 ;②若
;②若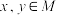 ,则
,则 ;③若
;③若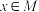 且
且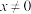 ,则
,则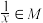 .
.
(1)判断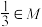 是否正确,说明理由;
是否正确,说明理由;
(2)证明:“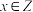 ”是“
”是“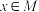 ”的充分条件;
”的充分条件;
(3)证明:若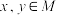 ,则
,则 .
.
 是满足下列条件的集合:①
是满足下列条件的集合:① ,
,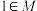 ;②若
;②若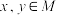 ,则
,则 ;③若
;③若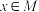 且
且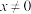 ,则
,则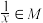 .
.(1)判断
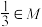 是否正确,说明理由;
是否正确,说明理由;(2)证明:“
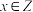 ”是“
”是“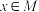 ”的充分条件;
”的充分条件;(3)证明:若
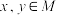 ,则
,则 .
.
您最近一年使用:0次
8 . 设集合 、
、 均为实数集
均为实数集 的子集,记:
的子集,记: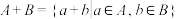 ;
;
(1)已知 ,
, ,试用列举法表示
,试用列举法表示 ;
;
(2)设 ,当
,当 ,且
,且 时,曲线
时,曲线 的焦距为
的焦距为 ,如果
,如果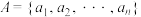 ,
,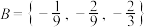 ,设
,设 中的所有元素之和为
中的所有元素之和为 ,对于满足
,对于满足 ,且
,且 的任意正整数
的任意正整数 、
、 、
、 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)若整数集合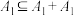 ,则称
,则称 为“自生集”,若任意一个正整数均为整数集合
为“自生集”,若任意一个正整数均为整数集合 的某个非空有限子集中所有元素的和,则称
的某个非空有限子集中所有元素的和,则称 为“
为“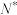 的基底集”,问:是否存在一个整数集合既是自生集又是
的基底集”,问:是否存在一个整数集合既是自生集又是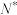 的基底集?请说明理由.
的基底集?请说明理由.
 、
、 均为实数集
均为实数集 的子集,记:
的子集,记: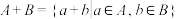 ;
;(1)已知
 ,
, ,试用列举法表示
,试用列举法表示 ;
;(2)设
 ,当
,当 ,且
,且 时,曲线
时,曲线 的焦距为
的焦距为 ,如果
,如果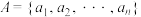 ,
,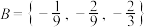 ,设
,设 中的所有元素之和为
中的所有元素之和为 ,对于满足
,对于满足 ,且
,且 的任意正整数
的任意正整数 、
、 、
、 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;(3)若整数集合
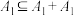 ,则称
,则称 为“自生集”,若任意一个正整数均为整数集合
为“自生集”,若任意一个正整数均为整数集合 的某个非空有限子集中所有元素的和,则称
的某个非空有限子集中所有元素的和,则称 为“
为“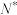 的基底集”,问:是否存在一个整数集合既是自生集又是
的基底集”,问:是否存在一个整数集合既是自生集又是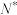 的基底集?请说明理由.
的基底集?请说明理由.
您最近一年使用:0次
9 . 设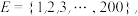 且
且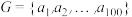 是E的真子集,且G具有下列两条性质:
是E的真子集,且G具有下列两条性质:
(1)对任何 恒有
恒有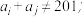
(2)
试证:G中的奇数的个数是4的倍数,且G中的所有数字的平方和为一个定数
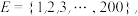 且
且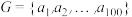 是E的真子集,且G具有下列两条性质:
是E的真子集,且G具有下列两条性质:(1)对任何
 恒有
恒有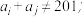
(2)

试证:G中的奇数的个数是4的倍数,且G中的所有数字的平方和为一个定数
您最近一年使用:0次
名校
10 . 设 是由
是由 个有序实数构成的一个数组,记作
个有序实数构成的一个数组,记作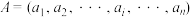 ,其中
,其中

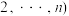 称为数组
称为数组 的“元”,
的“元”, 称为
称为 的下标,如果数组
的下标,如果数组 中的每个“元”都是来自数组
中的每个“元”都是来自数组
 中不同下标的“元”,则称
中不同下标的“元”,则称 为
为 的子数组,定义两个数组
的子数组,定义两个数组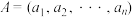 和
和
 的关系数为
的关系数为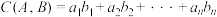 ;
;
(1)若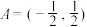 ,
,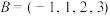 ,设
,设 是
是 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求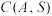
的最大值;
(2)若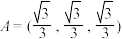 ,
,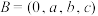 ,且
,且 ,
, 为
为 的含有三个“元”
的含有三个“元”
的子数组,求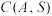 的最大值;
的最大值;
(3)若数组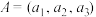 中的“元”满足
中的“元”满足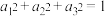 ,设数组
,设数组
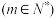 含有
含有
四个“元”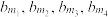 ,且
,且 ,求
,求 与
与 的所有含有三个“元”
的所有含有三个“元”
的子数组的关系数的最大值;
 是由
是由 个有序实数构成的一个数组,记作
个有序实数构成的一个数组,记作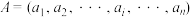 ,其中
,其中

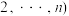 称为数组
称为数组 的“元”,
的“元”, 称为
称为 的下标,如果数组
的下标,如果数组 中的每个“元”都是来自数组
中的每个“元”都是来自数组 中不同下标的“元”,则称
中不同下标的“元”,则称 为
为 的子数组,定义两个数组
的子数组,定义两个数组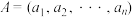 和
和
 的关系数为
的关系数为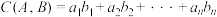 ;
;(1)若
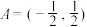 ,
,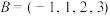 ,设
,设 是
是 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求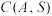
的最大值;
(2)若
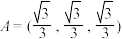 ,
,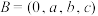 ,且
,且 ,
, 为
为 的含有三个“元”
的含有三个“元”的子数组,求
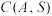 的最大值;
的最大值;(3)若数组
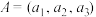 中的“元”满足
中的“元”满足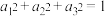 ,设数组
,设数组
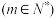 含有
含有四个“元”
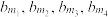 ,且
,且 ,求
,求 与
与 的所有含有三个“元”
的所有含有三个“元”的子数组的关系数的最大值;
您最近一年使用:0次



