1 . 某煤气站对外输送煤气时,用1至5号五个阀门控制,且必须遵守以下操作规则:
(i)若开启3号,则必须同时开启4号并且关闭2号;
(ii)若开启2号或4号,则关闭1号;
(iii)禁止同时关闭5号和1号.
现要开启3号,则同时开启的另两个阀门是__________ .
(i)若开启3号,则必须同时开启4号并且关闭2号;
(ii)若开启2号或4号,则关闭1号;
(iii)禁止同时关闭5号和1号.
现要开启3号,则同时开启的另两个阀门是
您最近一年使用:0次
2 . 2018年11月15日,我市召开全市创建全国文明城市动员大会,会议向全市人民发出动员令,吹响了集结号.为了了解哪些人更关注此活动,某机构随机抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为: ,
, ,
,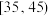 ,
,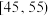 ,
, ,
,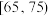 .把年龄落在
.把年龄落在 和
和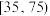 内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为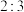 .
.
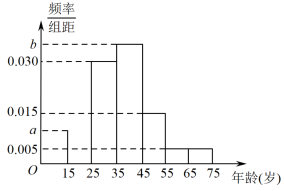
(1)求图中 的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值
的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值 ;
;
(2)若“青少年人”中有15人关注此活动,根据已知条件完成题中的 列联表,根据此统计结果,问能否有
列联表,根据此统计结果,问能否有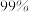 的把握认为“中老年人”比“青少年人”更加关注此活动?
的把握认为“中老年人”比“青少年人”更加关注此活动?
附参考公式: ,其中
,其中 .
.
 ,
, ,
,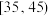 ,
,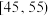 ,
, ,
,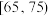 .把年龄落在
.把年龄落在 和
和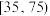 内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为 .
.
(1)求图中
 的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值
的值,若以每个小区间的中点值代替该区间的平均值,估计这100人年龄的平均值 ;
;(2)若“青少年人”中有15人关注此活动,根据已知条件完成题中的
 列联表,根据此统计结果,问能否有
列联表,根据此统计结果,问能否有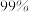 的把握认为“中老年人”比“青少年人”更加关注此活动?
的把握认为“中老年人”比“青少年人”更加关注此活动?| 关注 | 不关注 | 合计 | |
| 青少年人 | 15 | ||
| 中老年人 | |||
| 合计 | 50 | 50 | 100 |
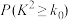 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
 ,其中
,其中 .
.
您最近一年使用:0次
2019-03-30更新
|
749次组卷
|
2卷引用:【校级联考】吉林省吉林市普通中学2019届高中毕业班第三次调研测试数学(文科)试题
名校
3 . 欧拉公式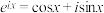 (
( 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,
为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,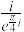 表示的复数位于复平面内
表示的复数位于复平面内
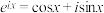 (
( 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,
为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,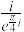 表示的复数位于复平面内
表示的复数位于复平面内| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
您最近一年使用:0次
2019-03-30更新
|
517次组卷
|
4卷引用:【校级联考】吉林省吉林市普通中学2019届高中毕业班第三次调研测试数学(文科)试题
2019·陕西·高考模拟
名校
4 . 一布袋中装有 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是
 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是A.若 ,则乙有必赢的策略 ,则乙有必赢的策略 | B.若 ,则甲有必赢的策略 ,则甲有必赢的策略 |
C.若 ,则甲有必赢的策略 ,则甲有必赢的策略 | D.若 ,则乙有必赢的策略 ,则乙有必赢的策略 |
您最近一年使用:0次
2019-03-20更新
|
840次组卷
|
8卷引用:吉林省舒兰市实验中学2019-2020学年高二下学期期中考试数学(文)试题
吉林省舒兰市实验中学2019-2020学年高二下学期期中考试数学(文)试题(已下线)【省级联考】陕西省2019届高三第二次教学质量检测数学(理)试题(已下线)【省级联考】陕西省2019届高三第二次教学质量检测数学(文)试题(已下线)2019年6月21日 《每日一题》文数-合情推理与演绎推理【全国百强校】河南省南阳市第一中学2018-2019学年高二下学期第四次月考数学(理)试题(已下线)狂刷55 推理与证明-学易试题君之小题狂刷2020年高考数学(理)(已下线)专题12.1 合情推理与演绎推理 (精练)-2021届高考数学(文)一轮复习学与练(已下线)专题12.1 合情推理与演绎推理 (精练)-2021年高考数学(理)一轮复习学与练
名校
5 . 学校艺术节对同一类的 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“ 作品获得一等奖”;乙说:“
作品获得一等奖”;乙说:“ 作品获得一等奖”;丙说:“
作品获得一等奖”;丙说:“ ,
, 两项作品未获得一等奖”;丁说:“是
两项作品未获得一等奖”;丁说:“是 或
或 作品获得一等奖”,若这四位同学中只有两位说的话是对的,则获得一等奖的作品是
作品获得一等奖”,若这四位同学中只有两位说的话是对的,则获得一等奖的作品是___ .
 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“ 作品获得一等奖”;乙说:“
作品获得一等奖”;乙说:“ 作品获得一等奖”;丙说:“
作品获得一等奖”;丙说:“ ,
, 两项作品未获得一等奖”;丁说:“是
两项作品未获得一等奖”;丁说:“是 或
或 作品获得一等奖”,若这四位同学中只有两位说的话是对的,则获得一等奖的作品是
作品获得一等奖”,若这四位同学中只有两位说的话是对的,则获得一等奖的作品是
您最近一年使用:0次
2019-07-07更新
|
576次组卷
|
57卷引用:内蒙古包头市第九中学2016-2017学年高二下学期期中考试数学(文)试题
内蒙古包头市第九中学2016-2017学年高二下学期期中考试数学(文)试题宁夏育才中学2016-2017学年高二下学期期中考试数学(理)试题辽宁省六校协作体2017-2018学年高三上学期期中考试数学(理)试题北京市东城区2018届高三上学期期中考试数学试题吉林省吉林市2018届高三第三次调研考试数学(文科)试题安徽师范大学附属中学2017-2018学年高二下学期期中考试数学(理)试题【全国市级联考】山西省运城市2017-2018学年高二下学期期中考试数学(文)试题【全国校级联考】辽宁省六校协作体2017-2018学年高二下学期期中考试数学(理)试题【市级联考】山东日照市2019届高三上学期期中考试(数学理)试题北京市北京外国语大学附属中学2018-2019学年高二年级第二学期期中测试数学(理)试题吉林省延边第二中学2020-2021学年高二下学期期中考试数学(理)试题四川省成都市简阳市阳安中学2022-2023学年高二下学期期中考试数学(文)试题2017届四川遂宁等四市高三一诊联考数学(理)试卷2017届陕西省咸阳市高三模拟考试(三)数学(文)试卷2017届陕西省咸阳市高三模拟考试(三)数学(理)试卷2017届宁夏银川市高三下学期第二次模拟考试数学(理)试卷江西省瑞昌市第二中学2016-2017学年高二下学期第二次段考数学(文)试题安徽省蚌埠市2017届高三第三次教学质量检查数学(文)试题河南省商丘市九校2016-2017学年高二下学期期末联考数学(文)试题安徽省亳州市第二中学2017届高三下学期教学质量检测数学(文)试题四川省内江市2016-2017学年高二下学期期末检测数学(理)试题四川省内江市2016-2017学年高二下学期期末检测数学(文)试题河南省周口市2016-2017学年高二下学期期末考试文数试题内蒙古太仆寺旗宝昌一中2016-2017学年高二下学期期末考试理科数学试卷重庆市第一中学2018届高三上学期第一次月考(9月)数学(理)试题河北省衡水市武邑中学2018届高三上学期第三次调研考试数学(理)试题2河北省衡水市武邑中学2018届高三上学期第三次调研考试数学(理)试题1湖南省株洲市醴陵第二中学、醴陵第四中学2018届高三上学期两校期中联考数学(文)试题四川省(大教育联盟)邻水实验学校2018届高三上学期第三次月考数学(文)试题福建省厦门外国语学校2018届高三下学期第一次(开学)考试数学(理)试题福建省厦门外国语学校2018届高三下学期第一次(开学)考试数学(文)试题宁夏吴忠市2018届高三下学期高考模拟联考数学(文)试题【全国市级联考】新疆维吾尔自治区乌鲁木齐地区2018届高三5月适应性训练数学(理)试题【全国市级联考】新疆乌鲁木齐地区2018届高三5月适应性训练数学文试题(已下线)2018年5月25日 押高考数学第15题——《每日一题》2018年高三理科数学四轮复习 (已下线)2018年5月25日 押高考数学第15题——《每日一题》2018年高三文科数学四轮复习 河南省兰考县第二高级中学2017-2018学年高二下学期期末高中抽测调研数学(文)试题【全国百强校】湖北省宜昌市第一中学2017-2018学年高二下学期期末考试数学(理)试题【全国县级联考】河北省邯郸市鸡泽、曲周、邱县、馆陶四县2017-2018学年高二下学期期末联考数学(理)试题【市级联考】四川省宜宾市第四中学2019届高三12月月考数学(文)试题四川省宜宾市第四中学2019届高三12月月考数学(理)试题【全国百强校】四川外语学院重庆第二外国语学校2017届高三下学期第二次检测数学(文)试题江西省宜丰中学2019届高三上学期第四次月考数学(文)试题甘肃省武威第十八中学2019届高三上学期期末考试数学(理)试题黑龙江省哈尔滨市第三中学2019届高三第一次模拟考试(内考)数学(理)试题黑龙江省哈尔滨市第三中学2019届高三第一次模拟考试(内考)数学(文)试题【全国百强校】北京师范大学附属实验中学2019届高三下学期第一次质量评估文科数学试题【全国百强校】河北省邢台市第一中学2018-2019学年高二下学期第一次月考数学(文)试题内蒙古通辽实验中学2018-2019学年高二下学期第一次月考数学(理)试题内蒙古集宁一中2018-2019学年高二6月月考数学(文)试题2019届湖南省长沙市第一中学高考模拟数学(理)试题黑龙江省鹤岗市第一中学2020-2021学年高三上学期第二次月考数学(文)试题(已下线)期末综合检测05-2020-2021学年高二数学下学期期末专项复习(苏教版选修2-2、2-3)河南省开封市五县部分校2021-2022学年高二下学期月考数学(文)试题河南省南阳市第一中学2021-2022学年高二下学期第四次月考文科数学试题宁夏回族自治区银川一中2023届高三上学期第一次月考数学(文)试题宁夏回族自治区银川一中2023届高三上学期第一次月考数学(理)试题
名校
6 . “中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 .
.
(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列及均值.
附: .
.
男性 | 女性 | 总计 | |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
 .
.(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列及均值.
附:
 .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次
2018-10-07更新
|
1207次组卷
|
5卷引用:【全国百强校】吉林省吉林市吉化第一高级中学2018-2019学年高二下学期期中考试数学试题
【全国百强校】吉林省吉林市吉化第一高级中学2018-2019学年高二下学期期中考试数学试题2018-2019学年高中数学选修2-3人教版练习:模块综合评价(二)【全国百强校】广东省佛山市第二中学2018-2019学年第二学期第三次月考高二级数学(理)试题(已下线)8.3 列联表与独立性检验 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)专题25 独立性检验(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)
9-10高二下·福建·期中
7 . 设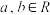 ,“
,“ ”是“复数
”是“复数 是纯虚数”的
是纯虚数”的
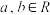 ,“
,“ ”是“复数
”是“复数 是纯虚数”的
是纯虚数”的| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2019-01-30更新
|
5592次组卷
|
52卷引用:2014-2015学年吉林省吉林市五十五中高二下学期期中考试文科数学卷
2014-2015学年吉林省吉林市五十五中高二下学期期中考试文科数学卷(已下线)福建师大附中2009-2010学年第二学期期中考试卷高二数学文科选修2-2(已下线)2013-2014学年河北省保定市高二下学期期中考试理科数学试卷【全国市级联考】四川省眉山一中2017-2018学年高二下学期期中考试数学(文)试卷山西省沁县中学2017-2018学年高二下学期期中考试数学(文)试题江西省赣州中学2019届高三上学期期中考试数学(理科)试题【全国百强校】湖北省沙市中学2018-2019学年高二下学期期中考试数学(文)试题【全国百强校】山西省平遥中学2018-2019学年高二下学期期中考试数学(文)试题江苏省无锡市天一中学2019-2020学年高二下学期期中数学试题北京市第五十中学 2019—2020 学年度高一第二学期期中考试数学试题北京市第二十二中学2023-2024学年高一下学期期中考试数学试卷2012年全国普通高等学校招生统一考试理科数学(北京卷)(已下线)2012-2013学年山东省临沂十八中高二下学期3月月考文科数学试卷(已下线)2012-2013学年广东省执信中学高二下学期期末考试理科数学试卷2015届四川省石室中学高三一诊模拟理科数学试卷2015届四川省石室中学高三一诊模拟文科数学试卷2015-2016学年江西省崇义中学高二下学期第一次月考文科数学试卷2017届湖南益阳市高三9月调研数学(文)试卷2016-2017学年北京市丰台区高三想上学期一模练习理数试卷【全国市级联考】河南省濮阳市2017-2018学年高二下学期升级考试数学(文)试题【全国校级联考】河北省卓越联盟2017-2018学年高二下学期第二次月考数学(文)试题河南省兰考县第二高级中学人教版高二数学选修2-2单元测试:第三章数系的扩充与复数的引入浙江省杭州市西湖高级中学2017-2018学年高二5月考数学试题四川省邻水实验学校2017-2018学年高二下学期第三次月考数学(理)试卷黑龙江省海林市朝鲜族中学人教版高中数学选修1-2同步练习:滚动习题第三章 数系的扩充与复数的引入[范围3.1~3.2]甘肃省武威第十八中学人教版高中数学选修2-2练习:第三章 数系的扩充与复数的引入【全国市级联考】湖北省黄冈市2018-2019学年高二下学期期末考试数学文试题河北省邯郸市大名一中2019-2020学年高三上学期第一次月考数学(理)试卷广东省惠州市2019-2020学年高二上学期期末数学试题人教A版(2019) 必修第二册 过关斩将 第七章 7.1 复数的概念 7.1.1 数系的扩充和复数的概念(已下线)专题02 常用逻辑用语-十年(2011-2020)高考真题数学分项天津市南开大学附中2020-2021学年高三上学期第一次月考数学试题(已下线)第五章 数系的扩充与复数的引入(基础过关)-2020-2021学年高二数学单元测试定心卷(北师大版选修2-2)(已下线)7.1.1 数系的扩充和复数的概念(练习)-2020-2021学年下学期高一数学同步精品课堂(新教材人教版必修第二册)宁夏青铜峡市高级中学2020-2021学年高二6月月考数学(理)试题江西省贵溪市实验中学高中部2020-2021学年高二下学期第三次月考数学(理)试题河南省商丘市安阳市部分高中2020-2021学年高二下学期第二次联考数学(理科)试题(已下线)考点45 数系的扩充与复数的引入-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点02 命题及其关系、充分与必要条件-备战2022年高考数学(理)一轮复习考点帮北师大版(2019) 必修第二册 金榜题名 进阶篇 三十五 复数的概念(已下线)专题12.1 复数的概念(重点练)-2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第二册)北京市中国农业大学附属中学2020-2021学年高一下学期期末数学试题北京市丰台区2019-2020学年高二上学期期末数学试题河南省豫北名校联盟2021-2022学年高二下学期联考二理科数学试题(已下线)7.1.1数系的扩充和复数的概念-【师说智慧课堂】课后作业(人教A版2019)(已下线)第01讲 复数的概念-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)浙江省温州市瑞安市第六中学2021-2022学年高一下学期3月月考数学试题北京名校2023届高三一轮总复习 第1章 集合与简易逻辑 1.3 常用逻辑用语3.1复数的概念湖南省衡阳市第八中学2023-2024学年高二创新班上学期第四阶段测试数学试题(已下线)考点6 复数的概念与几何意义 --2024届高考数学考点总动员【讲】(已下线)7.1.1数系的扩充和复数的概念【第一课】“上好三节课,做好三套题“高中数学素养晋级之路
名校
解题方法
8 .  市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办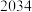 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了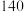 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有 位退休老人,其中
位退休老人,其中 位是教师,现从这
位是教师,现从这 位退休老人中随机抽取
位退休老人中随机抽取 人,求至多有
人,求至多有 位老师的概率.
位老师的概率.
附: ,其中
,其中 .
.
 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办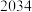 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了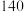 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过
 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;(ii)已知在被调查的支持申办足球世界杯的男性市民中有
 位退休老人,其中
位退休老人,其中 位是教师,现从这
位是教师,现从这 位退休老人中随机抽取
位退休老人中随机抽取 人,求至多有
人,求至多有 位老师的概率.
位老师的概率.附:
 ,其中
,其中 .
.
|
|
|
|
|
|
|
|
|
|
|
|
您最近一年使用:0次
2018-07-24更新
|
756次组卷
|
11卷引用:吉林省舒兰市实验中学2019-2020学年高二下学期期中考试数学(文)试题
吉林省舒兰市实验中学2019-2020学年高二下学期期中考试数学(文)试题【全国校级联考】福建省龙岩市武平一中、长汀一中、漳平一中等六校2017-2018学年高二下学期期中考试数学(文)试题河南省开封市五县联考2019-2020学年高二下学期期中考试数学(理)试题【全国校级联考】湖北省孝感市重点高中协作体2017-2018学年高二下学期期末联考数学(文)试题【全国市级联考】辽宁省辽阳市2017-2018学年高二下学期期末考试数学(文)试题【全国市级联考】辽宁省辽阳市2017-2018学年高二下学期期末考试数学(理)试题【全国百强校】吉林省长春市一五0中学2017-2018学年高二下学期期末考试理数试卷【全国百强校】吉林省长春市一五0中学2017-2018学年下学期高二数学(文)试题河南省名校联盟2019-2020学年高二3月联考数学(文)试题河南省林州市第一中学2019-2020学年高二4月月考数学(文)试题河南省平顶山市第一中学2019-2020学年高二下学期开学考试数学(文)试题
名校
9 . 学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式: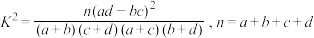 ,
,
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:
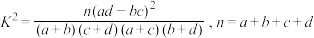 ,
,
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2019-04-03更新
|
574次组卷
|
4卷引用:2014-2015学年吉林省吉林市五十五中高二下学期期中考试文科数学卷
10 .
等差数列 的前
的前 项和为
项和为 ,
,
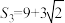
(1)求 以及
以及
(2)设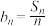 ,证明数列
,证明数列 中不存在不同的三项成等比数列
中不存在不同的三项成等比数列
等差数列
 的前
的前 项和为
项和为 ,
,
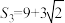
(1)求
 以及
以及
(2)设
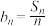 ,证明数列
,证明数列 中不存在不同的三项成等比数列
中不存在不同的三项成等比数列
您最近一年使用:0次