1 . 有三个给定的经过原点的平面,过原点作第四个平面 ,使之与给定的三个平面形成的三个二面角均相等,则这样的
,使之与给定的三个平面形成的三个二面角均相等,则这样的 的个数是( )
的个数是( )
 ,使之与给定的三个平面形成的三个二面角均相等,则这样的
,使之与给定的三个平面形成的三个二面角均相等,则这样的 的个数是( )
的个数是( )| A.0 | B.1 | C.4 | D.以上答案都不对 |
您最近一年使用:0次
名校
解题方法
2 . 在三棱锥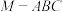 中,下列命题正确的是( )
中,下列命题正确的是( )
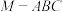 中,下列命题正确的是( )
中,下列命题正确的是( )A.若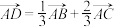 ,则 ,则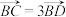 |
B.若G为 的重心,则 的重心,则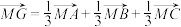 |
C.若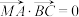 , ,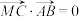 ,则 ,则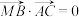 |
D.若三棱锥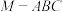 的棱长都为2,P,Q分别为MA,BC中点,则 的棱长都为2,P,Q分别为MA,BC中点,则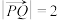 |
您最近一年使用:0次
2020-12-04更新
|
1811次组卷
|
7卷引用:江苏省常州高级中学2020-2021学年高二上学期期中数学试题
江苏省常州高级中学2020-2021学年高二上学期期中数学试题北师大版(2019) 选修第一册 必杀技 第三章 2.2 课时2 空间向量的数量积(已下线)第02讲 空间向量基本定理(教师版)-【帮课堂】(已下线)习题 3-22021年北京大学基础学科招生考试数学试题福建省莆田市第五中学2023-2024学年高二上学期月考(一)数学试卷 (已下线)专题02 空间向量基本定理及其坐标表示压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)
名校
解题方法
3 . 已知抛物线 :
: 的焦点为
的焦点为 ,准线与
,准线与 轴交于
轴交于 点,过点
点,过点 的直线与抛物线
的直线与抛物线 交于
交于 ,
, 两点,且
两点,且 .
.
(1)求抛物线 的方程;
的方程;
(2)设 ,
, 是抛物线
是抛物线 上的不同两点,且
上的不同两点,且 轴,直线
轴,直线 与
与 轴交于
轴交于 点,再在
点,再在 轴上截取线段
轴上截取线段 ,且点
,且点 介于点
介于点 点
点 之间,连接
之间,连接 ,过点
,过点 作直线
作直线 的平行线
的平行线 ,证明
,证明 是抛物线
是抛物线 的切线.
的切线.
 :
: 的焦点为
的焦点为 ,准线与
,准线与 轴交于
轴交于 点,过点
点,过点 的直线与抛物线
的直线与抛物线 交于
交于 ,
, 两点,且
两点,且 .
.(1)求抛物线
 的方程;
的方程;(2)设
 ,
, 是抛物线
是抛物线 上的不同两点,且
上的不同两点,且 轴,直线
轴,直线 与
与 轴交于
轴交于 点,再在
点,再在 轴上截取线段
轴上截取线段 ,且点
,且点 介于点
介于点 点
点 之间,连接
之间,连接 ,过点
,过点 作直线
作直线 的平行线
的平行线 ,证明
,证明 是抛物线
是抛物线 的切线.
的切线.
您最近一年使用:0次
2021-09-01更新
|
1006次组卷
|
5卷引用:广东省佛山市南海区2022届高三上学期8月开学摸底数学试题
广东省佛山市南海区2022届高三上学期8月开学摸底数学试题山西省怀仁市第一中学2022届高三上学期期中数学(理)试题(已下线)专题47 盘点圆锥曲线中的几何证明问题——备战2022年高考数学二轮复习常考点专题突破2021年清华大学语言类保送暨高水平艺术团数学试题(已下线)3.3 抛物线(练习)-高二数学同步精品课堂(苏教版2019选择性必修第一册)
解题方法
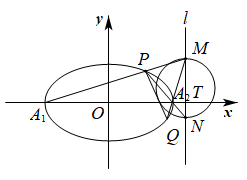
4 . 如图,已知椭圆 的两个焦点分别为
的两个焦点分别为 ,且椭圆与直线
,且椭圆与直线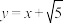 相切.
相切.
(1)求椭圆的方程.
(2)设椭圆的左右顶点分别为 ,若直线
,若直线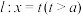 与x轴交于T点,点M为直线l上异于点T的任意一点,直线
与x轴交于T点,点M为直线l上异于点T的任意一点,直线 分别与椭圆交于P,Q两点,连结
分别与椭圆交于P,Q两点,连结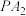 的直线l与交于N点.是否存在t,使得直线
的直线l与交于N点.是否存在t,使得直线 与以
与以 为直径的圆总相切?若存在,求出t;若不存在,请说明理由.
为直径的圆总相切?若存在,求出t;若不存在,请说明理由.
 的两个焦点分别为
的两个焦点分别为 ,且椭圆与直线
,且椭圆与直线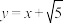 相切.
相切.
(1)求椭圆的方程.
(2)设椭圆的左右顶点分别为
 ,若直线
,若直线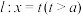 与x轴交于T点,点M为直线l上异于点T的任意一点,直线
与x轴交于T点,点M为直线l上异于点T的任意一点,直线 分别与椭圆交于P,Q两点,连结
分别与椭圆交于P,Q两点,连结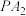 的直线l与交于N点.是否存在t,使得直线
的直线l与交于N点.是否存在t,使得直线 与以
与以 为直径的圆总相切?若存在,求出t;若不存在,请说明理由.
为直径的圆总相切?若存在,求出t;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
5 . 材料:对抛物线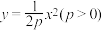 ,定义:点
,定义:点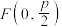 叫做该抛物线的焦点,直线
叫做该抛物线的焦点,直线 叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:
叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:
如图,已知抛物线 的图象与
的图象与 轴交于
轴交于 两点,且过点
两点,且过点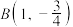 ,
, 的解析式和点A的坐标;
的解析式和点A的坐标;
(2)若将抛物线 的图象向左平移2个单位,再向上平移1个单位得抛物线
的图象向左平移2个单位,再向上平移1个单位得抛物线 的图象.
的图象.
①设 为抛物线
为抛物线 位于第一象限内图象上的任意一点,
位于第一象限内图象上的任意一点, 轴于点
轴于点 ,求
,求 的最小值;
的最小值;
②若过抛物线 的焦点
的焦点 作直线
作直线 ,与抛物线
,与抛物线 交于
交于 两点,再过
两点,再过 两点分别作抛物线的切线,两条切线交于点
两点分别作抛物线的切线,两条切线交于点 ,求
,求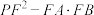 的值.
的值.
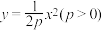 ,定义:点
,定义:点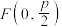 叫做该抛物线的焦点,直线
叫做该抛物线的焦点,直线 叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:
叫做该抛物线的准线,且该抛物线上任意一点到焦点的距离与它到准线的距离相等.运用上述材料解决如下问题:如图,已知抛物线
 的图象与
的图象与 轴交于
轴交于 两点,且过点
两点,且过点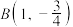 ,
,
 的解析式和点A的坐标;
的解析式和点A的坐标;(2)若将抛物线
 的图象向左平移2个单位,再向上平移1个单位得抛物线
的图象向左平移2个单位,再向上平移1个单位得抛物线 的图象.
的图象.①设
 为抛物线
为抛物线 位于第一象限内图象上的任意一点,
位于第一象限内图象上的任意一点, 轴于点
轴于点 ,求
,求 的最小值;
的最小值;②若过抛物线
 的焦点
的焦点 作直线
作直线 ,与抛物线
,与抛物线 交于
交于 两点,再过
两点,再过 两点分别作抛物线的切线,两条切线交于点
两点分别作抛物线的切线,两条切线交于点 ,求
,求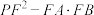 的值.
的值.
您最近一年使用:0次
6 . 过椭圆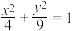 的中心作两条互相垂直的弦
的中心作两条互相垂直的弦 和
和 ,顺次连接
,顺次连接 得一四边形,则该四边形的面积可能为( )
得一四边形,则该四边形的面积可能为( )
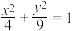 的中心作两条互相垂直的弦
的中心作两条互相垂直的弦 和
和 ,顺次连接
,顺次连接 得一四边形,则该四边形的面积可能为( )
得一四边形,则该四边形的面积可能为( )| A.10 | B.12 | C.14 | D.16 |
您最近一年使用:0次
7 . 已知非负实数x,y满足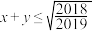 ,求
,求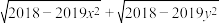 的最小值.
的最小值.
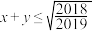 ,求
,求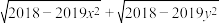 的最小值.
的最小值.
您最近一年使用:0次
2014高三·全国·专题练习
解题方法
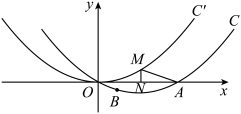
8 . 如图,在平面直角坐标系 中,已知点
中,已知点 分别为椭圆E:
分别为椭圆E: 的左、右焦点,A、B分别是椭圆E的左、右顶点,
的左、右焦点,A、B分别是椭圆E的左、右顶点,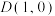 为线段
为线段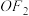 的中点,且
的中点,且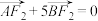 .
.
(1)求椭圆E的方程;
(2)若M为椭圆上的动点(异于A、B),连接 并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为
并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为 、
、 ,试问是否存在常数
,试问是否存在常数 ,使得
,使得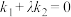 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 中,已知点
中,已知点 分别为椭圆E:
分别为椭圆E: 的左、右焦点,A、B分别是椭圆E的左、右顶点,
的左、右焦点,A、B分别是椭圆E的左、右顶点,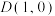 为线段
为线段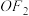 的中点,且
的中点,且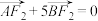 .
.(1)求椭圆E的方程;
(2)若M为椭圆上的动点(异于A、B),连接
 并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为
并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于点P、Q,连接PQ,设直线MN、PQ的斜率存在且分别为 、
、 ,试问是否存在常数
,试问是否存在常数 ,使得
,使得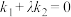 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次



