名校
1 . 17世纪初,约翰•纳皮尔为了简化计算而发明了对数.对数的发明是数学史上的重大事件,恩格斯曾经把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为17世纪的三大数学发明.我们知道,任何一个正实数 可以表示成
可以表示成 的形式,这便是科学记数法,若两边取常用对数,则有
的形式,这便是科学记数法,若两边取常用对数,则有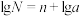 .现给出部分常用对数值(如下表),则可以估计
.现给出部分常用对数值(如下表),则可以估计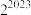 的最高位的数值为( )
的最高位的数值为( )
 可以表示成
可以表示成 的形式,这便是科学记数法,若两边取常用对数,则有
的形式,这便是科学记数法,若两边取常用对数,则有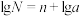 .现给出部分常用对数值(如下表),则可以估计
.现给出部分常用对数值(如下表),则可以估计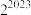 的最高位的数值为( )
的最高位的数值为( )真数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 (近似值) (近似值) | 0.30103 | 0.47712 | 0.60206 | 0.69897 | 0.77815 | 0.84510 | 0.90309 | 0.95424 | 1.000 |
A. | B. | C. | D. |
您最近一年使用:0次
名校
解题方法
2 . 中国南宋大数学家秦九韶提出了“三斜求积术”,即已知三角形三边长求三角形面积的公式:设三角形的三条边长分别为 ,则三角形的面积
,则三角形的面积 可由公式
可由公式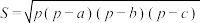 求得,其中
求得,其中 为三角形周长的一半,这个公式也被称为海伦-秦九韶公式.现有一个三角形的边长满足
为三角形周长的一半,这个公式也被称为海伦-秦九韶公式.现有一个三角形的边长满足 ,
, ,则此三角形面积的最大值为
,则此三角形面积的最大值为______ .
 ,则三角形的面积
,则三角形的面积 可由公式
可由公式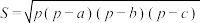 求得,其中
求得,其中 为三角形周长的一半,这个公式也被称为海伦-秦九韶公式.现有一个三角形的边长满足
为三角形周长的一半,这个公式也被称为海伦-秦九韶公式.现有一个三角形的边长满足 ,
, ,则此三角形面积的最大值为
,则此三角形面积的最大值为
您最近一年使用:0次
3 . 德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数 ,被称为狄利克雷函数,其中
,被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则以下关于狄利克雷函数
为有理数集,则以下关于狄利克雷函数 的结论中,正确的是( )
的结论中,正确的是( )
 ,被称为狄利克雷函数,其中
,被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则以下关于狄利克雷函数
为有理数集,则以下关于狄利克雷函数 的结论中,正确的是( )
的结论中,正确的是( )A.函数 满足: 满足: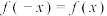 |
B.函数 的值域是 的值域是 |
C.对于任意的 ,都有 ,都有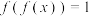 |
D.在 图象上不存在不同的三个点 图象上不存在不同的三个点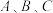 ,使得 ,使得 为等边三角形 为等边三角形 |
您最近一年使用:0次
2024-10-09更新
|
639次组卷
|
2卷引用:湖南省长沙市周南中学2024-2025学年高一上学期第一阶段性测试(10月)数学试题
4 . 祖暅在数学上做出了突出贡献,他提出了体积计算原理:“幂势既同,则积不容异”.这就是“祖暅原理”,用现代语言可以描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.由曲线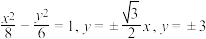 共同围成的图形绕
共同围成的图形绕 轴旋转一周所得几何体的体积为
轴旋转一周所得几何体的体积为 ,则
,则
__________ .
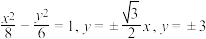 共同围成的图形绕
共同围成的图形绕 轴旋转一周所得几何体的体积为
轴旋转一周所得几何体的体积为 ,则
,则
您最近一年使用:0次
5 . 岳阳楼与湖北武汉黄鹤楼、江西南昌滕王阁并称为“江南三大名楼”,是“中国十大历史文化名楼”之一.小李为测量岳阳楼的高度选取了与底部水平的直线 ,如图,测得
,如图,测得 米,则岳阳楼的高度测量值
米,则岳阳楼的高度测量值 为( )
为( )
 ,如图,测得
,如图,测得 米,则岳阳楼的高度测量值
米,则岳阳楼的高度测量值 为( )
为( )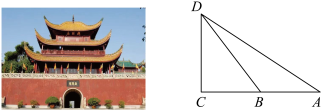
A.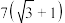 米 米 | B.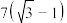 米 米 |
C.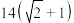 米 米 | D.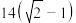 米 米 |
您最近一年使用:0次
名校
解题方法
6 . 冰雹猜想又称考拉兹猜想、角谷猜想、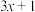 猜想等,其描述为:任一正整数
猜想等,其描述为:任一正整数 ,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为5→16→8→4→2→1,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为( )
,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为5→16→8→4→2→1,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为( )
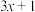 猜想等,其描述为:任一正整数
猜想等,其描述为:任一正整数 ,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为5→16→8→4→2→1,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为( )
,如果是奇数就乘以3再加1,如果是偶数就除以2,反复计算,最终都将会得到数字1.例如:给出正整数5,则进行这种反复运算的过程为5→16→8→4→2→1,即按照这种运算规律进行5次运算后得到1.若从正整数6,7,8,9,10中任取2个数按照上述运算规律进行运算,则运算次数均为奇数的概率为( )A. | B. | C. | D.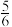 |
您最近一年使用:0次
名校
解题方法
7 . 近年,“人工智能”相关软件以其极高的智能化水平引起国内关注,深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为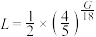 ,其中
,其中 表示每一轮优化时使用的学习率,
表示每一轮优化时使用的学习率, 表示训练迭代轮数,则学习率衰减到0.2及以下所需的训练迭代轮数至少为(参考数据:
表示训练迭代轮数,则学习率衰减到0.2及以下所需的训练迭代轮数至少为(参考数据: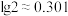 )( )
)( )
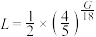 ,其中
,其中 表示每一轮优化时使用的学习率,
表示每一轮优化时使用的学习率, 表示训练迭代轮数,则学习率衰减到0.2及以下所需的训练迭代轮数至少为(参考数据:
表示训练迭代轮数,则学习率衰减到0.2及以下所需的训练迭代轮数至少为(参考数据: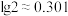 )( )
)( )| A.16 | B.72 | C.74 | D.90 |
您最近一年使用:0次
2024-07-02更新
|
784次组卷
|
4卷引用:湖南省常德市第一中学2025届高三上学期第一次月考数学试题
湖南省常德市第一中学2025届高三上学期第一次月考数学试题浙江省强基(培优)联盟2023-2024学年高二下学期7月学考联考(期末)数学试题(已下线)周测4 基本初等函数 一轮周测卷(提升卷)(已下线)考点14 指数、对数的运算 --高考数学100个黄金考点(2025届)【讲】
名校
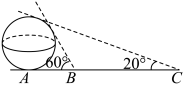
8 . 古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作,也为地图学提供了数学基础,根据刘徽的《重差》测量一个球体建筑的高度,已知点 是球体建筑物与水平地面的接触点(切点),地面上
是球体建筑物与水平地面的接触点(切点),地面上 两点与点
两点与点 在同一条直线上,且在点
在同一条直线上,且在点 的同侧,若在
的同侧,若在 处分别测量球体建筑物的最大仰角为
处分别测量球体建筑物的最大仰角为 和
和 ,且
,且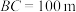 ,则该球体建筑物的高度约为( )
,则该球体建筑物的高度约为( )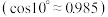
 是球体建筑物与水平地面的接触点(切点),地面上
是球体建筑物与水平地面的接触点(切点),地面上 两点与点
两点与点 在同一条直线上,且在点
在同一条直线上,且在点 的同侧,若在
的同侧,若在 处分别测量球体建筑物的最大仰角为
处分别测量球体建筑物的最大仰角为 和
和 ,且
,且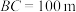 ,则该球体建筑物的高度约为( )
,则该球体建筑物的高度约为( )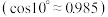
A. | B.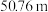 | C. | D.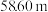 |
您最近一年使用:0次
2024-07-02更新
|
294次组卷
|
2卷引用:湖南省邵阳市第二中学2023-2024学年高一下学期6月期末考试数学试题
9 . 我国古代《九章算术》将上下两个平行平面为矩形的六面体称为“刍童”.如图,在刍童 中,
中,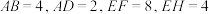 ,平面
,平面 与平面
与平面 之间的距离为3,则此“刍童”的体积为( )
之间的距离为3,则此“刍童”的体积为( )
 中,
中,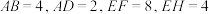 ,平面
,平面 与平面
与平面 之间的距离为3,则此“刍童”的体积为( )
之间的距离为3,则此“刍童”的体积为( )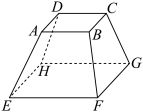
| A.36 | B.46 | C.56 | D.66 |
您最近一年使用:0次
2024-06-25更新
|
480次组卷
|
3卷引用:湖南省益阳市安化县两校联考2023-2024学年高二下学期7月期末自检数学试题
名校
解题方法
10 . 十七世纪法国数学家、被誉为业余数学家之王的皮埃尔・德・费马提出的一个著名的几何问题:“已知一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小”,意大利数学家托里拆利给出了解答,当 的三个内角均小于
的三个内角均小于 时,使得
时,使得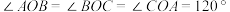 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.已知
时,最大内角的顶点为费马点.已知 ,
, ,
, 分别是
分别是 三个内角
三个内角 ,
, ,
, 的对边,且
的对边,且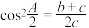 ,若点
,若点 为
为 的费马点,
的费马点,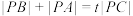 ,则实数
,则实数 的取值范围为
的取值范围为________ .
 的三个内角均小于
的三个内角均小于 时,使得
时,使得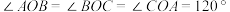 的点
的点 即为费马点;当
即为费马点;当 有一个内角大于或等于
有一个内角大于或等于 时,最大内角的顶点为费马点.已知
时,最大内角的顶点为费马点.已知 ,
, ,
, 分别是
分别是 三个内角
三个内角 ,
, ,
, 的对边,且
的对边,且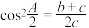 ,若点
,若点 为
为 的费马点,
的费马点,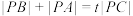 ,则实数
,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
2024-06-20更新
|
232次组卷
|
4卷引用:湖南省邵阳市第二中学2024届高三下学期5月模拟考试数学试题
湖南省邵阳市第二中学2024届高三下学期5月模拟考试数学试题(已下线)第10题 多三角形条件下的解三角形问题(压轴小题)山东省日照市莒县第二中学2024届高三下学期5月月考数学试题(已下线)数学03(全国通用)-新高二上学期数学开学摸底考试卷



