名校
1 . 已知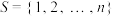 ,
, ,
,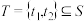 ,记
,记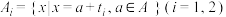 ,用
,用 表示有限集合X的元素个数.
表示有限集合X的元素个数.
(1)若 ,
,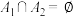 ,分别讨论
,分别讨论 和
和 时,集合T的情况;
时,集合T的情况;
(2)若 ,
,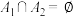 ,求
,求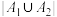 的最大值;
的最大值;
(3)若 ,
,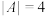 ,则对于任意的A,是否都存在T,使得
,则对于任意的A,是否都存在T,使得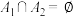 ?说明理由.
?说明理由.
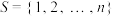 ,
, ,
,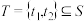 ,记
,记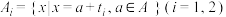 ,用
,用 表示有限集合X的元素个数.
表示有限集合X的元素个数.(1)若
 ,
,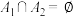 ,分别讨论
,分别讨论 和
和 时,集合T的情况;
时,集合T的情况;(2)若
 ,
,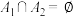 ,求
,求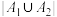 的最大值;
的最大值;(3)若
 ,
,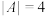 ,则对于任意的A,是否都存在T,使得
,则对于任意的A,是否都存在T,使得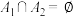 ?说明理由.
?说明理由.
您最近一年使用:0次
名校
解题方法
2 . 设A是正整数集的一个非空子集,如果对于任意 ,都有
,都有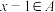 或
或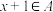 ,则称A为自邻集.记集合
,则称A为自邻集.记集合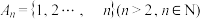 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.
(1)直接写出 的所有自邻集;
的所有自邻集;
(2)若 为偶数且
为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;
(3)若 ,求证:
,求证: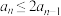 .
.
 ,都有
,都有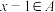 或
或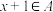 ,则称A为自邻集.记集合
,则称A为自邻集.记集合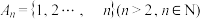 的所有子集中的自邻集的个数为
的所有子集中的自邻集的个数为 .
.(1)直接写出
 的所有自邻集;
的所有自邻集;(2)若
 为偶数且
为偶数且 ,求证:
,求证: 的所有含5个元素的子集中,自邻集的个数是偶数;
的所有含5个元素的子集中,自邻集的个数是偶数;(3)若
 ,求证:
,求证: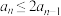 .
.
您最近一年使用:0次
2023-05-28更新
|
706次组卷
|
11卷引用:北京市第二十中学2022-2023学年高二上学期12月月考数学试题
北京市第二十中学2022-2023学年高二上学期12月月考数学试题北京市西城区2021届高三5月二模数学试题北京市第五十七中学2021-2022学年高二上学期期中检测数学试题北京一零一中学2023届高三下学期数学统练四试题北京卷专题02集合(解答题)北京市第一0一中学2022-2023学年高三下学期统练数学试卷(四)(已下线)高一上学期第一次月考解答题压轴题50题专练-举一反三系列北京市北京师范大学第二附属中学2023-2024学年高二上学期期中测试数学试题北京市东城区景山学校2024届高三上学期12月月考数学试题北京市第二中学2023-2024学年高二上学期12月第二学段考试数学试卷(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)
名校
解题方法
3 . 设 为非空集合,定义
为非空集合,定义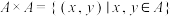 (其中
(其中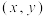 表示有序对),称
表示有序对),称 的任意非空子集
的任意非空子集 为
为 上的一个关系.例如
上的一个关系.例如 时,
时, 与
与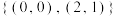 都是
都是 上的关系.设
上的关系.设 为非空集合
为非空集合 上的关系.给出如下定义:①(自反性)若对任意
上的关系.给出如下定义:①(自反性)若对任意 ,有
,有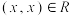 ,则称
,则称 在
在 上是自反的;②(对称性)若对任意
上是自反的;②(对称性)若对任意 ,有
,有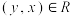 ,则称
,则称 在
在 上是对称的;③(传递性)若对任意
上是对称的;③(传递性)若对任意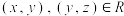 ,有
,有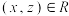 ,则称
,则称 在
在 上是传递的.如果
上是传递的.如果 上关系
上关系 同时满足上述3条性质,则称
同时满足上述3条性质,则称 为
为 上的等价关系.任给集合
上的等价关系.任给集合 ,定义
,定义 为
为 .
.
(1)若 ,问:
,问: 上关系有多少个?
上关系有多少个? 上等价关系有多少个?(不必说明理由)
上等价关系有多少个?(不必说明理由)
(2)若集合 有
有 个元素
个元素 ,
, 的非空子集
的非空子集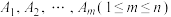 两两交集为空集,且
两两交集为空集,且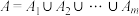 ,求证:
,求证: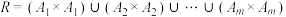 为
为 上的等价关系.
上的等价关系.
(3)若集合 有
有 个元素
个元素 ,问:对
,问:对 上的任意等价关系
上的任意等价关系 ,是否存在
,是否存在 的非空子集
的非空子集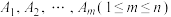 ,其中任意两个交集为空集,且
,其中任意两个交集为空集,且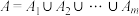 ,使得
,使得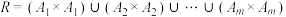 ?请判断并说明理由.
?请判断并说明理由.
 为非空集合,定义
为非空集合,定义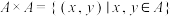 (其中
(其中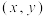 表示有序对),称
表示有序对),称 的任意非空子集
的任意非空子集 为
为 上的一个关系.例如
上的一个关系.例如 时,
时, 与
与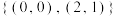 都是
都是 上的关系.设
上的关系.设 为非空集合
为非空集合 上的关系.给出如下定义:①(自反性)若对任意
上的关系.给出如下定义:①(自反性)若对任意 ,有
,有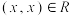 ,则称
,则称 在
在 上是自反的;②(对称性)若对任意
上是自反的;②(对称性)若对任意 ,有
,有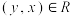 ,则称
,则称 在
在 上是对称的;③(传递性)若对任意
上是对称的;③(传递性)若对任意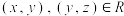 ,有
,有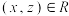 ,则称
,则称 在
在 上是传递的.如果
上是传递的.如果 上关系
上关系 同时满足上述3条性质,则称
同时满足上述3条性质,则称 为
为 上的等价关系.任给集合
上的等价关系.任给集合 ,定义
,定义 为
为 .
.(1)若
 ,问:
,问: 上关系有多少个?
上关系有多少个? 上等价关系有多少个?(不必说明理由)
上等价关系有多少个?(不必说明理由)(2)若集合
 有
有 个元素
个元素 ,
, 的非空子集
的非空子集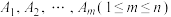 两两交集为空集,且
两两交集为空集,且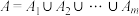 ,求证:
,求证: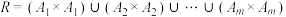 为
为 上的等价关系.
上的等价关系.(3)若集合
 有
有 个元素
个元素 ,问:对
,问:对 上的任意等价关系
上的任意等价关系 ,是否存在
,是否存在 的非空子集
的非空子集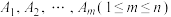 ,其中任意两个交集为空集,且
,其中任意两个交集为空集,且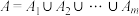 ,使得
,使得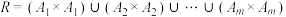 ?请判断并说明理由.
?请判断并说明理由.
您最近一年使用:0次
名校
解题方法
4 . 设自然数 ,若由n个不同的正整数
,若由n个不同的正整数 ,
, ,…,
,…, 构成的集合
构成的集合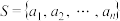 满足:对集合S的任何两个不同的非空子集A、B,A中所有元素之和与B中所有元素之和均不相等,则称集合S具有性质P.
满足:对集合S的任何两个不同的非空子集A、B,A中所有元素之和与B中所有元素之和均不相等,则称集合S具有性质P.
(1)试分别判断在集合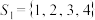 与
与 是否具有性质P,不必说明理由;
是否具有性质P,不必说明理由;
(2)已知集合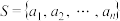 具有性质P.
具有性质P.
①记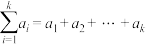 ,求证:对于任意正整数
,求证:对于任意正整数 ,都有
,都有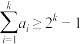 ;
;
②令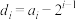 ,
,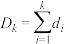 ,求证:
,求证: ;
;
(3)在(2)的条件下,求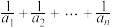 的最大值.
的最大值.
 ,若由n个不同的正整数
,若由n个不同的正整数 ,
, ,…,
,…, 构成的集合
构成的集合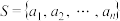 满足:对集合S的任何两个不同的非空子集A、B,A中所有元素之和与B中所有元素之和均不相等,则称集合S具有性质P.
满足:对集合S的任何两个不同的非空子集A、B,A中所有元素之和与B中所有元素之和均不相等,则称集合S具有性质P.(1)试分别判断在集合
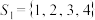 与
与 是否具有性质P,不必说明理由;
是否具有性质P,不必说明理由;(2)已知集合
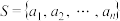 具有性质P.
具有性质P.①记
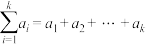 ,求证:对于任意正整数
,求证:对于任意正整数 ,都有
,都有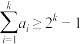 ;
;②令
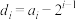 ,
,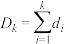 ,求证:
,求证: ;
;(3)在(2)的条件下,求
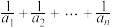 的最大值.
的最大值.
您最近一年使用:0次
名校
5 . 已知 ,对于有限集
,对于有限集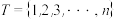 ,令
,令 表示集合
表示集合 中元素的个数.例如:当
中元素的个数.例如:当 时,
时, ,
, .
.
(1)当 时,请直接写出集合
时,请直接写出集合 的子集的个数;
的子集的个数;
(2)当 时,
时, ,
, 都是集合
都是集合 的子集(
的子集( ,
, 可以相同),并且
可以相同),并且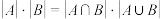 .求满足条件的有序集合对
.求满足条件的有序集合对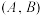 的个数;
的个数;
(3)假设存在集合 、
、 具有以下性质:将1,1,2,2,··,
具有以下性质:将1,1,2,2,··, ,
, .这
.这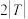 个整数按某种次序排成一列,使得在这个序列中,对于任意
个整数按某种次序排成一列,使得在这个序列中,对于任意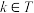 ,
, 与
与 之间恰好排列
之间恰好排列 个整数.证明:
个整数.证明: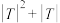 是4的倍数.
是4的倍数.
 ,对于有限集
,对于有限集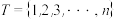 ,令
,令 表示集合
表示集合 中元素的个数.例如:当
中元素的个数.例如:当 时,
时, ,
, .
.(1)当
 时,请直接写出集合
时,请直接写出集合 的子集的个数;
的子集的个数;(2)当
 时,
时, ,
, 都是集合
都是集合 的子集(
的子集( ,
, 可以相同),并且
可以相同),并且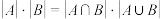 .求满足条件的有序集合对
.求满足条件的有序集合对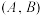 的个数;
的个数;(3)假设存在集合
 、
、 具有以下性质:将1,1,2,2,··,
具有以下性质:将1,1,2,2,··, ,
, .这
.这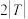 个整数按某种次序排成一列,使得在这个序列中,对于任意
个整数按某种次序排成一列,使得在这个序列中,对于任意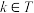 ,
, 与
与 之间恰好排列
之间恰好排列 个整数.证明:
个整数.证明: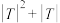 是4的倍数.
是4的倍数.
您最近一年使用:0次
名校
6 . 设 为正整数,集合
为正整数,集合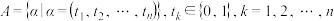 .对于集合
.对于集合 中的任意元素
中的任意元素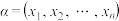 和
和 ,定义
,定义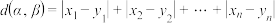 .
.
(1)当 时,若
时,若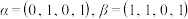 ,直接写出所有使
,直接写出所有使 同时成立的
同时成立的 的元素
的元素 ;
;
(2)当 时,设
时,设 是
是 的子集,且满足:对于
的子集,且满足:对于 中的任意两个不同元素
中的任意两个不同元素 .求集合
.求集合 中元素个数的最大值;
中元素个数的最大值;
(3)给定不小于2的 ,设
,设 是
是 的子集,且满足:对于
的子集,且满足:对于 中的任意两个不同的元素
中的任意两个不同的元素 ,写出一个集合
,写出一个集合 ,使其元素个数最多,并说明理由.
,使其元素个数最多,并说明理由.
 为正整数,集合
为正整数,集合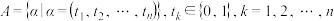 .对于集合
.对于集合 中的任意元素
中的任意元素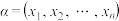 和
和 ,定义
,定义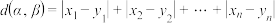 .
.(1)当
 时,若
时,若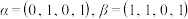 ,直接写出所有使
,直接写出所有使 同时成立的
同时成立的 的元素
的元素 ;
;(2)当
 时,设
时,设 是
是 的子集,且满足:对于
的子集,且满足:对于 中的任意两个不同元素
中的任意两个不同元素 .求集合
.求集合 中元素个数的最大值;
中元素个数的最大值;(3)给定不小于2的
 ,设
,设 是
是 的子集,且满足:对于
的子集,且满足:对于 中的任意两个不同的元素
中的任意两个不同的元素 ,写出一个集合
,写出一个集合 ,使其元素个数最多,并说明理由.
,使其元素个数最多,并说明理由.
您最近一年使用:0次
名校
7 . 含有有限个元素的数集,定义“元素和”如下:把集合中的各数相加;定义“交替和”如下:把集合中的数按从大到小的顺序排列,然后从最大的数开始交替地加减各数.例如{4,6,9}的元素和是4+6+9=19;交替和是9-6+4=7;而{5}的元素和与交替和都是5.
(1)写出集合{1,2,3}的所有非空子集的交替和的总和;
(2)已知集合 ,根据提示解决问题.
,根据提示解决问题.
①求集合 所有非空子集的元素和的总和;
所有非空子集的元素和的总和;
提示:方法1: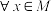 ,先求出
,先求出 在集合
在集合 的非空子集中一共出现多少次,进而可求出集合
的非空子集中一共出现多少次,进而可求出集合 所有非空子集的元素和的总和;方法2:如果我们知道了集合{1,2,3,4,5}的所有非空子集的元素和的总和为
所有非空子集的元素和的总和;方法2:如果我们知道了集合{1,2,3,4,5}的所有非空子集的元素和的总和为 ,可以用
,可以用 表示出
表示出 的非空子集的元素和的总和,递推可求出集合
的非空子集的元素和的总和,递推可求出集合 所有非空子集的元素和的总和.
所有非空子集的元素和的总和.
②求集合 所有非空子集的交替和的总和.
所有非空子集的交替和的总和.
(1)写出集合{1,2,3}的所有非空子集的交替和的总和;
(2)已知集合
 ,根据提示解决问题.
,根据提示解决问题.①求集合
 所有非空子集的元素和的总和;
所有非空子集的元素和的总和;提示:方法1:
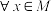 ,先求出
,先求出 在集合
在集合 的非空子集中一共出现多少次,进而可求出集合
的非空子集中一共出现多少次,进而可求出集合 所有非空子集的元素和的总和;方法2:如果我们知道了集合{1,2,3,4,5}的所有非空子集的元素和的总和为
所有非空子集的元素和的总和;方法2:如果我们知道了集合{1,2,3,4,5}的所有非空子集的元素和的总和为 ,可以用
,可以用 表示出
表示出 的非空子集的元素和的总和,递推可求出集合
的非空子集的元素和的总和,递推可求出集合 所有非空子集的元素和的总和.
所有非空子集的元素和的总和.②求集合
 所有非空子集的交替和的总和.
所有非空子集的交替和的总和.
您最近一年使用:0次
2021-10-12更新
|
770次组卷
|
4卷引用:第01讲 集合的概念及基本关系(3大考点10种解题方法)-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)
(已下线)第01讲 集合的概念及基本关系(3大考点10种解题方法)-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)江苏省南京外国语学校2021-2022学年高一上学期10月月考数学试题(已下线)专题02 集合与常用逻辑用语常考压轴题型-2021-2022学年高一《新题速递·数学》(人教A版2019)(已下线)专题01 集合与常用逻辑用语3-寒假作业单元合订本
名校
8 . 设集合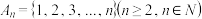 ,集合
,集合 ,如果对于任意元素
,如果对于任意元素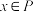 ,都有
,都有 或
或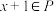 ,则称集合
,则称集合 为
为 的自邻集.记
的自邻集.记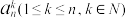 为集合
为集合 的所有自邻集中最大元素为
的所有自邻集中最大元素为 的集合的个数.
的集合的个数.
(1)直接判断集合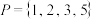 和
和 是否为
是否为 的自邻集;
的自邻集;
(2)比较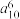 和
和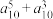 的大小,并说明理由;
的大小,并说明理由;
(3)当 时,求证:
时,求证: .
.
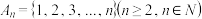 ,集合
,集合 ,如果对于任意元素
,如果对于任意元素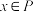 ,都有
,都有 或
或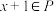 ,则称集合
,则称集合 为
为 的自邻集.记
的自邻集.记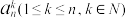 为集合
为集合 的所有自邻集中最大元素为
的所有自邻集中最大元素为 的集合的个数.
的集合的个数.(1)直接判断集合
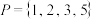 和
和 是否为
是否为 的自邻集;
的自邻集;(2)比较
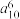 和
和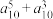 的大小,并说明理由;
的大小,并说明理由;(3)当
 时,求证:
时,求证: .
.
您最近一年使用:0次
2021-07-15更新
|
895次组卷
|
7卷引用:第1章 集合与常用逻辑用语(基础、典型、新文化、压轴)分类专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)
(已下线)第1章 集合与常用逻辑用语(基础、典型、新文化、压轴)分类专项训练-2022-2023学年高一数学考试满分全攻略(人教A版2019必修第一册)北京市八一学校2020-2021学年高一下学期期末数学试题(已下线)1.2 集合间的基本关系-2021-2022学年高一数学尖子生同步培优题典(人教A版2019必修第一册)(已下线)期末重难点突破专题01-【尖子生专用】2021-2022学年高一数学考点培优训练(人教A版2019必修第一册)(已下线)高一上学期期中考试解答题压轴题50题专练-举一反三系列重庆市万州第二高级中学2023-2024学年高一上学期10月月考数学试题 (已下线)专题01 集合与常用逻辑用语3-寒假作业单元合订本
名校
9 . 已知集合 是集合
是集合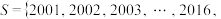
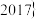 的一个含有
的一个含有 个元素的子集.
个元素的子集.
(Ⅰ)当 时,
时,
设
(i)写出方程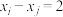 的解
的解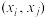 ;
;
(ii)若方程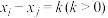 至少有三组不同的解,写出
至少有三组不同的解,写出 的所有可能取值.
的所有可能取值.
(Ⅱ)证明:对任意一个 ,存在正整数
,存在正整数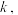 使得方程
使得方程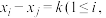
 至少有三组不同的解.
至少有三组不同的解.
 是集合
是集合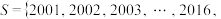
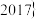 的一个含有
的一个含有 个元素的子集.
个元素的子集.(Ⅰ)当
 时,
时,设

(i)写出方程
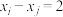 的解
的解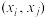 ;
;(ii)若方程
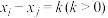 至少有三组不同的解,写出
至少有三组不同的解,写出 的所有可能取值.
的所有可能取值.(Ⅱ)证明:对任意一个
 ,存在正整数
,存在正整数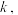 使得方程
使得方程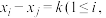
 至少有三组不同的解.
至少有三组不同的解.
您最近一年使用:0次
2018-03-31更新
|
1347次组卷
|
6卷引用:北京市一零一中学2022届高三3月数学统练试题



