名校
1 . 现定义如下:当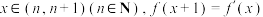 ,则称
,则称 为延展函数,当
为延展函数,当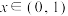 时,
时,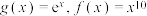 均为延展函数,给定以下两个命题
均为延展函数,给定以下两个命题
①存在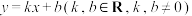 ,与
,与 有无穷个交点;
有无穷个交点;
②存在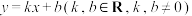 ,与
,与 有无穷个交点;
有无穷个交点;
则下面选项正确的是( )
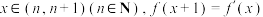 ,则称
,则称 为延展函数,当
为延展函数,当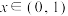 时,
时,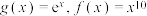 均为延展函数,给定以下两个命题
均为延展函数,给定以下两个命题①存在
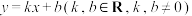 ,与
,与 有无穷个交点;
有无穷个交点;②存在
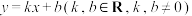 ,与
,与 有无穷个交点;
有无穷个交点;则下面选项正确的是( )
| A.①是真命题,②是真命题 | B.①是假命题,②是假命题 |
| C.①是真命题,②是假命题 | D.①是假命题,②是真命题 |
您最近一年使用:0次
解题方法
2 . 德国数学家狄利克雷在数学领域成就显著,函数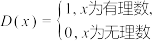 被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①
被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①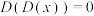 ;②对任意
;②对任意 ,恒有
,恒有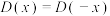 成立;③任取一个不为0的有理数
成立;③任取一个不为0的有理数 ,
,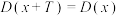 对任意实数
对任意实数 均成立;④存在三个点
均成立;④存在三个点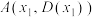 ,
,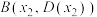 ,
,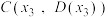 ,使得
,使得 为等边三角形.其中真命题的序号为( )
为等边三角形.其中真命题的序号为( )
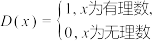 被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①
被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①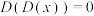 ;②对任意
;②对任意 ,恒有
,恒有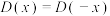 成立;③任取一个不为0的有理数
成立;③任取一个不为0的有理数 ,
,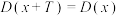 对任意实数
对任意实数 均成立;④存在三个点
均成立;④存在三个点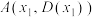 ,
,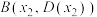 ,
,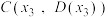 ,使得
,使得 为等边三角形.其中真命题的序号为( )
为等边三角形.其中真命题的序号为( )| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
您最近一年使用:0次
名校
3 . 定义:如果曲线段 可以一笔画出,那么称曲线段
可以一笔画出,那么称曲线段 为
为单轨道曲线 ,比如圆、椭圆都是单轨道曲线;如果曲线段 由两条单轨道曲线构成,那么称曲线段
由两条单轨道曲线构成,那么称曲线段 为
为双轨道曲线 .对于曲线 有如下命题:
有如下命题: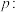 存在常数
存在常数 ,使得曲线
,使得曲线 为单轨道曲线;
为单轨道曲线; 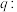 存在常数
存在常数 ,使得曲线
,使得曲线 为双轨道曲线.下列判断正确的是( ).
为双轨道曲线.下列判断正确的是( ).
 可以一笔画出,那么称曲线段
可以一笔画出,那么称曲线段 为
为 由两条单轨道曲线构成,那么称曲线段
由两条单轨道曲线构成,那么称曲线段 为
为 有如下命题:
有如下命题: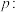 存在常数
存在常数 ,使得曲线
,使得曲线 为单轨道曲线;
为单轨道曲线; 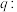 存在常数
存在常数 ,使得曲线
,使得曲线 为双轨道曲线.下列判断正确的是( ).
为双轨道曲线.下列判断正确的是( ).A. 和 和 均为真命题 均为真命题 | B. 和 和 均为假命题 均为假命题 |
C. 为真命题, 为真命题, 为假命题 为假命题 | D. 为假命题, 为假命题, 为真命题 为真命题 |
您最近一年使用:0次
2023-12-13更新
|
771次组卷
|
9卷引用:上海市青浦区2024届高三上学期期终学业质量调研数学试题
上海市青浦区2024届高三上学期期终学业质量调研数学试题上海市吴淞中学2023-2024学年高二上学期期末质量检测数学试卷上海市同济大学第一附属中学2023-2024学年高二上学期期末考试数学试卷(已下线)第1章 坐标平面上的直线 (压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)(已下线)2.5 曲线与方程(五大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)(已下线)第2章 圆锥曲线(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)(已下线)专题07 解析几何(三大类型题综合)15区新题速递(已下线)专题01 集合(15区真题速递)(已下线)专题03 圆 曲线与方程(九大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)
名校
4 . 若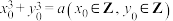 ,则称
,则称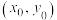 是关于x,y的方程
是关于x,y的方程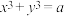 的整数解.关于该方程,下列判断
的整数解.关于该方程,下列判断错误 的是( )
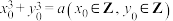 ,则称
,则称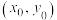 是关于x,y的方程
是关于x,y的方程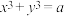 的整数解.关于该方程,下列判断
的整数解.关于该方程,下列判断A.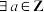 ,方程 ,方程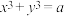 有无限组整数解 有无限组整数解 |
B.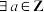 ,方程 ,方程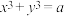 有且只有两组整数解 有且只有两组整数解 |
C.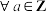 ,方程 ,方程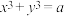 至少有一组整数解 至少有一组整数解 |
D.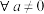 ,方程 ,方程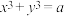 至多有有限组整数解 至多有有限组整数解 |
您最近一年使用:0次
名校
5 . 曲线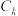 :
: ,下列两个命题:
,下列两个命题:
命题甲:当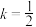 时,曲线与坐标轴围成的面积小于128;
时,曲线与坐标轴围成的面积小于128;
命题乙:当k=2n, 时,曲线围成的面积总大于4;
时,曲线围成的面积总大于4;
下面说法正确的是( )
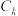 :
: ,下列两个命题:
,下列两个命题:命题甲:当
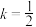 时,曲线与坐标轴围成的面积小于128;
时,曲线与坐标轴围成的面积小于128;命题乙:当k=2n,
 时,曲线围成的面积总大于4;
时,曲线围成的面积总大于4;下面说法正确的是( )
| A.甲是真命题,乙是真命题 | B.甲是真命题,乙是假命题 |
| C.甲是假命题,乙是真命题 | D.甲是假命题,乙是假命题 |
您最近一年使用:0次
2023-06-05更新
|
948次组卷
|
5卷引用:上海市大同中学2023届高三三模数学试题
上海市大同中学2023届高三三模数学试题上海市行知中学2024届高三上学期10月月考数学试题(已下线)2.5 曲线与方程(五大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)(已下线)第2章 圆锥曲线(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第一册)(已下线)期末测试卷01(测试范围:第1-8章)-备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)
6 . 已知平面上三点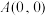 ,
, ,
, ,若动点P满足
,若动点P满足 ,有以下两个命题:①三角形APB面积的最大值为1;②
,有以下两个命题:①三角形APB面积的最大值为1;②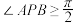 ,则( )
,则( )
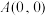 ,
, ,
, ,若动点P满足
,若动点P满足 ,有以下两个命题:①三角形APB面积的最大值为1;②
,有以下两个命题:①三角形APB面积的最大值为1;②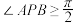 ,则( )
,则( )| A.①为真命题,②为真命题 | B.①为真命题,②为假命题 |
| C.①为假命题,②为真命题 | D.①为假命题,②为假命题 |
您最近一年使用:0次
名校
7 . 对于圆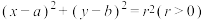 上任意一点
上任意一点 ,当
,当 时,
时, 的值与
的值与 ,
, 无关,有下列结论:
无关,有下列结论:
①点 的轨迹是一个圆; ②点
的轨迹是一个圆; ②点 的轨迹是一条直线;
的轨迹是一条直线;
③当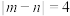 时,
时, 有最大值
有最大值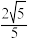 ; ④当
; ④当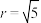 ,
, 时,
时,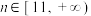 .
.
其中正确的个数是( )
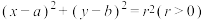 上任意一点
上任意一点 ,当
,当 时,
时, 的值与
的值与 ,
, 无关,有下列结论:
无关,有下列结论:①点
 的轨迹是一个圆; ②点
的轨迹是一个圆; ②点 的轨迹是一条直线;
的轨迹是一条直线;③当
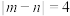 时,
时, 有最大值
有最大值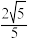 ; ④当
; ④当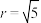 ,
, 时,
时,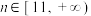 .
.其中正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2023-01-14更新
|
1080次组卷
|
7卷引用:上海市育才中学2022-2023学年高二上学期期末数学试题
上海市育才中学2022-2023学年高二上学期期末数学试题(已下线)高二上学期期中考试选择题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)江苏省扬州市新华中学2023-2024学年高二上学期10月月考数学试题上海市闵行区闵行中学2024届高三上学期12月月考数学试题(已下线)第2章 圆锥曲线 单元综合检测(难点)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)上海市杨浦高级中学2023-2024学年高二下学期期中考试数学试卷(已下线)专题03 圆 曲线与方程(九大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)
8 . 设集合 是集合
是集合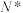 的子集,对于
的子集,对于 ,定义
,定义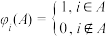 ,给出下列三个结论:①存在
,给出下列三个结论:①存在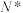 的两个不同子集
的两个不同子集 ,使得任意
,使得任意 都满足
都满足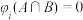 且
且 ;②任取
;②任取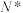 的两个不同子集
的两个不同子集 ,对任意
,对任意 都有
都有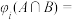
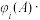
 ;③任取
;③任取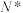 的两个不同子集
的两个不同子集 ,对任意
,对任意 都有
都有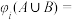
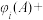
 ;其中,所有正确结论的序号是( )
;其中,所有正确结论的序号是( )
 是集合
是集合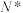 的子集,对于
的子集,对于 ,定义
,定义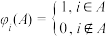 ,给出下列三个结论:①存在
,给出下列三个结论:①存在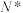 的两个不同子集
的两个不同子集 ,使得任意
,使得任意 都满足
都满足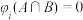 且
且 ;②任取
;②任取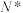 的两个不同子集
的两个不同子集 ,对任意
,对任意 都有
都有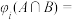
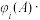
 ;③任取
;③任取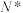 的两个不同子集
的两个不同子集 ,对任意
,对任意 都有
都有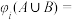
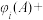
 ;其中,所有正确结论的序号是( )
;其中,所有正确结论的序号是( )| A.①② | B.②③ | C.①③ | D.①②③ |
您最近一年使用:0次
2020-02-09更新
|
2404次组卷
|
14卷引用:2020届北京市海淀区高三上学期期中数学试题
2020届北京市海淀区高三上学期期中数学试题北京交通大学附属中学2020-2021学年高一上学期期中练习数学试题(已下线)思想05 第三篇 思想方法(测试卷)-2021年高考二轮复习讲练测(浙江专用)北京市海淀区2021届高三模拟试题(一)(已下线)考点突破01 集合与常用逻辑用语-备战2022年高考数学一轮复习培优提升精炼(新高考地区专用)(已下线)考点47 推理与证明-备战2022年高考数学(文)一轮复习考点帮北京市中关村中学2021-2022学年高一上学期期中阶段学情调研数学试题(已下线)专题01 集合-备战2022年高考数学(文)母题题源解密(全国乙卷)(已下线)专题02 集合与常用逻辑用语常考压轴题型-2021-2022学年高一《新题速递·数学》(人教A版2019)(已下线)专题1-2 简易逻辑题型归类-3北京市景山学校2022届高三上学期期中考试数学试题中国人民大学附属中学2023-2024学年高一上学期数学统练(一)试题(已下线)第1章 集合与常用逻辑用语-【优化数学】单元测试能力卷(人教B版2019)北京市延庆区第一中学2023-2024学年高一上学期10月月考数学试题
2012·河南郑州·一模
真题
解题方法
9 . 在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k丨n∈Z},k=0,1,2,3,4.给出如下四个结论:
①2011∈[1];
②﹣3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4];
④“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.
其中,正确结论的个数是
①2011∈[1];
②﹣3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4];
④“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.
其中,正确结论的个数是
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2019-01-30更新
|
1581次组卷
|
8卷引用:2011年普通高等学校招生全国统一考试文科数学(福建卷)
2011年普通高等学校招生全国统一考试文科数学(福建卷)(已下线)2012届河南省中原六校高三第一次联考理科数学试卷【全国市级联考】河南省南阳市2017-2018学年高二下学期期中考试数学(文)试题(已下线)专题01 集合概念与运算-十年(2011-2020)高考真题数学分项(已下线)专题06集合的运算2020年初升高数学无忧衔接(沪教版)(已下线)考点05 函数的基本性质-备战2022年高考数学(文)一轮复习考点帮北京市第四十四中学2022-2023学年高一上学期10月月考数学试题(已下线)压轴题高等数学背景下新定义题(九省联考第19题模式)练
9-10高二下·福建龙岩·期中
名校
10 . 对于直角坐标平面内的任意两点 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: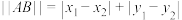 .给出下列三个命题:
.给出下列三个命题:
①若点 在线段
在线段 上,则
上,则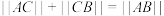 ;
;
②在 中,若
中,若 ,则
,则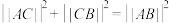 ;
;
③在 中,
中,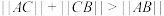 ,其中真命题的个数为
,其中真命题的个数为
 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: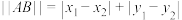 .给出下列三个命题:
.给出下列三个命题:①若点
 在线段
在线段 上,则
上,则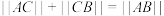 ;
;②在
 中,若
中,若 ,则
,则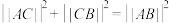 ;
;③在
 中,
中,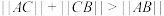 ,其中真命题的个数为
,其中真命题的个数为A. | B. | C. | D. |
您最近一年使用:0次
2018-04-04更新
|
935次组卷
|
10卷引用:2010年福建省上杭一中高二第二学期半期考试数学(理科)试题
(已下线)2010年福建省上杭一中高二第二学期半期考试数学(理科)试题(已下线)2012-2013年山东济宁泗水一中高二12月质量检测理科数学试卷(已下线)2012-2013学年山东省济宁市高二上学期期末理科数学(已下线)2013届广东省广宁县广宁中学高三2月月考理科数学试卷2015-2016学年广东省英德市一中高二上学期第一次月考理科数学试卷北京市北京八中2018届高三第二次月考数学理科试题上海市杨思高级中学2020-2021学年高一上学期期中数学试题人教B版(2019) 选修第一册 过关检测 第二章 2.1坐标法上海市上海交通大学附属中学2022届高三下学期期中数学试题(已下线)专题01 集合与不等式必考题型分类训练-3



