【巩固卷】第5章测评卷 单元测试A-沪教版(2020)必修第一册
上海
高一
单元测试
2024-07-12
139次
整体难度:
容易
考查范围:
函数与导数、集合与常用逻辑用语
一、填空题 添加题型下试题
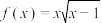 ,
,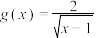 ,则
,则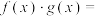
【知识点】 已知函数类型求解析式解读 解析法表示函数解读 函数的和与积
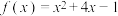 的单调增区间是
的单调增区间是【知识点】 求函数的单调区间 判断二次函数的单调性和求解单调区间
 是定义在R上偶函数,且当
是定义在R上偶函数,且当 ,
, ,则
,则
【知识点】 函数奇偶性的应用
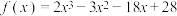 在区间
在区间 内的零点时,取
内的零点时,取 的中点
的中点 ,则
,则 的下一个有零点的区间是
的下一个有零点的区间是【知识点】 二分法求方程近似解的过程
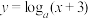 (
( 且
且 )的反函数的图像都过点
)的反函数的图像都过点 ,则点
,则点 的坐标是
的坐标是【知识点】 对数型函数图象过定点问题 反函数的性质应用
 是定义在区间
是定义在区间 上的严格增函数.若
上的严格增函数.若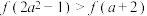 ,则a的取值范围是
,则a的取值范围是【知识点】 根据函数的单调性解不等式
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,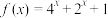 ,则当
,则当 时,
时, 的值域为
的值域为【知识点】 求指数型复合函数的值域 分段函数的值域或最值 奇偶函数对称性的应用
 的定义域为
的定义域为 ,
,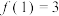 ,对任意两个不等的实数
,对任意两个不等的实数 、
、 都有
都有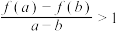 ,则不等式
,则不等式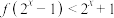 的解集为
的解集为【知识点】 根据函数的单调性解不等式 由指数函数的单调性解不等式
 ,
,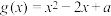 ,如果对任意的实数
,如果对任意的实数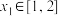 ,任意的实数
,任意的实数 ,不等式
,不等式 恒成立,则实数a的取值范围为
恒成立,则实数a的取值范围为二、单选题 添加题型下试题
 的偶函数是( )
的偶函数是( )A. | B.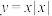 |
C.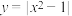 | D.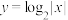 |
【知识点】 函数奇偶性的定义与判断解读
 在
在 上是增函数,且
上是增函数,且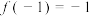 ,若对所有的
,若对所有的 及任意的
及任意的 都满足
都满足 ,则
,则 的取值范围是( )
的取值范围是( )A. | B.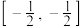 |
C.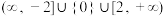 | D.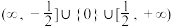 |
【知识点】 根据函数的最值求参数 根据函数的单调性解不等式 由函数奇偶性解不等式
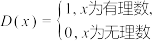 被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①
被称为狄利克雷函数.关于狄利克雷函数有如下四个命题:①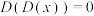 ;②对任意
;②对任意 ,恒有
,恒有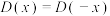 成立;③任取一个不为0的有理数
成立;③任取一个不为0的有理数 ,
,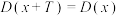 对任意实数
对任意实数 均成立;④存在三个点
均成立;④存在三个点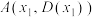 ,
,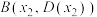 ,
,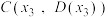 ,使得
,使得 为等边三角形.其中真命题的序号为( )
为等边三角形.其中真命题的序号为( )| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
三、解答题 添加题型下试题
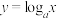 在
在 上是严格减函数,求函数
上是严格减函数,求函数 在
在 上的最值.
上的最值.
【知识点】 求二次函数的值域或最值 由对数(型)的单调性求参数
 ,
,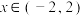 .
.(1)求
 的值.
的值.(2)用定义证明函数
 在
在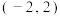 上为增函数.
上为增函数.
【知识点】 求函数值解读 定义法判断或证明函数的单调性解读
(1)求函数f(x)的解析式;
(2)当x∈[1,2]时,求f(x)的值域;
(3)若F(x)=f(x)-f(-x),试判断F(x)的奇偶性,并证明你的结论.
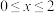 时,
时, ,当
,当 时,
时, 的图象是顶点为
的图象是顶点为 且过点
且过点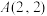 的抛物线的一部分.
的抛物线的一部分.(1)求函数
 在
在 上的解析式;
上的解析式;(2)在图中的直角坐标系中画出函数
 的图象;
的图象;(3)写出函数
 的值域和单调区间.
的值域和单调区间.
 (百件)与时间第
(百件)与时间第 天的关系如下表所示:
天的关系如下表所示:第 天 天 | 1 | 3 | 10 |  | 30 |
日销售量 (百件) (百件) | 2 | 3 | 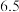 |  |  |
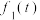 (元)与时间第
(元)与时间第 天的函数关系式为
天的函数关系式为 ,且
,且 为整数
为整数 ,而后15天此商品每天每件的利润
,而后15天此商品每天每件的利润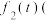 元
元 与时间第
与时间第 天的函数关系式为
天的函数关系式为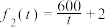 (
(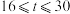 ,且
,且 为整数).
为整数).(1)现给出以下两类函数模型:①
 (
(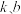 为常数);②
为常数);②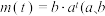 为常数,
为常数, 且
且 .分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;
.分析表格中的数据,请说明哪类函数模型更合适,并求出该函数解析式;(2)若这30天内该公司此商品的日销售利润始终不能超过4万元,则考虑转型.请判断该公司是否需要转型?并说明理由.
试卷分析
导出试卷题型(共 21题)
试卷难度
细目表分析
| 题号 | 难度系数 | 详细知识点 | 备注 |
| 一、填空题 | |||
| 1 | 0.85 | 具体函数的定义域 | 单空题 |
| 2 | 0.65 | 求分段函数值 | 单空题 |
| 3 | 0.94 | 已知函数类型求解析式 解析法表示函数 函数的和与积 | 单空题 |
| 4 | 0.94 | 求函数的单调区间 判断二次函数的单调性和求解单调区间 | 单空题 |
| 5 | 0.94 | 函数奇偶性的应用 | 单空题 |
| 6 | 0.94 | 二分法求方程近似解的过程 | 单空题 |
| 7 | 0.94 | 对数型函数图象过定点问题 反函数的性质应用 | 单空题 |
| 8 | 0.85 | 根据函数的单调性解不等式 | 单空题 |
| 9 | 0.85 | 求指数型复合函数的值域 分段函数的值域或最值 奇偶函数对称性的应用 | 单空题 |
| 10 | 0.85 | 函数奇偶性的应用 函数对称性的应用 | 单空题 |
| 11 | 0.65 | 根据函数的单调性解不等式 由指数函数的单调性解不等式 | 单空题 |
| 12 | 0.65 | 求二次函数的值域或最值 求指数函数在区间内的值域 函数不等式恒成立问题 | 单空题 |
| 二、单选题 | |||
| 13 | 0.85 | 函数奇偶性的定义与判断 | |
| 14 | 0.85 | 函数图像的识别 | |
| 15 | 0.4 | 根据函数的最值求参数 根据函数的单调性解不等式 由函数奇偶性解不等式 | |
| 16 | 0.4 | 判断命题的真假 函数基本性质的综合应用 函数奇偶性的定义与判断 | |
| 三、解答题 | |||
| 17 | 0.85 | 求二次函数的值域或最值 由对数(型)的单调性求参数 | 问答题 |
| 18 | 0.94 | 求函数值 定义法判断或证明函数的单调性 | 问答题 |
| 19 | 0.65 | 函数奇偶性的定义与判断 求二次函数的值域或最值 求二次函数的解析式 | 证明题 |
| 20 | 0.65 | 由奇偶性求函数解析式 画出具体函数图象 求二次函数的解析式 根据图像判断函数单调性 | 作图题 |
| 21 | 0.65 | 利用函数单调性求最值或值域 利用二次函数模型解决实际问题 指数函数模型的应用(2) | 应用题 |

 的定义域为
的定义域为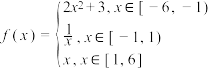 ,则
,则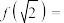
 有五个解,则这五个解之和为
有五个解,则这五个解之和为 ,值域为
,值域为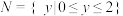 ,则函数
,则函数