1 . 巴普士(约公元3~4世纪),古希腊亚历山大学派著名几何学家.生前有大量的著作,但大部分遗失在历史长河中,仅有《数学汇编》保存下来.《数学汇编》一共8卷,在《数学汇编》第3卷中记载着这样一个定理:“如果在同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于该闭合图形的面积与该闭合图形的重心旋转所得周长的积”, (
( 表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中,
表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中,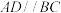 ,
, ,
, ,利用上述定理可求得梯形ABCD的重心G到点B的距离为( )
,利用上述定理可求得梯形ABCD的重心G到点B的距离为( )
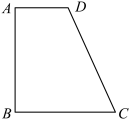
 (
( 表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中,
表示平面闭合图形绕旋转轴旋转所得几何体的体积,S表示闭合图形的面积,l表示重心绕旋转轴旋转一周的周长).已知在梯形ABCD中,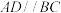 ,
, ,
, ,利用上述定理可求得梯形ABCD的重心G到点B的距离为( )
,利用上述定理可求得梯形ABCD的重心G到点B的距离为( )
A. | B.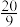 | C.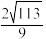 | D.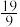 |
您最近一年使用:0次
2023-04-15更新
|
1101次组卷
|
8卷引用:江西省抚州市金溪县第一中学2023届高三下学期4月考试数学(理)试题
江西省抚州市金溪县第一中学2023届高三下学期4月考试数学(理)试题江西省抚州市金溪县第一中学2023届高三下学期4月考试数学(文)试题陕西省榆林市绥德中学2023届高三下学期4月月考文科数学试题九师联盟2023届高三下学期4月联考理科数学试题(老教材)安徽省(九师联盟)2023届二模数学试卷山西省运城市2023届高三二模数学试题(A卷)(已下线)押新高考第5题 数学新文化(已下线)安徽省(九师联盟)2023届二模数学试题变式题6-10
解题方法
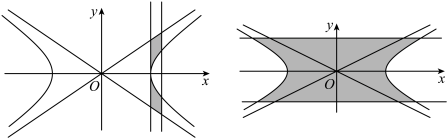
2 . 祖暅原理也称祖氏原理,是一个涉及求几何体体积的著名数学命题,公元656年,唐代李淳风注《九章算术》时提到祖暅的开立圆术,祖暅在求球体积时,使用一个原理,“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.意思是两个同高的几何体,如在等高处的截面面积相等,则体积相等,更详细点说就是,夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积相等,那么这两个几何体的体积相等,上述原理在中国被称为祖暅原理,国外同一般称之为卡瓦列利原理,已知将双曲线 :
: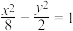 与它的渐近线以及直线
与它的渐近线以及直线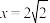 ,
, 围成的图形绕
围成的图形绕 轴旋转一周得到一个旋转体I,将双曲线
轴旋转一周得到一个旋转体I,将双曲线 与直线
与直线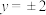 围成的图形绕
围成的图形绕 轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
 :
: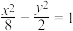 与它的渐近线以及直线
与它的渐近线以及直线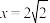 ,
, 围成的图形绕
围成的图形绕 轴旋转一周得到一个旋转体I,将双曲线
轴旋转一周得到一个旋转体I,将双曲线 与直线
与直线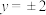 围成的图形绕
围成的图形绕 轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
A.由垂直于 轴的平面截旋转体II,得到的截面为圆面 轴的平面截旋转体II,得到的截面为圆面 |
B.旋转体II的体积为 |
C.将旋转体I放入球中,则球的表面积的最小值为 |
D.旋转体I的体积为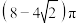 |
您最近一年使用:0次
名校
3 . 古希腊亚历山大时期的数学家帕普斯在《数学汇编》第3卷中记载着一个确定重心的定理:“如果同一平面内的一个闭合图形的内部与一条直线不相交,那么该闭合图形围绕这条直线旋转一周所得到的旋转体的体积等于闭合图形面积乘以该闭合图形的重心旋转所得周长的积”,即 (
( 表示平面图形绕旋转轴旋转的体积,
表示平面图形绕旋转轴旋转的体积, 表示平面图形的面积,
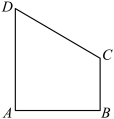
表示平面图形的面积, 表示重心绕旋转轴旋转一周的周长).如图直角梯形
表示重心绕旋转轴旋转一周的周长).如图直角梯形 ,已知
,已知 ,则重心
,则重心 到
到 的距离为( )
的距离为( )
 (
( 表示平面图形绕旋转轴旋转的体积,
表示平面图形绕旋转轴旋转的体积, 表示平面图形的面积,
表示平面图形的面积, 表示重心绕旋转轴旋转一周的周长).如图直角梯形
表示重心绕旋转轴旋转一周的周长).如图直角梯形 ,已知
,已知 ,则重心
,则重心 到
到 的距离为( )
的距离为( )
A.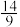 | B.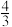 | C.3 | D.2 |
您最近一年使用:0次
2023-01-12更新
|
1012次组卷
|
5卷引用:广东省华附、省实、广雅、深中2023届高三上学期四校联考数学试题
解题方法
4 . 祖暅原理也称祖氏原理,是一个涉及求几何体体积的著名数学命题.公元656年,唐代李淳风注《九章算术》时提到祖暅的开立圆术,祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高,意思是在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积相等,那么这两个几何体的体积相等,上述原理在中国被称为祖暅原理,国外则一般称之为卡瓦列利原理,已知将双曲线 与它的渐近线以及直线
与它的渐近线以及直线 围成的图形绕x轴旋转一周得到一个旋转体I,将双曲线C与直线
围成的图形绕x轴旋转一周得到一个旋转体I,将双曲线C与直线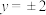 围成的图形绕y轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
围成的图形绕y轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )

①由垂直于y轴的平面截旋转体II,得到的截面为圆面
②旋转体II的体积为
③将旋转体I放入球中,则球的表面积的最小值为
④旋转体I的体积为
 与它的渐近线以及直线
与它的渐近线以及直线 围成的图形绕x轴旋转一周得到一个旋转体I,将双曲线C与直线
围成的图形绕x轴旋转一周得到一个旋转体I,将双曲线C与直线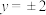 围成的图形绕y轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
围成的图形绕y轴旋转一周得到一个旋转体II,则关于这两个旋转体叙述正确的是( )
①由垂直于y轴的平面截旋转体II,得到的截面为圆面
②旋转体II的体积为

③将旋转体I放入球中,则球的表面积的最小值为

④旋转体I的体积为

| A.①② | B.③④ | C.①③④ | D.①②③ |
您最近一年使用:0次
解题方法
5 . 祖暅原理也称祖氏原理,是我国数学家祖暅提出的一个求积的著名命题:“幂势既同,则积不容异”,“幂”是截面积,“势”是几何体的高,意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.由曲线 ,
, ,
, ,
, 围成的图形绕y轴旋转一周所得旋转体的体积为
围成的图形绕y轴旋转一周所得旋转体的体积为 ,满足
,满足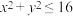 ,
,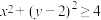 ,
, 的点
的点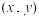 组成的图形绕y轴旋转一周所得旋转体的体积为
组成的图形绕y轴旋转一周所得旋转体的体积为 ,则
,则 、
、 满足的关系式为( )
满足的关系式为( )
 ,
, ,
, ,
, 围成的图形绕y轴旋转一周所得旋转体的体积为
围成的图形绕y轴旋转一周所得旋转体的体积为 ,满足
,满足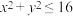 ,
,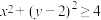 ,
, 的点
的点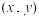 组成的图形绕y轴旋转一周所得旋转体的体积为
组成的图形绕y轴旋转一周所得旋转体的体积为 ,则
,则 、
、 满足的关系式为( )
满足的关系式为( )A.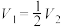 | B. | C.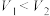 | D. |
您最近一年使用:0次
名校
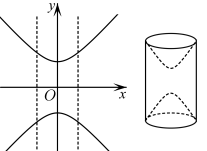
6 . 公元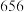 年,唐代李淳风注《九章》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”,意思是两个同高的立体,如在等高处的截面积恒相等,则体积相等.上述原理在中国被称为祖暅原理,我们可以应用此原理将一些复杂几何体转化为常见几何体的组合体来计算体积.如图,将双曲线
年,唐代李淳风注《九章》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”,意思是两个同高的立体,如在等高处的截面积恒相等,则体积相等.上述原理在中国被称为祖暅原理,我们可以应用此原理将一些复杂几何体转化为常见几何体的组合体来计算体积.如图,将双曲线 与直线
与直线 所围成的平面图形绕双曲线的实轴所在直线旋转一周得到几何体
所围成的平面图形绕双曲线的实轴所在直线旋转一周得到几何体 ,下列平面图形绕其对称轴(虚线所示)旋转一周所得几何体与
,下列平面图形绕其对称轴(虚线所示)旋转一周所得几何体与 的体积相同的是( )
的体积相同的是( )

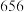 年,唐代李淳风注《九章》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”,意思是两个同高的立体,如在等高处的截面积恒相等,则体积相等.上述原理在中国被称为祖暅原理,我们可以应用此原理将一些复杂几何体转化为常见几何体的组合体来计算体积.如图,将双曲线
年,唐代李淳风注《九章》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”,意思是两个同高的立体,如在等高处的截面积恒相等,则体积相等.上述原理在中国被称为祖暅原理,我们可以应用此原理将一些复杂几何体转化为常见几何体的组合体来计算体积.如图,将双曲线 与直线
与直线 所围成的平面图形绕双曲线的实轴所在直线旋转一周得到几何体
所围成的平面图形绕双曲线的实轴所在直线旋转一周得到几何体 ,下列平面图形绕其对称轴(虚线所示)旋转一周所得几何体与
,下列平面图形绕其对称轴(虚线所示)旋转一周所得几何体与 的体积相同的是( )
的体积相同的是( )

A.图①,长为 、宽为 、宽为 的矩形的两端去掉两个弦长为 的矩形的两端去掉两个弦长为 、半径为 、半径为 的弓形 的弓形 |
B.图②,长为 、宽为 、宽为 的矩形的两端补上两个弦长为 的矩形的两端补上两个弦长为 、半径为 、半径为 的弓形 的弓形 |
C.图③,长为 、宽为 、宽为 的矩形的两端去掉两个底边长为 的矩形的两端去掉两个底边长为 、腰长为 、腰长为 的等腰三角形 的等腰三角形 |
D.图④,长为 、宽为 、宽为 的矩形的两端补上两个底边长为 的矩形的两端补上两个底边长为 、腰长为 、腰长为 的等腰三角形 的等腰三角形 |
您最近一年使用:0次
2022-09-23更新
|
1093次组卷
|
4卷引用:重庆市南开中学校2023届高三上学期9月月考数学试题
重庆市南开中学校2023届高三上学期9月月考数学试题(已下线)第01讲 空间几何体的结构、三视图和直观图与空间几何体的表面积和体积(练)辽宁省沈阳市浑南区东北育才学校科学高中部2023-2024学年高三上学期高考适应性测试(一)数学试题(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点1 祖暅原理及球体积辅助体【培优版】
7 . 祖暅是我国南北朝时期伟大的数学家,他于5世纪末提出了“幂势既同,则积不容异”的体积计算原理,即“夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等”.现已知直线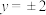 与双曲线
与双曲线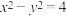 及其渐近线围成的平面图形
及其渐近线围成的平面图形 如图所示.若将图形
如图所示.若将图形 被直线
被直线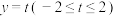 所截得的两条线段绕
所截得的两条线段绕 轴旋转一周,则形成的旋转面的面积
轴旋转一周,则形成的旋转面的面积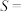
______ ;若将图形 绕
绕 轴旋转一周,则形成的旋转体的体积
轴旋转一周,则形成的旋转体的体积
______ .

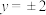 与双曲线
与双曲线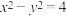 及其渐近线围成的平面图形
及其渐近线围成的平面图形 如图所示.若将图形
如图所示.若将图形 被直线
被直线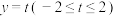 所截得的两条线段绕
所截得的两条线段绕 轴旋转一周,则形成的旋转面的面积
轴旋转一周,则形成的旋转面的面积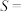
 绕
绕 轴旋转一周,则形成的旋转体的体积
轴旋转一周,则形成的旋转体的体积

您最近一年使用:0次
2022-09-03更新
|
702次组卷
|
3卷引用:湖北省武汉市第十九中学2023届高三上学期11月线上月考数学试题
8 . 祖暅(公元5-6世纪),祖冲之之子,是我国齐梁时代的数学家.他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为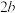 ,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面
,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面 上.以平行于平面
上.以平行于平面 的平面于距平面
的平面于距平面 任意高d处可横截得到
任意高d处可横截得到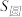 及
及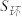 两截面,可以证明
两截面,可以证明 总成立.据此,短轴长为
总成立.据此,短轴长为 ,长轴为
,长轴为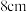 的椭球体的体积是( )
的椭球体的体积是( )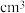
 ,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面
,高皆为a的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面 上.以平行于平面
上.以平行于平面 的平面于距平面
的平面于距平面 任意高d处可横截得到
任意高d处可横截得到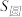 及
及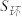 两截面,可以证明
两截面,可以证明 总成立.据此,短轴长为
总成立.据此,短轴长为 ,长轴为
,长轴为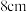 的椭球体的体积是( )
的椭球体的体积是( )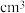

A. | B. | C. | D.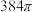 |
您最近一年使用:0次
2021-07-09更新
|
215次组卷
|
4卷引用:江苏省镇江市2020-2021学年高二上学期12月校际联考数学试题
9 . 我国古代数学家祖暅求几何体的体积时,提出一个原理:幂势即同,则积不容异.意思是:夹在两个平行平面之间的两个等高的几何体被平行于这两个面的平面去截,若截面积相等,则两个几何体的体积相等,这个定理的推广是:夹在两个平行平面间的几何体,被平行于这两个平面的平面所截,若截得两个截面面积比为 ,则两个几何体的体积比也为
,则两个几何体的体积比也为 .已知线段
.已知线段 长为4,直线
长为4,直线 过点
过点 且与
且与 垂直,以
垂直,以 为圆心,以1为半径的圆绕
为圆心,以1为半径的圆绕 旋转一周,得到环体
旋转一周,得到环体 ;以
;以 ,
, 分别为上下底面的圆心,以1为上下底面半径的圆柱体
分别为上下底面的圆心,以1为上下底面半径的圆柱体 ;过
;过 且与
且与 垂直的平面为
垂直的平面为 ,平面
,平面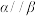 ,且距离为
,且距离为 ,若平面
,若平面 截圆柱体
截圆柱体 所得截面面积为
所得截面面积为 ,平面
,平面 截环体
截环体 所得截面面积为
所得截面面积为 ,则
,则
________ ,环体 体积为
体积为_________ .

 ,则两个几何体的体积比也为
,则两个几何体的体积比也为 .已知线段
.已知线段 长为4,直线
长为4,直线 过点
过点 且与
且与 垂直,以
垂直,以 为圆心,以1为半径的圆绕
为圆心,以1为半径的圆绕 旋转一周,得到环体
旋转一周,得到环体 ;以
;以 ,
, 分别为上下底面的圆心,以1为上下底面半径的圆柱体
分别为上下底面的圆心,以1为上下底面半径的圆柱体 ;过
;过 且与
且与 垂直的平面为
垂直的平面为 ,平面
,平面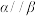 ,且距离为
,且距离为 ,若平面
,若平面 截圆柱体
截圆柱体 所得截面面积为
所得截面面积为 ,平面
,平面 截环体
截环体 所得截面面积为
所得截面面积为 ,则
,则
 体积为
体积为
您最近一年使用:0次
2020-12-14更新
|
572次组卷
|
8卷引用:安徽省池州市东至县2020-2021学年高三上学期12月大联考数学(文)试题
安徽省池州市东至县2020-2021学年高三上学期12月大联考数学(文)试题安徽省池州市东至县2020-2021学年高三上学期12月大联考数学(理)试题安徽省全省名校实验班2020-2021学年高三上学期大联考文科数学试题(已下线)专题16 空间几何体(客观题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题15 空间几何体(客观题)-2021年高考数学(文)二轮复习热点题型精选精练(已下线)专题15 空间几何体(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)江苏省2021届高三高考数学全真模拟试题(一)(已下线)专题22 祖暅原理
10 . 我国南北朝时期的著名数学家祖暅原提出了祖暅原理:“幂势既同,则积不容异.”意思是,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等,即 .现将椭圆
.现将椭圆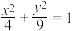 绕
绕 轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
 .现将椭圆
.现将椭圆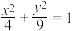 绕
绕 轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
A. | B. | C. | D. |
您最近一年使用:0次
2020-12-02更新
|
3654次组卷
|
13卷引用:山东省潍坊第四中学2022届高三上学期第一次过程检测数学试题
山东省潍坊第四中学2022届高三上学期第一次过程检测数学试题上海市嘉定区育才中学2024届高三上学期12月月考数学试题浙江省宁波市北仑中学2020-2021学年高二上学期期中数学试题辽宁省沈阳市二十中学2022-2023学年高三上学期三模考试数学试题(已下线)专题07 立体几何小题常考全归类(精讲精练)-2吉林省长春市第二实验中学2022-2023学年高三上学期期末数学试题山西省山西大学附属中学校2022-2023学年高二上学期11月期中考试数学试题四川省南充高级中学2023届高考模拟检测七文科数学试题四川省南充高级中学2023届高考模拟检测(七)理科数学试题重庆市2023届高三上学期期中数学试题(已下线)立体几何新定义(已下线)压轴题立体几何新定义题(九省联考第19题模式)练上海市杨浦高级中学2023-2024学年高二下学期期中考试数学试卷



