解题方法
1 . 针对时下的“抖音热”,校团委对“学生性别和喜欢抖音是否有关”作了调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的 ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数 ,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
附表:
附:
 ,女生喜欢抖音的人数占女生人数
,女生喜欢抖音的人数占女生人数 ,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人
,若有90%的把握认为是否喜欢抖音和性别有关,则调查人数中男生可能有( )人附表:
 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |

| A.20 | B.30 | C.35 | D.40 |
您最近一年使用:0次
2023-12-21更新
|
580次组卷
|
4卷引用:8.3.2独立性检验练习
8.3.2独立性检验练习辽宁省鞍山市第六中学2024届高三下学期第二次质量检测数学试题卷(已下线)第四章 统计 专题三 独立性检验 微点2 独立性检验(二)【培优版】福建省漳州市东山第二中学2021-2022学年高二下学期期中考试数学(A)试题
名校
2 . 下列说法正确的有( )
A.随机变量 的方差 的方差 越大,则随机变量 越大,则随机变量 的取值与均值 的取值与均值 的偏离程度越大 的偏离程度越大 |
B.随机抛掷质地均匀的硬币100次,出现50次正面向上的可能性为 |
C.根据分类变量 与 与 的样本数据计算得到 的样本数据计算得到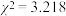 ,根据小概率 ,根据小概率 的独立性检验( 的独立性检验( ),可判断 ),可判断 与 与 有关,且犯错误的概率不超过0.05 有关,且犯错误的概率不超过0.05 |
D.若变量 关于变量 关于变量 的经验回归方程为 的经验回归方程为 时,则变量 时,则变量 与 与 负相关 负相关 |
您最近一年使用:0次
2023-07-25更新
|
314次组卷
|
4卷引用:8.3.2 独立性检验(分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)
(已下线)8.3.2 独立性检验(分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)高二下学期期末数学试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)海南省琼海市嘉积中学2023-2024学年高二下学期期中考试数学试题(A卷)安徽省芜湖市2022-2023学年高二下学期教学质量统测数学试题
解题方法
3 . 下列说法中正确的是( )
本题可参考独立性检验临界值表:
本题可参考独立性检验临界值表:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
A.在线性回归模型中, 越接近于1,表示回归效果越好 越接近于1,表示回归效果越好 |
B.在回归直线方程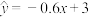 中,当变量 中,当变量 每减少一个单位时,变量 每减少一个单位时,变量 增加0.6个单位 增加0.6个单位 |
C.在一个 列联表中,由计算得 列联表中,由计算得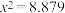 .则认为这两个变量有关系犯错误的概率不超过0.01 .则认为这两个变量有关系犯错误的概率不超过0.01 |
D.已知随机变量 服从正态分布 服从正态分布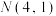 ,且 ,且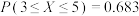 ,则 ,则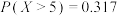 |
您最近一年使用:0次
名校
4 . 下列说法正确的是( )
A.若事件 相互独立,则 相互独立,则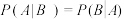 |
B.设随机变量 满足 满足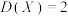 ,则 ,则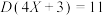 |
C.已知随机变量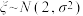 ,且 ,且 ,则 ,则 |
D.在一个 列联表中,计算得到 列联表中,计算得到 的值越接近1,则两个变量的相关性越强 的值越接近1,则两个变量的相关性越强 |
您最近一年使用:0次
2023-07-09更新
|
472次组卷
|
2卷引用:天津市第七中学2024届高三三模数学试题
解题方法
5 . 某校高二年级羽毛球社团为了解喜欢羽毛球运动是否与性别有关,随机在高二年级抽取了若干人进行调查.已知抽取的女生人数是男生人数的3倍,其中女生喜爱羽毛球运动的人数占女生人数的 ,男生喜爱羽毛球运动的人数占男生人数的
,男生喜爱羽毛球运动的人数占男生人数的 .若本次调查得出“在犯错误的概率不超过0.05的前提下,认为喜爱羽毛球运动与性别有关”的结论,则被调查的男生至少有( )
.若本次调查得出“在犯错误的概率不超过0.05的前提下,认为喜爱羽毛球运动与性别有关”的结论,则被调查的男生至少有( )
参考公式及数据: .
.
 ,男生喜爱羽毛球运动的人数占男生人数的
,男生喜爱羽毛球运动的人数占男生人数的 .若本次调查得出“在犯错误的概率不超过0.05的前提下,认为喜爱羽毛球运动与性别有关”的结论,则被调查的男生至少有( )
.若本次调查得出“在犯错误的概率不超过0.05的前提下,认为喜爱羽毛球运动与性别有关”的结论,则被调查的男生至少有( )参考公式及数据:
 .
. | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
| A.35人 | B.32人 | C.31人 | D.30人 |
您最近一年使用:0次
2023-07-06更新
|
543次组卷
|
5卷引用:第八章 成对数据的统计分析(单元重点综合测试)(19题新结构)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)
(已下线)第八章 成对数据的统计分析(单元重点综合测试)(19题新结构)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)第06讲 第八章 成对数据的统计分析 章节验收测评卷-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)9.2 独立性检验(五大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第四章 统计 专题三 独立性检验 微点4 独立性检验综合训练【培优版】广东省广州市天河区2022-2023学年高二下学期期末数学试题
名校
6 .  年
年 月
月 日,文化和旅游部公布
日,文化和旅游部公布 年“五一”假期文化和旅游市场情况,全国国内旅游出游合计
年“五一”假期文化和旅游市场情况,全国国内旅游出游合计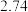 亿人次,同比增长
亿人次,同比增长 某市为了解游客对本地某旅游景区的总体满意度,随机抽取了该景区
某市为了解游客对本地某旅游景区的总体满意度,随机抽取了该景区 名游客进行调查.
名游客进行调查.
(1)请完成 列联表,依据小概率值
列联表,依据小概率值 的独立性检验,能否认为“是否满意”与“游客来源地”有关联?
的独立性检验,能否认为“是否满意”与“游客来源地”有关联?
(2)若将频率视为概率,设随机抽取的 位游客中来自外省且对该景区满意的人数为随机变量
位游客中来自外省且对该景区满意的人数为随机变量 ,求
,求 的数学期望;
的数学期望;
(3)市政府使用综合满意率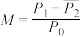 (其中
(其中 表示外省游客满意率,
表示外省游客满意率, 本省游客满意率,
本省游客满意率, 表示整体满意率)来认定星级景区,综合满意率
表示整体满意率)来认定星级景区,综合满意率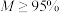 可认定为五星级景区,综合满意率
可认定为五星级景区,综合满意率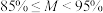 可认定为四星级景区,综合满意率
可认定为四星级景区,综合满意率 为三星级景区,综合满意率
为三星级景区,综合满意率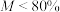 为不定星级景区,请利用样本数据,判断该景区属于什么级别景区.
为不定星级景区,请利用样本数据,判断该景区属于什么级别景区.
附: ,其中
,其中 .
.
 年
年 月
月 日,文化和旅游部公布
日,文化和旅游部公布 年“五一”假期文化和旅游市场情况,全国国内旅游出游合计
年“五一”假期文化和旅游市场情况,全国国内旅游出游合计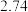 亿人次,同比增长
亿人次,同比增长 某市为了解游客对本地某旅游景区的总体满意度,随机抽取了该景区
某市为了解游客对本地某旅游景区的总体满意度,随机抽取了该景区 名游客进行调查.
名游客进行调查.| 满意 | 不满意 | 合计 | |
| 本省 |  | ||
| 外省 | 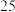 |  | |
| 合计 |
 列联表,依据小概率值
列联表,依据小概率值 的独立性检验,能否认为“是否满意”与“游客来源地”有关联?
的独立性检验,能否认为“是否满意”与“游客来源地”有关联?(2)若将频率视为概率,设随机抽取的
 位游客中来自外省且对该景区满意的人数为随机变量
位游客中来自外省且对该景区满意的人数为随机变量 ,求
,求 的数学期望;
的数学期望;(3)市政府使用综合满意率
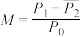 (其中
(其中 表示外省游客满意率,
表示外省游客满意率, 本省游客满意率,
本省游客满意率, 表示整体满意率)来认定星级景区,综合满意率
表示整体满意率)来认定星级景区,综合满意率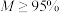 可认定为五星级景区,综合满意率
可认定为五星级景区,综合满意率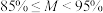 可认定为四星级景区,综合满意率
可认定为四星级景区,综合满意率 为三星级景区,综合满意率
为三星级景区,综合满意率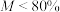 为不定星级景区,请利用样本数据,判断该景区属于什么级别景区.
为不定星级景区,请利用样本数据,判断该景区属于什么级别景区. |  |  |  |  |  |
 |  |  |  |  |  |
 ,其中
,其中 .
.| 满意 | 不满意 | 合计 | |
| 本省 |  |  |  |
| 外省 |  | 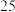 |  |
| 合计 |  | 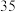 |  |
您最近一年使用:0次
2023-07-05更新
|
191次组卷
|
3卷引用:湖南省常德市汉寿县第一中学2024届高三下学期开学考试数学试题
名校
7 . 某校“足球社团”调查学生喜欢足球是否与性别有关,现从全校学生中随机抽取了
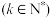 人,若被抽查的男生与女生人数之比为5:3,男生中喜欢足球的人数占男生的
人,若被抽查的男生与女生人数之比为5:3,男生中喜欢足球的人数占男生的 ,女生中喜欢足球的人数占女生的
,女生中喜欢足球的人数占女生的 .经计算,有95%的把握认为喜欢足球与性别有关,但没有99%的把握认为喜欢足球与性别有关.
.经计算,有95%的把握认为喜欢足球与性别有关,但没有99%的把握认为喜欢足球与性别有关.
(1)请完成下面的列联表,并求出k的值;
(2)将频率视为概率,用样本估计总体,从全校男学生中随机抽取4人,记其中喜欢足球的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中 .
.

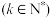 人,若被抽查的男生与女生人数之比为5:3,男生中喜欢足球的人数占男生的
人,若被抽查的男生与女生人数之比为5:3,男生中喜欢足球的人数占男生的 ,女生中喜欢足球的人数占女生的
,女生中喜欢足球的人数占女生的 .经计算,有95%的把握认为喜欢足球与性别有关,但没有99%的把握认为喜欢足球与性别有关.
.经计算,有95%的把握认为喜欢足球与性别有关,但没有99%的把握认为喜欢足球与性别有关.(1)请完成下面的列联表,并求出k的值;
| 喜欢足球 | 不喜欢足球 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.附:
 ,其中
,其中 .
.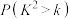 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |
您最近一年使用:0次
2023-07-04更新
|
167次组卷
|
2卷引用:辽宁省沈文新高考研究联盟2025届高三上学期期中质量监测数学试题
名校
解题方法
8 . 下列命题为真命题的有( )
A.若随机变量 的方差为 的方差为 ,则 ,则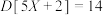 . . |
B.已知经验回归方程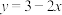 ,则 ,则 与 与 具有正线性相关关系. 具有正线性相关关系. |
C.对于随机事件 与 与 ,若 ,若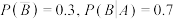 则事件 则事件 与 与 独立. 独立. |
D.根据分类变量 与 与 的成对样本数据,计算得到 的成对样本数据,计算得到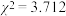 ,根据 ,根据 的独立性检验 的独立性检验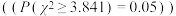 ,有 ,有 的把握认为 的把握认为 与 与 有关. 有关. |
您最近一年使用:0次
2023-06-28更新
|
1216次组卷
|
5卷引用:天津市滨海新区塘沽第一中学等十二校2023-2024学年高三下学期二模考前模拟考试数学试卷
名校
解题方法
9 . 在“双减”政策背景之下,某校就推进学校、家庭、社会体育教育的“一体化”,实现“教会、勤练、常赛”的核心任务.学校组织人员对在校学生“是否喜爱运动”做了一次随机调查.共随机调查了18名男生和12名女生,调查发现,男、女生中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下 列联表:
列联表:
能否有90%把握认为性别与喜爱运动有关?
(2)从被调查的女生中抽取3人,若其中喜爱运动的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(附参考公式及参考数据): ,其中
,其中 .
.
(1)根据以上数据完成以下
 列联表:
列联表:| 喜欢运动 | 不喜欢运动 | 总计 | ||
| 男 | ||||
| 女 | ||||
| 总计 | ||||
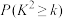 | 0.15 | 0.10 | 0.05 | 0.025 |
 | 2.072 | 2.706 | 3.841 | 5.024 |
(2)从被调查的女生中抽取3人,若其中喜爱运动的人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.(附参考公式及参考数据):
 ,其中
,其中 .
.
您最近一年使用:0次
2023-10-25更新
|
587次组卷
|
3卷引用:第02讲 成对数据的统计分析(五大题型)(讲义)
解题方法
10 . 为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本校学生体育锻的经常性有影响,随机抽取了300名学生,对他们是否经常锻炼的情况进行了调查,调查发现经常锻炼人数是不经常锻炼人数的2倍,绘制其等高堆积条形图,如图所示,则( )


| A.参与调查的男生中经常锻炼的人数比不经常锻炼的人数多 | ||||||||||||
B.从参与调查的学生中任取一人,已知该生为女生,则该生经常锻炼的概率为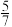 | ||||||||||||
C.依据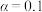 的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.1 的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.1 | ||||||||||||
D.假设调查人数为600人,经常锻炼人数与不经常锻炼人数的比例不变,统计得到的等高堆积条形图也不变,依据 的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.05 的独立性检验,认为性别因素影响学生体育锻炼的经常性,该推断犯错误的概率不超过0.05附:  , ,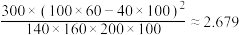
|
您最近一年使用:0次



