1 . 对于在区间 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的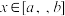 ,均有
,均有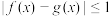 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.
(1)若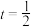 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合 ;
;
(3)在(2)的条件下,是否存在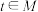 ,使得
,使得 与
与 在给定区间
在给定区间 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 上有意义的两个函数
上有意义的两个函数 与
与 ,如果对任意的
,如果对任意的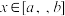 ,均有
,均有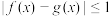 ,则称
,则称 与
与 在
在 上是接近的,否则称
上是接近的,否则称 与
与 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间 .
.(1)若
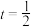 ,判断
,判断 与
与 是否在给定区间上接近;
是否在给定区间上接近;(2)若
 与
与 在给定区间
在给定区间 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合 ;
;
(3)在(2)的条件下,是否存在
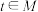 ,使得
,使得 与
与 在给定区间
在给定区间 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,解不等式
时,解不等式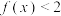 的解集;
的解集;
(2)当 时,写出函数
时,写出函数 的单调区间;
的单调区间;
(3)若在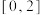 上存在
上存在 个不同的实数
个不同的实数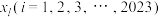 ,
, ,使得
,使得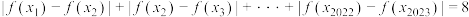 ,求实数
,求实数 的取值范围.
的取值范围.
 ,其中
,其中 为常数.
为常数.(1)当
 时,解不等式
时,解不等式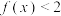 的解集;
的解集;(2)当
 时,写出函数
时,写出函数 的单调区间;
的单调区间;(3)若在
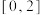 上存在
上存在 个不同的实数
个不同的实数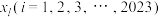 ,
, ,使得
,使得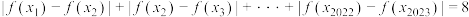 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-17更新
|
434次组卷
|
2卷引用:湖北省十堰市示范高中教联体测评联盟2023-2024学年高一上学期11月联考数学试题
名校
3 . 已知函数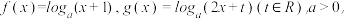 且
且
(1)若方程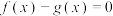 的一个实数根为2,求
的一个实数根为2,求 的值;
的值;
(2)当 且
且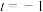 时,求不等式
时,求不等式 的解集;
的解集;
(3)若函数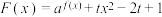 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
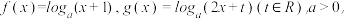 且
且
(1)若方程
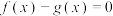 的一个实数根为2,求
的一个实数根为2,求 的值;
的值;(2)当
 且
且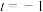 时,求不等式
时,求不等式 的解集;
的解集; (3)若函数
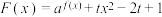 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2019-11-30更新
|
945次组卷
|
6卷引用:湖北省荆州市沙市中学2019-2020学年高一上学期期中数学试题



