名校
1 . 点P在圆 上,点Q在圆
上,点Q在圆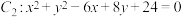 上,则( )
上,则( )
 上,点Q在圆
上,点Q在圆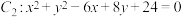 上,则( )
上,则( )A.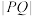 的最小值为0 的最小值为0 |
B.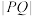 的最大值为7 的最大值为7 |
C.两个圆心所在直线的斜率为 |
D.两个圆的公共弦所在直线的方程为 |
您最近一年使用:0次
7日内更新
|
1057次组卷
|
35卷引用:山东省聊城市2020-2021学年第一学期高二期中考试数学试题
山东省聊城市2020-2021学年第一学期高二期中考试数学试题山东省泰安市肥城市2020-2021学年高二上学期期末数学试题山东省泰安市宁阳县第一中学2020-2021学年高二上学期期末数学试题山东省泰安市2020-2021学年高二上学期期末数学试题广东省汕头市达濠华侨中学2020-2021学年高二上学期期末联考数学试题北师大版(2019) 选修第一册 必杀技 第一章 素养检测(已下线)卷11 选择性必修第一册高二上期中考试 总复习检测2(易)-2021-2022学年高二数学单元卷模拟(易中难)(2019人教A版选择性必修第一册+第二册)苏教版(2019) 选修第一册 必杀技 第二章 素养检测(已下线)“8+4+4”小题强化训练(45)直线与圆的综合应用-2022届高考数学一轮复习(江苏等新高考地区专用)(已下线)第2章 直线和圆的方程 章末测试(基础)-2021-2022学年高二数学一隅三反系列(人教A版2019选择性必修第一册)湖北省襄阳市枣阳一中2021-2022学年高二上学期10月月考数学试题广东省广州市仲元中学2021-2022学年高二上学期期中数学试题广东省广州市八十九中2021-2022学年高二上学期期中数学试题广东省广州市第八十九中学2021-2022学年高一上学期期中数学试题福建省福州市连江尚德中学等六校2021-2022学年高二上学期期中考数学试题(已下线)专题2.1 圆与方程 章末检测1(易)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)专题2.2 直线和圆的方程 章末检测2(中)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第一册)黑龙江省鸡西实验中学2021-2022学年高二上学期期中考试数学试题江苏省扬州市邵伯高级中学2022-2023学年高二上学期期中数学试题浙江省绍兴市越州中学2022-2023学年高二上学期期中测试(一)数学试题江苏省宿迁市北大附属宿迁实验学校2022-2023学年高二上学期11月期中数学试题安徽省合肥世界外国语学校2022-2023学年高二上学期期末数学试题安徽省滁州市定远县育才学校2022-2023学年高二上学期11月期中考试数学试题第一章 直线与圆 综合培优卷(已下线)高二上学期期中【全真模拟卷01】(人教A版2019)广东省东莞实验中学2022-2023学年高二上学期期中数学试题(已下线)第10讲 圆与圆的位置关系(5大考点)山东省青岛市第十七中学2022-2023学年高二上学期期末数学试题(已下线)期中真题必刷基础60题(47个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)(已下线)期末精确押题之多选题(40题)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)(已下线)高二数学第一学期期期末押题密卷06卷【巩固卷】第2章平面解析几何初步素养检测 单元测试A-湘教版(2019)选择性必修第一册湖南省衡阳市衡阳县部分学校2024-2025学年高二上学期第一次月考数学测评卷(A卷)河南省南阳市内乡县夏关高中2024-2025学年高二上学期第一次阶段性测试数学试题安徽省蚌埠市五河第一中学2024-2025学年高二上学期第二次月考检测数学试题
名校
解题方法
2 . 已知直线 与直线
与直线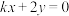 互相垂直,则它们的交点坐标为( )
互相垂直,则它们的交点坐标为( )
 与直线
与直线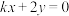 互相垂直,则它们的交点坐标为( )
互相垂直,则它们的交点坐标为( )A. | B.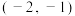 |
C. | D.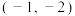 |
您最近一年使用:0次
2024-01-15更新
|
751次组卷
|
14卷引用:重庆市巴蜀中学2020-2021学年高二上学期期中数学试题
重庆市巴蜀中学2020-2021学年高二上学期期中数学试题山东省聊城市2021-2022学年高二上学期期中数学试题(已下线)第10讲 两条直线的交点坐标-【帮课堂】山东省临沂市兰山区、罗庄区2021-2022学年高二上学期中考试数学试题山东省临沂市兰陵县2021-2022学年高二上学期期中数学试题山东省临沂市多县区2021-2022学年高二上学期期中教学质量检测数学试题福建省龙岩第一中学2022-2023学年高二上学期第二次月考数学试题福建省龙岩第一中学2022-2023学年高二(实验班)上学期第二次月考数学试题山东省临沂市临沂第二中学2022-2023学年高二上学期期中数学试题新疆乌鲁木齐市第六十一中学2023-2024学年高二上学期第一次月考数学试题(已下线)第一章 直线与方程(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第一册)(已下线)第12讲 直线的交点坐标与距离公式-【暑假自学课】(人教A版2019选择性必修第一册)(已下线)2.3.1 两条直线的交点坐标——课堂例题(已下线)2.2.3 两条直线的位置关系——课后作业(提升版)
名校
解题方法
3 . 已知两圆 和
和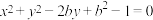 恰有三条公切线,若
恰有三条公切线,若 ,
, ,且
,且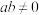 ,则
,则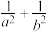 的最小值为( )
的最小值为( )
 和
和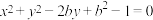 恰有三条公切线,若
恰有三条公切线,若 ,
, ,且
,且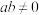 ,则
,则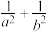 的最小值为( )
的最小值为( )A. | B. | C.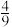 | D.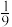 |
您最近一年使用:0次
2024-01-05更新
|
716次组卷
|
11卷引用:【市级联考】山东省聊城市2019届高三三模试卷理科数学试题
【市级联考】山东省聊城市2019届高三三模试卷理科数学试题(已下线)专题7.4 不等式(单元测试)(测)【文】-《2020年高考一轮复习讲练测》(已下线)专题7.4 第七章 不等式 (单元测试)(测)-江苏版《2020年高考一轮复习讲练测》2020届宁夏石嘴山市第三中学高三上学期期中考试数学(理)试题重庆市育才中学2020届高三下学期入学考试数学(理)试题宁夏石嘴山市第三中学2020届高三上学期期中数学(理)试题(已下线)10.2 圆的方程陕西省西安市长安区第一中学2022-2023学年高二上学期期末理科数学试题(已下线)2.5.2 圆与圆的位置关系【第三练】“上好三节课,做好三套题“高中数学素养晋级之路广东省汕头市金山中学2023-2024学年高二上学期期末考试数学试题(已下线)直线与圆、圆与圆的位置关系-一轮复习考点专练
名校
4 . 若直线 的一个方向向量为
的一个方向向量为 ,则它的倾斜角为( )
,则它的倾斜角为( )
 的一个方向向量为
的一个方向向量为 ,则它的倾斜角为( )
,则它的倾斜角为( )A. | B. | C. | D. |
您最近一年使用:0次
2023-02-14更新
|
1782次组卷
|
30卷引用:山东省聊城市2021-2022学年高二上学期期末数学试题
山东省聊城市2021-2022学年高二上学期期末数学试题重庆市青木关中学2020-2021学年高二上学期期中数学试题安徽省蚌埠第三中学2021-2022学年高二上学期10月教学质量检测数学试题广东省佛山市南海区西樵高级中学2021-2022学年高二上学期期中数学试题辽宁省丹东市凤城市第一中学2021-2022学年高二上学期12月月考数学试题广东省揭阳华侨高级中学2021-2022学年高二上学期期中数学试题安徽省六安市新安中学2021-2022学年高二上学期12月月考数学试题辽宁省沈阳市第二中学2022-2023学年高二上学期第一次月考数学试题浙江省嘉兴市桐乡市茅盾中学2022-2023学年高二上学期第一次考试数学试题辽宁省铁岭市昌图县第一高级中学2022-2023学年高二上学期10月月考数学试题天津市静海区第一中学2022-2023学年高二上学期第一次月考数学试题吉林省通白城市榆县第一中学校2022-2023学年高二上学期第二次质量检测数学试题辽宁省鞍山市鞍钢高级中学2022-2023学年高二上学期10月月考数学试题河北省邯郸市魏县第五中学2022-2023学年高二上学期第二次月考数学试题天津市宁河区芦台第一中学2022-2023学年高二上学期第一次学习诊断数学试题广西梧州市藤县第六中学2022-2023学年高二上学期10月月考数学试题浙江省杭州市长河高级中学2022-2023学年高二上学期期末数学试题上海市格致中学2022-2023学年高二下学期期中数学试题(已下线)第12讲 倾斜角与斜率5种常见考法归类-【暑假自学课】2023年新高二数学暑假精品课(人教A版2019选择性必修第一册)广东省东莞市石竹实验学校2023-2024学年高二上学期10月月考数学试题广东省肇庆市第一中学2023-2024学年高二上学期期中数学试题吉林省长春市农安县2023-2024学年高二上学期期中考试数学试题福建省泉州市泉州九中与侨光中学2023-2024学年高二上学期12月联考数学试题天津市第一中学滨海学校2023-2024学年高二上学期第二次月考数学试题(已下线)专题01 直线的倾斜角与斜率-【寒假自学课】2024年高二数学寒假提升学与练(沪教版2020)福建省莆田第一中学2023-2024学年高二下学期期初考试数学试卷(已下线)专题01平面直角坐标系中的直线全章复习攻略--高二期末考点大串讲(沪教版2020选修)(已下线)2.1.1 倾斜角与斜率——课堂例题广东省佛山市顺德区龙江中学2024-2025学年高二上学期10月月考数学试卷广东实验中学附属江门学校2024-2025学年高二上学期10月阶段性测试数学试题B卷
名校
5 . 已知三角形ABC的顶点坐标为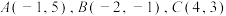 .
.
(1)求过点C且与边AB平行的直线方程;
(2)求AB边上的高所在的直线方程.
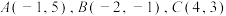 .
.(1)求过点C且与边AB平行的直线方程;
(2)求AB边上的高所在的直线方程.
您最近一年使用:0次
2024-09-03更新
|
2004次组卷
|
5卷引用:湖南省株洲市茶陵县第二中学2015-2016年学年高一下学期期末数学试题
名校
解题方法
6 . 如图,已知长方体 中,
中,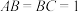 ,
,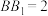 ,连接
,连接 ,过B点作
,过B点作 的垂线交
的垂线交 于E,交
于E,交 于F.
于F.

(1)求证: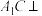 平面
平面 ;
;
(2)求点A到平面 的距离;
的距离;
 中,
中,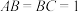 ,
,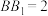 ,连接
,连接 ,过B点作
,过B点作 的垂线交
的垂线交 于E,交
于E,交 于F.
于F.
(1)求证:
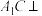 平面
平面 ;
;(2)求点A到平面
 的距离;
的距离;
您最近一年使用:0次
2023-10-19更新
|
766次组卷
|
5卷引用:【全国百强校】河北省遵化市堡子店中学2017-2018学年高二下学期期末考试(文科)数学试题
名校
解题方法
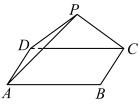
7 . 如图,已知,四边形ABCD为长方形,平面PDC⊥平面ABCD,PD=PC=4,AB=6,BC=3.
(2)证明:求点C到平面PDA的距离.
(2)证明:求点C到平面PDA的距离.
您最近一年使用:0次
2022-12-08更新
|
336次组卷
|
5卷引用:新疆乌鲁木齐市第四中学2019-2020学年高一下学期期末考试数学试题
新疆乌鲁木齐市第四中学2019-2020学年高一下学期期末考试数学试题山东省聊城第一中学2023-2024学年高一下学期第二次阶段性测试数学试题新疆巴音郭楞蒙古自治州第二中学2021届高三上学期开学第一次摸底考试数学(文)试题河南省安阳市第一中学2020-2021学年高一上学期期末数学试题(已下线)8.6.2 空间角与空间距离(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)
名校
解题方法
8 . 已知圆 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)若点 的坐标为
的坐标为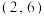 ,求直线
,求直线 的方程;
的方程;
(2)求证:直线 恒过定点
恒过定点 ,并求出该定点
,并求出该定点 的坐标.
的坐标.
 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.(1)若点
 的坐标为
的坐标为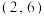 ,求直线
,求直线 的方程;
的方程;(2)求证:直线
 恒过定点
恒过定点 ,并求出该定点
,并求出该定点 的坐标.
的坐标.
您最近一年使用:0次
2022-12-05更新
|
433次组卷
|
3卷引用:山东省聊城市2020-2021学年第一学期高二期中考试数学试题
名校
9 . 已知直线y=k(x+2)与曲线 有两个不同的公共点,则k的取值范围是
有两个不同的公共点,则k的取值范围是 ___ .
 有两个不同的公共点,则k的取值范围是
有两个不同的公共点,则k的取值范围是
您最近一年使用:0次
2021-10-22更新
|
1020次组卷
|
8卷引用:山东省青岛第五十八中学2020-2021学年高二上学期期中考试数学试题
山东省青岛第五十八中学2020-2021学年高二上学期期中考试数学试题山东省聊城颐中外国语学校2023-2024学年高二上学期期中考试数学试题江苏省苏州市星海实验中学2021-2022学年高二上学期10月学情调研数学试题河北省衡水市第十四中学(西校区)2021-2022学年高二上学期二调数学试题山东省青岛市青岛第五十八中学2011-2022学年高二上学期期中数学试题山东省青岛市青岛第二中学分校2022-2023学年高二上学期期中数学试题(已下线)综合测试卷(基础版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)浙江省温岭市新河中学2024-2025学年高二上学期10月阶段性考试数学试题
名校
解题方法
10 . 瑞士数学家欧拉(Euler)1765年在其所著的《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(-4,0),B(0,4),其欧拉线方程为x-y+2=0,则顶点C的坐标可以是( )
| A.(2,0) | B.(0,2) | C.(-2,0) | D.(0,-2) |
您最近一年使用:0次
2021-12-31更新
|
2126次组卷
|
28卷引用:广东省佛山市2019-2020学年高二上学期期末数学试题
广东省佛山市2019-2020学年高二上学期期末数学试题(已下线)专题11 直线与圆-备战2020年新高考数学新题型之【多选题】-《2020年新高考政策解读与配套资源》(已下线)专题18 立体几何(1)-2020年新高考新题型多项选择题专项训练江苏省南通市如东高级中学2019-2020学年高一下学期4月阶段测试数学试题江苏省南通市海安高级中学2019-2020学年高二下学期5月月考数学试题(已下线)数学-6月大数据精选模拟卷03(海南卷)(满分冲刺篇)福建省福州第一中学2019-2020学年高一下学期期末考试数学试题湖北省部分省级示范高中2020-2021学年高二上学期期中联考数学试题福建省厦门第六中学2020-2021学年高二上学期期中考试数学试题江苏省泰州市靖江市斜桥中学2020-2021学年高三上学期12月阶段性检测数学试题山东省聊城市2021-2022学年高二上学期期中数学试题(已下线)专题10 直线和圆的方程(单元测试卷)-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)第一章 直线与方程(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)重庆市万州第二高级中学2021-2022学年高二上学期第一次月考数学试题河北省实验中学2022届高三上学期开学考试数学试题江苏省泰州市第二中学2021-2022学年高二上学期第一次月考数学试题(已下线)数学与数学著作(已下线)专题05 《直线与方程》中的压轴题(1)(原卷版)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)山东省临沂市兰山区、罗庄区2021-2022学年高二上学期中考试数学试题山东省临沂市兰陵县2021-2022学年高二上学期期中数学试题(已下线)专题06 《圆与方程》中的压轴题(2)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)重庆市第八中学校2022届高三下学期高考适应性强化训练(四)数学试题山东省临沂市多县区2021-2022学年高二上学期期中教学质量检测数学试题第1章 直线与方程(培优卷)直线与圆的位置关系山东省临沂市临沂第二中学2022-2023学年高二上学期期中数学试题辽宁省部分学校2022-2023学年高三下学期高考适应性测试数学试题江苏省常州市第一中学2023-2024学年高二上学期11月期中数学试题



