名校
解题方法
1 . 某校对2023年高一上学期期末数学考试成绩(单位:分)进行分析,随机抽取100名学生,将分数按照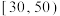 ,
, ,
,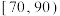 ,
,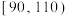 ,
,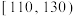 ,
,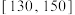 分成6组,绘制成如图所示的频率分布直方图:
分成6组,绘制成如图所示的频率分布直方图: 的值;
的值;
(2)估计该校高一上学期期末数学考试成绩的中位数;
(3)为了进一步了解学生对数学学习的情况,在成绩位于 和
和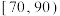 的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在
的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在 内的概率.
内的概率.
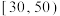 ,
, ,
,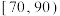 ,
,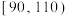 ,
,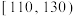 ,
,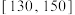 分成6组,绘制成如图所示的频率分布直方图:
分成6组,绘制成如图所示的频率分布直方图: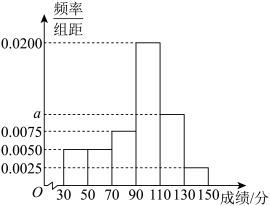
 的值;
的值;(2)估计该校高一上学期期末数学考试成绩的中位数;
(3)为了进一步了解学生对数学学习的情况,在成绩位于
 和
和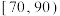 的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在
的两组中,用按比例分配的分层随机抽样的方法抽取5名学生,再从这5名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生至少有1人成绩在 内的概率.
内的概率.
您最近半年使用:0次
2 . 某中学举行了一次“垃圾分类知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩x(单位:分,得分取正整数,满分为100分)作为样本进行统计将成绩进行整理后,分为五组( ,
,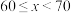 ,
,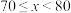 ,
, ,
,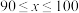 ),其中第4组,第1组,第2组的频数依次成等比数列,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
),其中第4组,第1组,第2组的频数依次成等比数列,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
(2)若根据这次成绩,学校准备淘汰80%的同学,仅留20%的同学进入下一轮竞赛请问晋级分数线划为多少合理?
(3)某老师在此次竞赛成绩中抽取了10名学生的分数: ,
, ,
, ,…,
,…,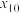 ,已知这10个分数的平均数
,已知这10个分数的平均数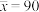 ,标准差
,标准差 ,若剔除其中的95和85两个分数,求剩余8个分数的平均数与方差.(附:方差计算公式:
,若剔除其中的95和85两个分数,求剩余8个分数的平均数与方差.(附:方差计算公式: 或
或
 ,
,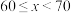 ,
,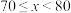 ,
, ,
, ),其中第4组,第1组,第2组的频数依次成等比数列,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
),其中第4组,第1组,第2组的频数依次成等比数列,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题: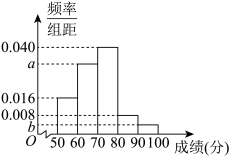
(2)若根据这次成绩,学校准备淘汰80%的同学,仅留20%的同学进入下一轮竞赛请问晋级分数线划为多少合理?
(3)某老师在此次竞赛成绩中抽取了10名学生的分数:
 ,
, ,
, ,…,
,…,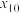 ,已知这10个分数的平均数
,已知这10个分数的平均数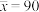 ,标准差
,标准差 ,若剔除其中的95和85两个分数,求剩余8个分数的平均数与方差.(附:方差计算公式:
,若剔除其中的95和85两个分数,求剩余8个分数的平均数与方差.(附:方差计算公式: 或
或
您最近半年使用:0次
3 . 甲乙两人进行投篮比赛,两人各投一次为一轮比赛,约定如下规则:如果在一轮比赛中一人投进,另一人没投进,则投进者得1分,没进者得-1分,如果一轮比赛中两人都投进或都没投进,则都得0分,当两人各自累计总分相差4分时比赛结束,得分高者获胜.在每次投球中甲投进的概率为0.5,乙投进的概率为0.6,每次投球都是相互独立的.
(1)若两人起始分都为0分,求恰好经过4轮比赛,甲获胜的概率.
(2)若规定两人起始分都为2分,记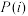 (
(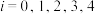 )为甲累计总分为i时,甲最终获胜的概率,则
)为甲累计总分为i时,甲最终获胜的概率,则
①求证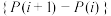 (
( )为等比数列
)为等比数列
②求 的值.
的值.
(1)若两人起始分都为0分,求恰好经过4轮比赛,甲获胜的概率.
(2)若规定两人起始分都为2分,记
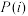 (
(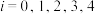 )为甲累计总分为i时,甲最终获胜的概率,则
)为甲累计总分为i时,甲最终获胜的概率,则
①求证
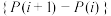 (
( )为等比数列
)为等比数列②求
 的值.
的值.
您最近半年使用:0次
解题方法
4 . 某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的补偿方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如下图所示.
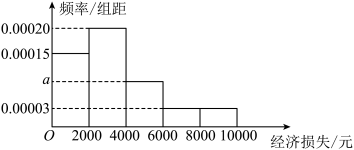
(1)求 的值;
的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在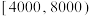 的居民中随机抽取8人,再从这8人中任取2人了解情况,求至多有1人经济损失在
的居民中随机抽取8人,再从这8人中任取2人了解情况,求至多有1人经济损失在 的概率.
的概率.

(1)求
 的值;
的值;(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在
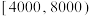 的居民中随机抽取8人,再从这8人中任取2人了解情况,求至多有1人经济损失在
的居民中随机抽取8人,再从这8人中任取2人了解情况,求至多有1人经济损失在 的概率.
的概率.
您最近半年使用:0次
解题方法
5 . 某地足球协会为了调查球迷对第二十二届世界杯的了解情况,组织了一次相关知识测试活动,并从中抽取了50位球迷的测试成绩(取正整数,满分100分)进行统计,按照 ,
, ,
, ,
, ,
, 进行分组并作出频率分布直方图,如图所示.
进行分组并作出频率分布直方图,如图所示.

(1)求a的值,并估计参与本次活动的球迷测试成绩的中位数;
(2)规定测试成绩不低于80分的为“真球迷”,测试成绩不低于90分的为“狂热球迷”,现从该样本中的“真球迷”中随机抽取2人,求抽取的2人中恰有1人为“狂热球迷”的概率.
 ,
, ,
, ,
, ,
, 进行分组并作出频率分布直方图,如图所示.
进行分组并作出频率分布直方图,如图所示.
(1)求a的值,并估计参与本次活动的球迷测试成绩的中位数;
(2)规定测试成绩不低于80分的为“真球迷”,测试成绩不低于90分的为“狂热球迷”,现从该样本中的“真球迷”中随机抽取2人,求抽取的2人中恰有1人为“狂热球迷”的概率.
您最近半年使用:0次
名校
解题方法
6 . 随着中国实施制造强国战略以来,中国制造(Made in china)逐渐成为世界上认知度最高的标签之一,企业也越来越重视产品质量的全程控制某企业从生产的一批产品中抽取40件作为样本,检测其质量指标值,质量指标的范围为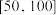 ,经过数据处理后得到如下频率分布直方图.
,经过数据处理后得到如下频率分布直方图.
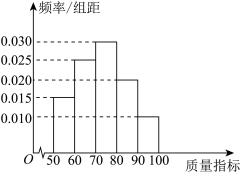
(1)求频率分布直方图中质量指标值的平均数和中位数(结果精确到0.1);
(2)为了进一步检验产品质量,在样本中从质量指标在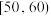 和
和 的两组中抽取2件产品,记至少有一件取自
的两组中抽取2件产品,记至少有一件取自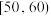 的产品件数为事件A,求事件A的概率.
的产品件数为事件A,求事件A的概率.
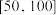 ,经过数据处理后得到如下频率分布直方图.
,经过数据处理后得到如下频率分布直方图.
(1)求频率分布直方图中质量指标值的平均数和中位数(结果精确到0.1);
(2)为了进一步检验产品质量,在样本中从质量指标在
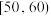 和
和 的两组中抽取2件产品,记至少有一件取自
的两组中抽取2件产品,记至少有一件取自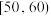 的产品件数为事件A,求事件A的概率.
的产品件数为事件A,求事件A的概率.
您最近半年使用:0次
2023-03-29更新
|
522次组卷
|
2卷引用:广西柳州市2023届高三第三次模拟数学(文)试题
名校
7 . 研究表明,温度的突然变化会引起机体产生呼吸道上皮组织的生理不良反应,从而导致呼吸系统疾病的发生或恶化.某中学数学建模社团成员欲研究昼夜温差大小与该校高三学生患感冒人数多少之间的关系,他们记录了某周连续六天的温差,并到校医务室查阅了这六天中每天高三学生新增患感冒而就诊的人数,得到资料如下:
参考数据: ,
,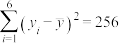 .
.
(1)已知第一天新增患感冒而就诊的学生中有7位女生,从第一天新增的患感冒而就诊的学生中随机抽取3位,若抽取的3人中至少有一位男生的概率为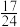 ,求
,求 的值;
的值;
(2)已知两个变量x与y之间的样本相关系数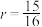 ,请用最小二乘法求出y关于x的经验回归方程
,请用最小二乘法求出y关于x的经验回归方程 ,据此估计昼夜温差为15℃时,该校新增患感冒的学生数(结果保留整数).
,据此估计昼夜温差为15℃时,该校新增患感冒的学生数(结果保留整数).
参考公式: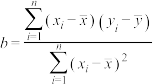 ,
, .
.
| 日期 | 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 |
| 昼夜温差x(℃) | 4 | 7 | 8 | 9 | 14 | 12 |
| 新增就诊人数y(位) |  |  | 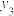 | 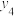 | 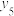 |  |
 ,
,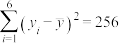 .
.(1)已知第一天新增患感冒而就诊的学生中有7位女生,从第一天新增的患感冒而就诊的学生中随机抽取3位,若抽取的3人中至少有一位男生的概率为
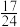 ,求
,求 的值;
的值;(2)已知两个变量x与y之间的样本相关系数
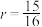 ,请用最小二乘法求出y关于x的经验回归方程
,请用最小二乘法求出y关于x的经验回归方程 ,据此估计昼夜温差为15℃时,该校新增患感冒的学生数(结果保留整数).
,据此估计昼夜温差为15℃时,该校新增患感冒的学生数(结果保留整数).参考公式:
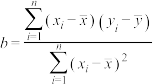 ,
, .
.
您最近半年使用:0次
2023-02-16更新
|
1695次组卷
|
8卷引用:安徽省合肥市2023届高三下学期第一次教学质量检测数学试题
安徽省合肥市2023届高三下学期第一次教学质量检测数学试题(已下线)模块十 计数原理与统计概率-1湖南省长沙市麓山国际实验学校2022-2023学年高三下学期3月自主检测数学试题(已下线)专题18计数原理与概率统计(解答题)(已下线)第8章 成对数据的统计分析(A卷·知识通关练)-【单元测试】2022-2023学年高二数学分层训练AB卷(沪教版2020选择性必修第二册)四川省泸县第四中学2022-2023学年高二下学期3月月考文科数学试题河南省南阳市唐河县第一高级中学2022-2023学年高二下学期2月月考数学试题(已下线)第八章 成对数据的统计分析(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)
名校
8 . 某中学为了解高中一年级学生对《生涯规划》读本学习情况,在该年级 名学生中随机抽取了
名学生中随机抽取了 名学生作为样本,对他们一周内对《生涯规划》读本学习时间进行调查,经统计,这些时间全部介于
名学生作为样本,对他们一周内对《生涯规划》读本学习时间进行调查,经统计,这些时间全部介于 至
至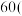 单位
单位 分钟
分钟 之间.现将数据分组,并制成如图所示的频率分布直方图.为了研究的方便,该年级规定,若一周学习《生涯规划》读本时间多于
之间.现将数据分组,并制成如图所示的频率分布直方图.为了研究的方便,该年级规定,若一周学习《生涯规划》读本时间多于 分钟的学生称为“精生涯生”,若一周学习《生涯规划》读本时间小于
分钟的学生称为“精生涯生”,若一周学习《生涯规划》读本时间小于 分钟的学生称为“泛生涯生”.
分钟的学生称为“泛生涯生”.
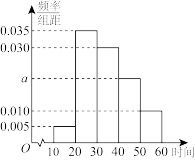
(1)求图中 的值;
的值;
(2)用样本估计总体,估计该年级“精生涯生”和“泛生涯生”的数量各为多少人?
(3)从样本中的“精生涯生”和“泛生涯生”中任选 名学生,求这两名学生一周内对《生涯规划》读本学习时间的差不超过
名学生,求这两名学生一周内对《生涯规划》读本学习时间的差不超过 分钟的概率.
分钟的概率.
 名学生中随机抽取了
名学生中随机抽取了 名学生作为样本,对他们一周内对《生涯规划》读本学习时间进行调查,经统计,这些时间全部介于
名学生作为样本,对他们一周内对《生涯规划》读本学习时间进行调查,经统计,这些时间全部介于 至
至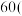 单位
单位 分钟
分钟 之间.现将数据分组,并制成如图所示的频率分布直方图.为了研究的方便,该年级规定,若一周学习《生涯规划》读本时间多于
之间.现将数据分组,并制成如图所示的频率分布直方图.为了研究的方便,该年级规定,若一周学习《生涯规划》读本时间多于 分钟的学生称为“精生涯生”,若一周学习《生涯规划》读本时间小于
分钟的学生称为“精生涯生”,若一周学习《生涯规划》读本时间小于 分钟的学生称为“泛生涯生”.
分钟的学生称为“泛生涯生”.
(1)求图中
 的值;
的值;(2)用样本估计总体,估计该年级“精生涯生”和“泛生涯生”的数量各为多少人?
(3)从样本中的“精生涯生”和“泛生涯生”中任选
 名学生,求这两名学生一周内对《生涯规划》读本学习时间的差不超过
名学生,求这两名学生一周内对《生涯规划》读本学习时间的差不超过 分钟的概率.
分钟的概率.
您最近半年使用:0次
2023-03-16更新
|
525次组卷
|
6卷引用:上海市行知中学2022-2023学年高二上学期期末数学试题
上海市行知中学2022-2023学年高二上学期期末数学试题四川省资阳市2022-2023学年高二上学期期末文科数学试题辽宁省朝阳市建平县实验中学2022-2023学年高一下学期4月月考数学试题(已下线)第13章 统计(常考必刷30题6种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)上海市崇明区横沙中学2023-2024学年高二上学期期末考试数学试题(已下线)专题11统计 (6个知识点10种题型)-【倍速学习法】2023-2024学年高二数学核心知识点与常见题型通关讲解练(沪教版2020必修第三册)
名校
9 . 某新能源汽车制造公司,为鼓励消费者购买其生产的新能源汽车,约定从今年元月开始,凡购买一辆该品牌汽车,在行驶三年后,公司将给予适当金额的购车补贴.某调研机构对已购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,得其样本频率分布直方图如图所示. 的值;
的值;
(2)估计已购买该品牌汽车的消费群体对购车补贴金额的心理预期值的平均数(同一组数据用该区间的中点值作代表)和中位数;(精确到0.01)
(3)现在要从购车补贴金额的心理预期值在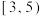 间用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行调查,求抽到2人中购车补贴金额的心理预期值都在
间用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行调查,求抽到2人中购车补贴金额的心理预期值都在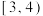 间的概率.
间的概率.
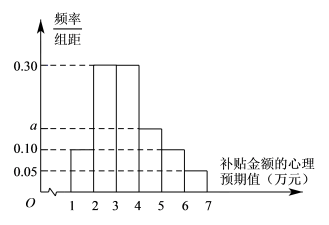
 的值;
的值;(2)估计已购买该品牌汽车的消费群体对购车补贴金额的心理预期值的平均数(同一组数据用该区间的中点值作代表)和中位数;(精确到0.01)
(3)现在要从购车补贴金额的心理预期值在
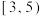 间用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行调查,求抽到2人中购车补贴金额的心理预期值都在
间用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行调查,求抽到2人中购车补贴金额的心理预期值都在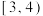 间的概率.
间的概率.
您最近半年使用:0次
2022-08-06更新
|
892次组卷
|
11卷引用:河南省名校联盟2022-2023学年高三上学期摸底联考文科数学试题
河南省名校联盟2022-2023学年高三上学期摸底联考文科数学试题(已下线)第05讲 古典概型、概率的基本性质 (精讲)(已下线)高一升高二开学分班选拔考试卷(测试范围:苏教版2019必修第二册)山西省榆次第一中学校2022-2023学年高二上学期开学考试数学试题黑龙江省佳木斯市第一中学2022-2023学年高二上学期开学调研考试数学试题黑龙江省绥化市望奎县第一中学2021-2022学年高一下学期期末数学试题内蒙古阿拉善盟第一中学2022-2023学年高二上学期期末考试数学(理)试题(已下线)专题强化 统计和概率综合问题-《考点·题型·技巧》云南省临沧市民族中学2022-2023学年上学期高二第三次月考数学试题新疆伊犁州奎屯市第一高级中学2023届高三上学期12月月考文科数学试题内蒙古海拉尔第一中学2022-2023学年高三上学期第一次月考数学(文)试题
名校
10 . 某区政府组织了以“不忘初心,牢记使命”为主题的教育活动,为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n名,获得了他们一周参与主题教育活动时间(单位:h)的频率分布直方图如图所示,已知参与主题教育活动时间在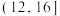 内的人数为92.
内的人数为92.
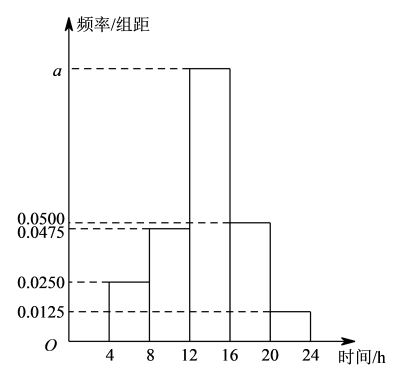
(1)求n的值;
(2)以每组数据所在区间的中点值作为本组的代表,估算这些党员干部参与主题教育活动时间的中位数(中位数精确到0.01).
(3)如果计划对参与主题教育活动时间在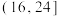 内的党员干部给予奖励,且在
内的党员干部给予奖励,且在 ,
,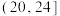 内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
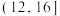 内的人数为92.
内的人数为92.
(1)求n的值;
(2)以每组数据所在区间的中点值作为本组的代表,估算这些党员干部参与主题教育活动时间的中位数(中位数精确到0.01).
(3)如果计划对参与主题教育活动时间在
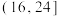 内的党员干部给予奖励,且在
内的党员干部给予奖励,且在 ,
,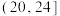 内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
您最近半年使用:0次
2022-06-27更新
|
644次组卷
|
5卷引用:江苏省常州市新桥高级中学等八校2021-2022学年高一下学期期末联考数学试题
江苏省常州市新桥高级中学等八校2021-2022学年高一下学期期末联考数学试题(已下线)知识点 用样本估计总体 易错点1 统计用表中概念不清、识图不准致误(已下线)6.1 抽样方法及特征数(精讲)浙江省杭州市桐庐中学2022-2023学年高二上学期第一次阶段性测试数学试题湖北省十堰市天河英才高中2022-2023学年高二上学期期中数学试题



