名校
解题方法
1 . 已知向量 ,
,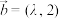 ,若
,若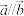 ,则
,则 ( )
( )
 ,
,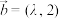 ,若
,若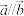 ,则
,则 ( )
( )A. | B. | C.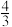 | D.3 |
您最近一年使用:0次
2024-01-25更新
|
728次组卷
|
3卷引用:浙江省宁波市慈溪市2024届高三上学期期末测试数学试题
浙江省宁波市慈溪市2024届高三上学期期末测试数学试题(已下线)第八章 平面向量(知识归纳+题型突破)(2)-单元速记·巧练(沪教版2020必修第二册)广东省广州市玉岩中学2023~2024学年高一下学期期中考试数学试卷
名校
解题方法
2 . 在四边形 中,对角线
中,对角线 与
与 交于点
交于点 ,若
,若 ,则四边形
,则四边形 一定是( )
一定是( )
 中,对角线
中,对角线 与
与 交于点
交于点 ,若
,若 ,则四边形
,则四边形 一定是( )
一定是( )| A.矩形 | B.梯形 | C.平行四边形 | D.菱形 |
您最近一年使用:0次
2024-06-08更新
|
436次组卷
|
3卷引用:温州人文高级中学2023-2024学年高一年级下学期5月月考数学试题
2023高二下·浙江·学业考试
解题方法
3 . 已知平面向量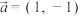 ,
,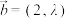 ,若
,若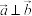 ,则实数
,则实数 ( )
( )
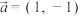 ,
,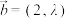 ,若
,若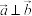 ,则实数
,则实数 ( )
( )| A.2 | B. | C.1 | D. |
您最近一年使用:0次
名校
4 . 数学里有一种证明方法叫做Proofwithoutwords,也被称为无字证明,是指仅用图象而无需文字解释就能不证自明的数学命题,由于这种证明方法的特殊性,无字证明被认为比严格的数学证明更为优雅与有条理.如下图,点 为半圆
为半圆 上一点,
上一点, ,垂足为
,垂足为 ,记
,记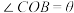 ,则由
,则由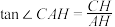 可以直接证明的三角函数公式是( )
可以直接证明的三角函数公式是( )
 为半圆
为半圆 上一点,
上一点, ,垂足为
,垂足为 ,记
,记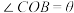 ,则由
,则由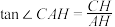 可以直接证明的三角函数公式是( )
可以直接证明的三角函数公式是( )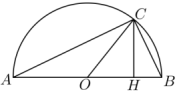
A. | B. | C. | D.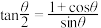 |
您最近一年使用:0次
2024-04-11更新
|
329次组卷
|
9卷引用:浙江省金丽衢十二校2023届高三下学期第二次联考数学试题
浙江省金丽衢十二校2023届高三下学期第二次联考数学试题山东省济南市山东师大附中2022-2023学年高一下学期数学竞赛选拔(初赛)试题(已下线)考点11 倍(半)角公式及其应用 --2024届高考数学考点总动员【讲】江西省南昌市第十九中学2022-2023学年高一下学期5月月考数学试卷(已下线)情境15 二级结论命题(已下线)专题02 三角恒等变换(2)-期末考点大串讲(苏教版(2019))山东省济南市历城第二中学2023-2024学年高三下学期6月高考打靶考试数学试题福建省福州市第四十中学2023-2024学年高二下学期期末考试数学试卷(已下线)考点40 三角恒等变换公式的综合应用 --高考数学100个黄金考点(2025届)【讲】
5 . 已知扇形的圆心角为2弧度,且圆心角所对的弦长为4,则该扇形的面积为( )
A. | B.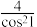 | C.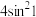 | D.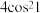 |
您最近一年使用:0次
2023-12-31更新
|
1211次组卷
|
6卷引用:浙江省温州市温州中学2023-2024学年高一上学期阶段性测试(12月月考)数学试题
浙江省温州市温州中学2023-2024学年高一上学期阶段性测试(12月月考)数学试题(已下线)专题05 三角函数公式及三角函数性质的综合应用 (1)-【寒假自学课】(人教A版2019)(已下线)专题07 三角函数的概念与诱导公式(1)-【寒假自学课】(苏教版2019)广东省深圳外国语学校2023-2024学年高一上学期期末考试数学试题(已下线)7.1.2 弧度制及其与角度制的换算-高一数学同步精品课堂(人教B版2019必修第三册)(已下线)7.1.2 弧度制及其与角度制的换算-【帮课堂】(人教B版2019必修第三册)
名校
解题方法
6 . 已知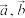 为单位向量,若
为单位向量,若 ,则
,则 ( )
( )
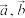 为单位向量,若
为单位向量,若 ,则
,则 ( )
( )A. | B.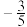 | C. | D. |
您最近一年使用:0次
2023-12-29更新
|
1206次组卷
|
9卷引用:浙江省金华第一中学2024-2025学年高三上学期10月月考数学试题
7 . 在 的范围内,与
的范围内,与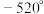 终边相同的角是( )
终边相同的角是( )
 的范围内,与
的范围内,与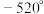 终边相同的角是( )
终边相同的角是( )A. | B.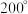 | C. | D. |
您最近一年使用:0次
解题方法
8 . 已知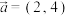 ,
,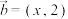 ,且
,且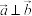 ,则
,则 的值是( )
的值是( )
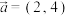 ,
,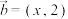 ,且
,且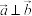 ,则
,则 的值是( )
的值是( )| A.4 | B.1 | C. | D. |
您最近一年使用:0次
2023-12-14更新
|
224次组卷
|
2卷引用:浙江省环大罗山联盟2023-2024学年高一下学期4月期中考试数学试题
23-24高一上·江苏南通·阶段练习
名校
9 . 已知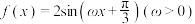 在
在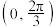 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( )
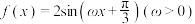 在
在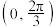 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( )A.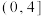 | B.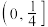 | C. | D.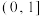 |
您最近一年使用:0次
2023-12-08更新
|
2834次组卷
|
8卷引用:浙江省杭高三校2023-2024学年高一上学期期末数学试题
浙江省杭高三校2023-2024学年高一上学期期末数学试题(已下线)江苏省南通市如皋市2023-2024学年高一上学期12月月考数学试题(已下线)7.3.1&7.3.2 三角函数的周期性、三角函数的图象与性质-【题型分类归纳】(苏教版2019必修第一册)江苏省苏州市苏州高新区第一中学教育集团2023-2024学年高一上学期12月自主学习独立作业数学试卷(已下线)专题5-3 三角函数图像与单调性、值域归类(1) - 【巅峰课堂】题型归纳与培优练(已下线)专题05 三角函数公式及三角函数性质的综合应用 (2)-【寒假自学课】(人教A版2019)山东省菏泽第一中学南京路校区2023-2024学年高一上学期1月月考数学试题(已下线)专题拓展:ω的取值范围问题-【暑假自学课】(人教A版2019必修第一册)
10 . 我国魏晋时期的数学家刘徽创造性的提出了“割圆术”,刘徽认为圆的内接正 边形随着边数
边形随着边数 的无限增大,圆的内接正
的无限增大,圆的内接正 边形的周长就无限接近圆的周长,并由此求得圆周率
边形的周长就无限接近圆的周长,并由此求得圆周率 的近似值.如图当
的近似值.如图当 时,圆内接正六边形的周长为
时,圆内接正六边形的周长为 ,故
,故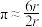 ,即
,即 .运用“割圆术”的思想,下列估算正确的是( )
.运用“割圆术”的思想,下列估算正确的是( )
 边形随着边数
边形随着边数 的无限增大,圆的内接正
的无限增大,圆的内接正 边形的周长就无限接近圆的周长,并由此求得圆周率
边形的周长就无限接近圆的周长,并由此求得圆周率 的近似值.如图当
的近似值.如图当 时,圆内接正六边形的周长为
时,圆内接正六边形的周长为 ,故
,故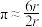 ,即
,即 .运用“割圆术”的思想,下列估算正确的是( )
.运用“割圆术”的思想,下列估算正确的是( )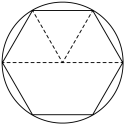
A. 时, 时, | B. 时, 时,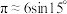 |
C. 时, 时,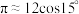 | D. 时, 时,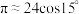 |
您最近一年使用:0次



