1 . 已知函数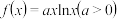 在点
在点 处的切线和直线
处的切线和直线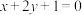 垂直.
垂直.
 求a的值;
求a的值;
 对于任意的
对于任意的 ,证明:
,证明: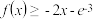 ;
;
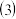 若
若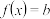 有两个实根
有两个实根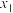 ,
,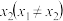 ,求证:
,求证: .
.
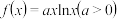 在点
在点 处的切线和直线
处的切线和直线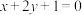 垂直.
垂直. 求a的值;
求a的值; 对于任意的
对于任意的 ,证明:
,证明: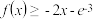 ;
;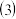 若
若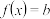 有两个实根
有两个实根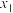 ,
,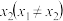 ,求证:
,求证: .
.
您最近一年使用:0次
名校
2 . 设函数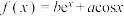 ,
, ,曲线
,曲线 在点
在点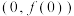 处的切线方程为
处的切线方程为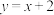 .
.
(1)求 的值;
的值;
(2)求证:方程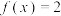 仅有一个实根;
仅有一个实根;
(3)对任意 ,有
,有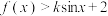 ,求正数
,求正数 的取值范围.
的取值范围.
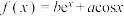 ,
, ,曲线
,曲线 在点
在点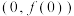 处的切线方程为
处的切线方程为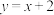 .
.(1)求
 的值;
的值;(2)求证:方程
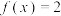 仅有一个实根;
仅有一个实根;(3)对任意
 ,有
,有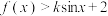 ,求正数
,求正数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
3 . 已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)当 时,判断函数
时,判断函数 在区间
在区间 上的单调性;
上的单调性;
(2)令 ,若函数
,若函数 在区间
在区间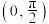 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;
(3)求证:当 时,
时, .
.
 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)当
 时,判断函数
时,判断函数 在区间
在区间 上的单调性;
上的单调性;(2)令
 ,若函数
,若函数 在区间
在区间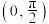 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围;(3)求证:当
 时,
时, .
.
您最近一年使用:0次
4 . 如图所示,已知椭圆 :
: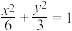 与直线
与直线 :
: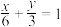 .点
.点 在直线
在直线 上,由点
上,由点 引椭圆
引椭圆 的两条切线
的两条切线 、
、 ,A、B为切点,
,A、B为切点, 是坐标原点.
是坐标原点.
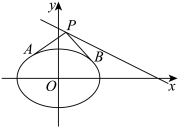
(1)若点 为直线
为直线 与
与 轴的交点,求
轴的交点,求 的面积
的面积 ;
;
(2)若 ,
, 为垂足,求证:存在定点
为垂足,求证:存在定点 ,使得
,使得 为定值.(注:椭圆
为定值.(注:椭圆 在其上一点处
在其上一点处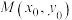 的切线方程为
的切线方程为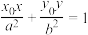 )
)
 :
: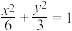 与直线
与直线 :
: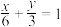 .点
.点 在直线
在直线 上,由点
上,由点 引椭圆
引椭圆 的两条切线
的两条切线 、
、 ,A、B为切点,
,A、B为切点, 是坐标原点.
是坐标原点.
(1)若点
 为直线
为直线 与
与 轴的交点,求
轴的交点,求 的面积
的面积 ;
;(2)若
 ,
, 为垂足,求证:存在定点
为垂足,求证:存在定点 ,使得
,使得 为定值.(注:椭圆
为定值.(注:椭圆 在其上一点处
在其上一点处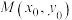 的切线方程为
的切线方程为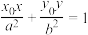 )
)
您最近一年使用:0次
解题方法
5 . 已知椭圆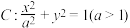 的上顶点为
的上顶点为 ,左焦点为
,左焦点为 ,直线
,直线 与圆
与圆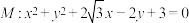 相切.
相切.
(1)求椭圆 的标准方程;
的标准方程;
(2)若不过点 的动直线
的动直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若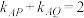 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
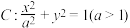 的上顶点为
的上顶点为 ,左焦点为
,左焦点为 ,直线
,直线 与圆
与圆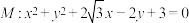 相切.
相切.(1)求椭圆
 的标准方程;
的标准方程;(2)若不过点
 的动直线
的动直线 与椭圆相交于
与椭圆相交于 两点,若
两点,若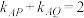 ,求证:直线
,求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
您最近一年使用:0次
6 . 已知函数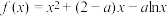 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若函数 有两个零点
有两个零点 和
和 ,求证:
,求证: 在
在 处的切线斜率恒为正数.
处的切线斜率恒为正数.
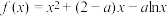 .
.(1)讨论函数
 的单调性;
的单调性;(2)若函数
 有两个零点
有两个零点 和
和 ,求证:
,求证: 在
在 处的切线斜率恒为正数.
处的切线斜率恒为正数.
您最近一年使用:0次
名校
解题方法
7 . 已知椭圆 的左右顶点为A、B,右焦点为F,C为短轴一端点,
的左右顶点为A、B,右焦点为F,C为短轴一端点, 的面积为
的面积为 ,离心率为
,离心率为 .
.
(2)过点F的直线交椭圆于M,N两点(异于A,B),直线AM与BN的交点为Q.
①求证:Q点在定直线上;
②求证:射线FQ平分∠MFB.
您最近一年使用:0次
2022-12-15更新
|
1254次组卷
|
7卷引用:山东省德州市第一中学2022-2023学年高二上学期1月期末数学试题
山东省德州市第一中学2022-2023学年高二上学期1月期末数学试题福建省厦门外国语学校石狮分校2022-2023学年高二上学期期中考试数学试题新疆生产建设兵团第六师五家渠高级中学2022-2023学年高二下学期开学考试数学试题(已下线)第五篇 向量与几何 专题11 圆锥曲线中的蝴蝶定理 微点1 圆锥曲线中的蝴蝶定理陕西省西安市西航一中2022-2023学年高二上学期期中数学试题(已下线)专题14 圆锥曲线中的蝴蝶模型(高三压轴题)(已下线)专题14 圆锥曲线中的蝴蝶模型(高三压轴题)【讲】
名校
8 . 设函数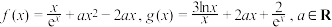 .
.
(1)讨论 的单调性;
的单调性;
(2)若 ,求证:
,求证: .
.
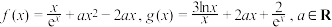 .
.(1)讨论
 的单调性;
的单调性;(2)若
 ,求证:
,求证: .
.
您最近一年使用:0次
2022-05-26更新
|
1033次组卷
|
7卷引用:山东省德州市禹城市综合高中2023-2024学年高三上学期10月月考数学试题
名校
解题方法
9 . 设函数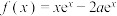 ,
,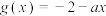 ,
, .
.
(1) 时,求
时,求 在
在 处切线方程;
处切线方程;
(2)若在y轴右侧,函数 图象恒不在函数
图象恒不在函数 的图象下方,求实数a的取值范围;
的图象下方,求实数a的取值范围;
(3)证明:当 时,
时, .
.
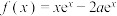 ,
,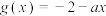 ,
, .
.(1)
 时,求
时,求 在
在 处切线方程;
处切线方程;(2)若在y轴右侧,函数
 图象恒不在函数
图象恒不在函数 的图象下方,求实数a的取值范围;
的图象下方,求实数a的取值范围;(3)证明:当
 时,
时, .
.
您最近一年使用:0次
2023-06-25更新
|
304次组卷
|
3卷引用:山东省德州市第一中学2022-2023学年高二下学期6月月考数学试题
名校
10 . 已知函数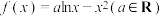 .
.
(1)讨论 的单调性;
的单调性;
(2)当 时,证明:不等式
时,证明:不等式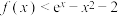 恒成立.
恒成立.
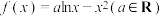 .
.(1)讨论
 的单调性;
的单调性;(2)当
 时,证明:不等式
时,证明:不等式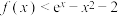 恒成立.
恒成立.
您最近一年使用:0次
2023-06-20更新
|
749次组卷
|
6卷引用:山东省德州市第一中学2022-2023学年高二下学期期末数学试题



