解题方法
1 . 设 为正整数,如果表达式
为正整数,如果表达式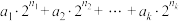 同时满足下列性质,则称之为“交错和”.①
同时满足下列性质,则称之为“交错和”.①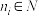 ,
,
 ;②
;②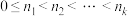 ;③当
;③当 时,
时,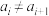 (
(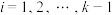 );④规定:当
);④规定:当 时,
时,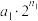 也是“交错和”.
也是“交错和”.
(1)请将7和10表示为“交错和”;
(2)若正整数 可以表示为“交错和”
可以表示为“交错和”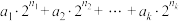 ,求证:
,求证: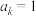 ;
;
(3)对于任意正整数 ,判断
,判断 一共有几种“交错和”的表示方法,并证明你的结论.
一共有几种“交错和”的表示方法,并证明你的结论.
 为正整数,如果表达式
为正整数,如果表达式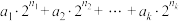 同时满足下列性质,则称之为“交错和”.①
同时满足下列性质,则称之为“交错和”.①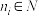 ,
,
 ;②
;②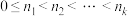 ;③当
;③当 时,
时,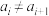 (
(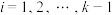 );④规定:当
);④规定:当 时,
时,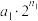 也是“交错和”.
也是“交错和”.(1)请将7和10表示为“交错和”;
(2)若正整数
 可以表示为“交错和”
可以表示为“交错和”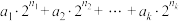 ,求证:
,求证: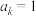 ;
;(3)对于任意正整数
 ,判断
,判断 一共有几种“交错和”的表示方法,并证明你的结论.
一共有几种“交错和”的表示方法,并证明你的结论.
您最近一年使用:0次
名校
2 . 用反证法证明命题①:“已知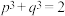 ,求证:
,求证: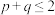 ”时,可假设“
”时,可假设“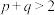 ”;命题②:“若
”;命题②:“若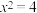 ,则
,则 或
或 ”时,可假设“
”时,可假设“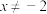 或
或 ”.以下结论正确的是
”.以下结论正确的是
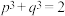 ,求证:
,求证: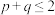 ”时,可假设“
”时,可假设“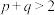 ”;命题②:“若
”;命题②:“若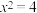 ,则
,则 或
或 ”时,可假设“
”时,可假设“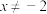 或
或 ”.以下结论正确的是
”.以下结论正确的是| A.①与②的假设都错误 | B.①与②的假设都正确 |
| C.①的假设正确,②的假设错误 | D.①的假设错误,②的假设正确 |
您最近一年使用:0次
2018-07-12更新
|
768次组卷
|
9卷引用:黑龙江省大庆实验中学2021届高三得分训练(二)数学(理)试题
黑龙江省大庆实验中学2021届高三得分训练(二)数学(理)试题安徽省宣城市郎溪中学2020-2021学年高二下学期第一次月考理科数学试题四川省仁寿第一中学校北校区2020-2021学年高二6月期末数学(文)试题广西河池市九校2020-2021学年高二下学期第二次联考数学(理)试题【全国市级联考】福建省三明市2017-2018学年高二下学期期末考试数学(文)试题湖北省咸宁市2018-2019学年高二下学期期末数学(文)试题(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)数学(上海B卷)河南省灵宝市第五高级中学2021-2022学年高二下学期第一次月考数学文科试题
名校
3 . 某班数学课代表给全班同学们出了一道证明题.甲和丁均说自己不会证明;乙说:丙会证明;丙说:丁会证明.已知四名同学中只有一人会证明此题,且只有一人说了真话.据此可以判定能证明此题的人是( )
| A.甲 | B.乙 | C.丙 | D.丁 |
您最近一年使用:0次
2021-05-06更新
|
1034次组卷
|
10卷引用:江苏省淮安市2021届高三下学期4月第二次适应性考试数学试题
江苏省淮安市2021届高三下学期4月第二次适应性考试数学试题陕西省咸阳市2021届高三五月数学信息专递试题(已下线)第2章 章末复习课(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)安徽省安庆市第十中学2020-2021学年高二下学期5月月考文科数学试题(已下线)第2章 章末复习课(基础练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-2)陕西省西安市第八十九中学2021-2022学年高二上学期第二次月考理科数学试题江苏省泰州市泰兴市第一高级中学2022届高三下学期阶段测试二数学试题新疆昌吉州行知学校2021-2022学年高二下学期期末考试数学(文)试题广西钦州市第四中学2021-2022学年高二下学期3月月考数学试题(理科)青海省海南藏族自治州高级中学2022-2023学年高二下学期期末考试数学(文)试题
名校
4 . 用反证法证明命题:“若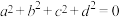 ,则
,则 ,
, ,
, ,
, 都为0”.下列假设中正确的是( )
都为0”.下列假设中正确的是( )
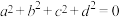 ,则
,则 ,
, ,
, ,
, 都为0”.下列假设中正确的是( )
都为0”.下列假设中正确的是( )A.假设 , , , , , , 都不为0 都不为0 | B.假设 , , , , , , 至多有一个为0 至多有一个为0 |
C.假设 , , , , , , 不都为0 不都为0 | D.假设 , , , , , , 至少有两个为0 至少有两个为0 |
您最近一年使用:0次
2021-09-17更新
|
440次组卷
|
2卷引用:黑龙江省大庆市肇州县2021届高三下学期二校联考数学(文科) 试题
名校
5 . 观察以下式子:
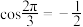 ;
;
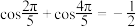 ;
;
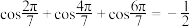 ;
;
按此规律归纳猜想第5个等式为__________ .(不需要证明)
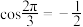 ;
;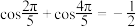 ;
;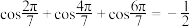 ;
;按此规律归纳猜想第5个等式为
您最近一年使用:0次
2021-05-13更新
|
626次组卷
|
4卷引用:陕西省西安中学2021届高三下学期第九次模拟考试文科数学试题
陕西省西安中学2021届高三下学期第九次模拟考试文科数学试题安徽省安庆市第十中学2020-2021学年高二下学期5月月考文科数学试题黑龙江省哈尔滨市第三十二中学2020-2021学年高二下学期期末考试理科数学试题(已下线)专题10 不等式、推理与证明、算法初步、复数-2021年高考真题和模拟题数学(文)分项汇编(全国通用)
6 . 已知集合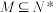 ,且
,且 中的元素个数
中的元素个数 大于等于5.若集合
大于等于5.若集合 中存在四个不同的元素
中存在四个不同的元素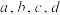 ,使得
,使得 ,则称集合
,则称集合 是“关联的”,并称集合
是“关联的”,并称集合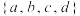 是集合
是集合 的“关联子集”;若集合
的“关联子集”;若集合 不存在“关联子集”,则称集合
不存在“关联子集”,则称集合 是“独立的”.
是“独立的”.
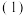 分别判断集合
分别判断集合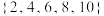 和集合
和集合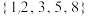 是“关联的”还是“独立的”?若是“关联的”,写出其
是“关联的”还是“独立的”?若是“关联的”,写出其所有 的关联子集;
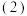 已知集合
已知集合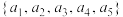 是“关联的”,且任取集合
是“关联的”,且任取集合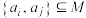 ,总存在
,总存在 的关联子集
的关联子集 ,使得
,使得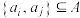 .若
.若 ,求证:
,求证: 是等差数列;
是等差数列;
 集合
集合 是“独立的”,求证:存在
是“独立的”,求证:存在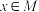 ,使得
,使得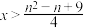 .
.
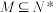 ,且
,且 中的元素个数
中的元素个数 大于等于5.若集合
大于等于5.若集合 中存在四个不同的元素
中存在四个不同的元素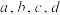 ,使得
,使得 ,则称集合
,则称集合 是“关联的”,并称集合
是“关联的”,并称集合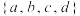 是集合
是集合 的“关联子集”;若集合
的“关联子集”;若集合 不存在“关联子集”,则称集合
不存在“关联子集”,则称集合 是“独立的”.
是“独立的”.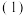 分别判断集合
分别判断集合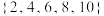 和集合
和集合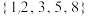 是“关联的”还是“独立的”?若是“关联的”,写出其
是“关联的”还是“独立的”?若是“关联的”,写出其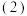 已知集合
已知集合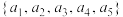 是“关联的”,且任取集合
是“关联的”,且任取集合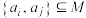 ,总存在
,总存在 的关联子集
的关联子集 ,使得
,使得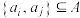 .若
.若 ,求证:
,求证: 是等差数列;
是等差数列; 集合
集合 是“独立的”,求证:存在
是“独立的”,求证:存在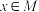 ,使得
,使得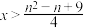 .
.
您最近一年使用:0次
2020-02-09更新
|
1826次组卷
|
10卷引用:北京市海淀区2021届高三模拟试题(一)
北京市海淀区2021届高三模拟试题(一)(已下线)考点47 推理与证明-备战2022年高考数学(文)一轮复习考点帮上海市上海中学2022届高三下学期高考模拟3数学试题北京市朝阳区中国人民大学朝阳分校2021-2022学年高三上学期开学考数学试题2020届北京市海淀区高三上学期期中数学试题(已下线)专题02 拿高分题目强化卷(第三篇)-备战2021年新高考数学分层强化训练(北京专版)北京市清华大学附属中学朝阳学校2021-2022学年高二5月月考数学试题北京市第五十七中学2021-2022学年高二下学期期末考试数学试题北京市第八中学2023届高三上学期12月测试数学试题北京市日坛中学2023-2024学年高二下学期第三次月考(6月)数学试卷
7 . 勾股定理是一个基本的几何定理,中国《周髀算经》记载了勾股定理的公式与证明.相传是在商代由商高发现,故又有称之为商高定理.我国古代称短直角边为“勾”,长直角边为“股”,斜边为“弦”.西方文献中一直把勾股定理称作毕达哥拉斯定理.毕达哥拉斯学派研究了勾为奇数、弦与股长相差为1的勾股数:如3,4,5;5,12,13;7,24,25;9,40,41;……,如设勾为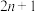 (
( ),则弦为( )
),则弦为( )
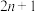 (
( ),则弦为( )
),则弦为( )A.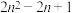 | B. | C. | D.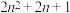 |
您最近一年使用:0次
2021-04-29更新
|
546次组卷
|
5卷引用:江西省临川第一中学暨临川一中实验学校2021届高三三模数学(理)试题
江西省临川第一中学暨临川一中实验学校2021届高三三模数学(理)试题慕华优策联考2021届高三第三次联考文科数学试卷慕华优策联考2021届高三第三次联考理科数学试卷(已下线)第2章 章末复习课(重点练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-2)(已下线)专题10 推理与证明小题大做-备战2022年高考数学冲刺横向强化精练精讲



